基于圈图Harary指数减小的图变换
2018-03-01邵燕灵
刘 奇,邵燕灵,胡 鹏
(中北大学 理学院, 太原 030051)
1 背景

设图G是(简单)连通图,V(G),E(G)分别是它的顶点集和边集,|V(G)|表示图G的阶,dG(v)表示顶点v的度,其中度为1的点称为悬挂点,与悬挂点相连的边称为悬挂边,dG(u,v)表示顶点u,v之间的距离,即u,v两点之间的最短路的长度。图G的围长指图G中所有圈的最小圈长。
设图G是n阶连通图,图G的Harary指数被定义为:
(1)
如果用γ(G,k) 表示图G中距离为k的顶点对的数量,则
(2)
用HG(v)表示图G中顶点v与其他点的距离的倒数之和,称HG(v)为顶点v的Harary指数,则
(3)
k圈图是指具有n个顶点和n-1+k条边的连通图,用μk(n)表示全体n阶k圈图的集合。用T(n)表示全体n阶树的集合,Pn、Sn、Cn分别表示n阶的路、星图、圈。
本文为了更有效地研究圈图的Harary指数变化和极值,在基于圈图的Harary指数减小的方向上,提出了5种有效的图变换,以三圈图为例,运用图变换快捷地推出了它们的Harary指数极小图,并在一定的观察基础上,对k圈图的Harary指数极小图作出猜测。
2 引理
引理1[2]设G∈T(n),n≥2,则图G的Harary指数满足
(4)
引理2[9]n阶圈Cn的Harary指数为
(5)
设G1,G2分别是m1,m2阶连通图,x∈V(G1),y∈V(G2),将顶点x,y合并为一个顶点v得到的m1+m2-1阶图记为G=G1vG2。
引理3[3]设G=G1vG2,则
(6)
设G1,G2,G3分别是m1,m2,m3阶连通图,x∈V(G1),y1,y2∈V(G2)且y1≠y2,z∈V(G3),将顶点x,y1合并为一个顶点u,顶点y2,z合并为一个顶点v,得到的m1+m2+m3-2阶图记为G=G1uG2vG3。
引理4 设G=G1uG2vG3,结合引理3,有
引理5[13]设Un,g,k是一个围长为g的n阶单圈图,圈上某一点连接k条悬挂路,其长度分别为n1,n2,…,nk,记n1≥n2≥…≥nk,若g≤2n1,则
H(Un,g,k)≤H(Un,g+1,k)
(7)
引理6[5]设G∈μ1(n),则
(8)
3 5种基本图变换
3.1 变换1:悬挂树变换
设G是一个圈图,其中v0是G中某个圈上的点,T是G中以v0为根点的一颗m阶悬挂树。将m阶悬挂树T变成一条以v0为一个端点的m阶悬挂路P,得到的图记为G′,称G′是由G经过悬挂树变换得到的图,见图1。
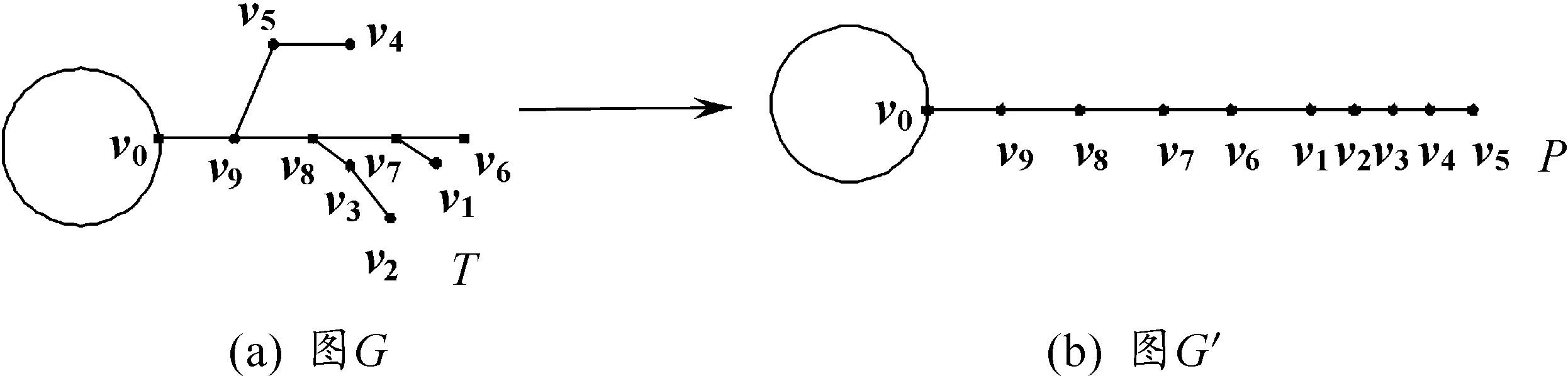
图1 悬挂树变换
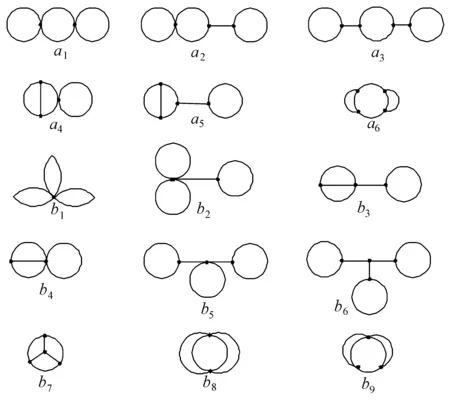
引理7 设G′是由G经过悬挂树变换得到的图,则H(G′) 证明设G0是由图G去掉T的所有边和除v0之外的所有顶点后剩余的图,则G=G0v0T,G′=G0v0P。由引理1,H(P)≤H(T),又显然 故对任意x∈V(G0)v0,有 从而由引理3可知 < 证明完毕。 3.2.1 单圈图 设G是一个n阶单圈图,C是G中的简单圈,vi0∈V(C),i=1,2,…,k,Pli=vi0vi1…vili是G中以vi0为一个端点的li阶悬挂路,i=1,2,…,k。将G中的全部悬挂路Pli融合成一条悬挂路,长度为l1+l2+…+lk,记得到的n阶图为G′,称G′是由G经过融悬挂路变换得到的图,如图2所示。 图2 单圈图 3.2.2 多圈图 设G是一个如图3所示的n阶圈图,其中G1,G3为连通图,Cm是G中一个长为m的简单圈,Pli是圈Cm上的li阶悬挂路,i=1,2,…,k。G1,G3与Cm至多有两个交点。将Cm上的全部悬挂路Pli融合成一条悬挂路,长度为l1+l2+…+lk,端点为Cm上一点v0,满足H(v0)≤H(vi),vi∈V(Cm)。记得到的n阶图为G′,称G′是由G经过融悬挂路变换得到的图,如图3所示。 图3 一般形式 引理8 设G′是由G经过融悬挂路变换得到的图,则H(G′) 证明考虑图2的情形: 记mij=d(vi0vj0),比较li与mi,i-1,mi,i+1的大小,分两步移动悬挂路: 第1步mi,i+1≤li(或mi,i-1≤li),将悬挂路Pli+1(或Pli-1)移至Pli上。 以i=1,m12≤l1为例,图G1是将图G中悬挂路Pl2移至Pl1上所得的图。 dG1(uv2i)-dG(uv2i)=dG1(uv1l1)-dG(uv20)=dG1(uv10)+l1-dG(uv20)= l1-(dG(uv20)-dG1(uv10))≥l1-(dG(uv10)+dG1(uv20))=l1-m12≥0 类似可证,若mi,i-1≤li,图G1是将图G中悬挂路Pli-1移至Pli上所得的图,则H(G1)≤H(G)。 第2步若尚未得到图G′,此时mi, i+1≥li且mi, i+1≥li+1。将G中的悬挂路Pl2移至Pl1上,所得图G2的Harary指数减小,重复可得G′。 设图G2由图G1中悬挂路Pl2移至Pl1上所得。 将图G1上悬挂路Pl2以外的顶点分成3部分: 3)Pl2与其他悬挂路V(Pli),i≥2: 当m2i≤m1i时,显然有Pl2与Pli之间点对的反距离减小; 当m2i>m1i时,有m1i>m1(i+1),Pl2与Pli之间点对的反距离增大, 以上3部分结合引理4有 从而H(G2)≤H(G1)。多次重复上述步骤后得到图G′,即H(G′)≤H(G)。 考虑图3的情形,根据前面的证明,只需要考虑变换前后悬挂路Pli与G1,G3中点的Harary指数变化。对于悬挂路Pl1,圈Cm上一点v0,满足H(v0)≤H(vi),vi∈V(Cm),使得Pl1的端点在v0处时有 (HG′(pl1)-HG2′(pl1))-(HG(pl1)-HG2(pl1))≤0 同理,悬挂路Pl2移动到Pl1的末端点时 (HG′(pl2)-HG2′(pl2))-(HG(pl2)-HG2(pl2))≤0 显然可以得出 即H(G′)≤H(G)。证毕。 设G1,G2,G3为连通图,G2的阶为m,圈长为g(g≥4),且至多有一条悬挂路,图G2与G1,G3分别有一个公共点u,v(G1,G3可为空图),G=G1uG2vG3。将G2变为由一个3长圈连接一条m-3长悬挂路构成的m阶单圈图G2′,其中点v为G2′的悬挂点,点u为G2′中3长圈的一个2度点,记G′=G1uG2′vG3,称G′是由G经过圈长变换得到的图,如图4所示。 引理9 设G′是由G经过圈长变换得到的图,则H(G′)≤H(G)。 证明考虑(a)类、(b)类的证明同理。 图G′=G1uG2′vG3由G=G1uG2vG3经过圈长变换得到。由引理6有 从而H(G2′)-H(G2)<0。由引理4可知 由dG2′(u,v)=m-2>dG2(u,v),dG2′(u,x)≥dG2(u,x),dG2′(x,v)≥dG2(x,v)(x∈V(G2)),结合引理1和引理2、3知上式中各行的值为负,可得出H(G′)-H(G)<0。证毕。 图4 圈长变换 3.4.1 双圈合边 设G=G1uG2vG3是一个n阶圈图,其中G2是一个m阶双圈图(如图5),圈Cg1与Cg2有k+1个公共点v10,…,v1k(k≥1),每个圈上至多有一条悬挂路。若k=1,合边不变,将圈Cg1,Cg2的圈长缩小至g1′=g2′=3,两圈上其他点形成悬挂路Pl1,Pl2,端点分别在两圈的非公共顶点上,得到G2′,记G′=G1uG2′vG3,称G′是由G经过去合边变换得到的图。 若k≥2,将圈Cg1,Cg2的圈长缩小至g1′=g2′=3,其余(g1+g2-k-5)个顶点放在两圈之间构成一条连接两圈的路,得到G2′,记G′=G1uG2′vG3,称G′是由G经过去合边变换得到的图。 图5 双圈合边 3.4.2 三圈合边 三圈合边的情形分为以下4类(见图6): 图6 三圈合边 引理10 设G′是由G经过去合边变换得到的图,则H(G′)≤H(G)。 证明双圈合边: 当k=1时,可根据圈长变换证明。 当k≥2时,图G经过去合边变换得到图G′,结合引理3,G2的Harary指数的变化可看做两部分。 1) 圈Cg1上的点对应圈Cg2上的点对。记图G中圈Cg1、Cg2经过变换后的部分为,结合引理9中圈长变换的证明可得: 2) 圈Cg1与圈Cg2间的点对。合边v1v2上的点对变换后的距离没有变化,合边以外的点vi、vj(vi∈cg1,vj∈cg2),有 dG′(vivj)=dG′(viv10)+dG′(v10v1k)+dG′(v1kvj)≥dG(viv10)+dG(v10v1k)+dG(v1kvj)≥dG(vivj) 考虑G1、G3,任取v1∈G1,v2∈G2,v3∈G3,显然有dG′(vi,vj)≥dG(vi,vj),结合引理3的证明可得H(G′)-H(G)<0。 三圈合边: 记图G中圈C1经过变换后的部分为C1′,对于图G中圈C1上任一点v,结合引理3,有Hc1′(v)≤Hc1(v),且 对于图G中圈C3,同理可得Hc3′(v)≤Hc3(v),且 考虑弧v1v2上的内点,对于点v5,计算对比后容易得出HG2′(v3)≤HG2(v3)。对于弧v1v2上除v5以外的任一内点v,有HG2′v3(v)≤HG2v3(v),且 情形4:设G′是由G经过去合边变换得到。 记图G中路径v0v1u1、v0v2u2、v0v3u3为P1、P2、P3,经过变换后的部分为P1′、P2′、P3′。结合引理3,对于P1上u1以外的点v,有H(P1′v)≤H(P1v)且 任取v1∈P1,v2∈P2,v3∈P3,显然有dG′(vi,vj)≥dG(vi,vj)。对于图G中路径P2、P3上u2、u3以外的点v,同理可得H(P2′v)≤H(P2v),H(P3′v)≤H(P3v),且 考虑点u1、u2、u3有 同理,HG2′(u2)≤HG2(u2),HG2′(u3)≤HG2(u3)。 综上可以得出H(G2′)≤H(G2)。 此时只需证明HG′(v)≤HG(v)(任意v∈V(G)V(G2)),即可得出H(G′)≤H(G)。任取v∈V(G)V(G2),显然有HG2′(v)≤HG2(v), HG′(v)=HG1′(v)+HG2′(v)+HG3′(v)≤HG1(v)+HG2(v)+HG3(v)=HG(v) 从而H(G′)≤H(G),证毕。 设G∈μk(n),G中各圈的圈长均为g=3,各圈上至多有1条悬挂路。移动G中圈的相对位置或改变圈与圈、圈与路上点之间的距离,会改变图G的Harary指数值。 3.5.1 双圈图 设G∈μ2(n),G中两圈的圈长均为g=3,如图7(a)所示,两圈位于路径两端。移动其中一圈的位置,改变两圈结构使两圈有一条合边,其余点构成一条悬挂路,端点为一个2度点得到的图记为G′,称G′是由G经过圈结构变换得到的图。 3.5.2 三圈图 图7 移圈变换 引理11 设G′是由G经过移圈变换得到的图,则H(G′)≤H(G)。 证明两种情形证明过程类似,考虑(a)类。 设G是一个如图7所示的双圈图,G′是由G经过变换5得到。考虑到变换前后只有一个点v0的Harary指数改变,则有 证毕。 定理1 设G∈μ3(n),图G经过上述5种变换后可得到如图8中G1所示的极小Harary指数图。 图8 G1 图G1的Harary指数为 证明根据文献[12],三圈图中圈与圈的结构形式见图9,其中,图a1~a6经过前,种变换后能得到相似结构的图,如图10所示。 图9 三圈图中圈与圈的结构形式 图10 经过前,种变换后得到的相似结构的图 以a1、a5为例,变换得到的结构图见图11。 图11 a1,a5变换实例 图b1~b9经过5种变换后能得到相似结构的图,如图12所示。 图12 b1~b9变换实例 以b1、b9为例,变换得到的结构图见图13。 图13 b1、b9变换实例 对Ga和Gb继续做圈结构变换可推出三圈图的极小Harary指数图G1,见图14。 图14 三圈图的极小Harary指数图 证毕。 双圈图的极小Harary指数图运用上述图变换推出所得极图如下: 图15 极图示例 观察单圈、双圈与三圈图的极小Harary指数图发现:当n较大时,圈的围长都是最终缩小至g=3,之后关于圈的相对位置进行组合使得图的直径尽可能大,故而猜测阶为n、边数为m的连通多圈图的极小Harary指数图为所有诱导圈的长度为3且直径最大的图。 [2] GUTMAN I.A property of the Wiener number and its modifications[J].Indian J.Chem.,1997,36A:128-132. [5] XU K,DAS K C.Extremal Unicyclic and Bicyclic Graphs with Respect to Harary Index[J].Asian Academy of Management Journal of Accounting & Finance,2013,36(2):373-383. [8] AI C,YU G,FENG L.The Harary index of trees[J].Utilitas Mathematica,2011,87(3):21-31. [9] XU K,DAS K C.On Harary index of graphs [J].Discrete Applied Mathematics,2011,159(15):1631-1640. [10] XI L F.Lipschitz equivalence of dust-like self-similar sets[J].Mathematische Zeitschrift,2010,266(3):683-691. [11] LI S,LI X,ZHU Z.On tricyclic graphs with minimal energy[J].Match Communications in Mathematical & in Computer Chemistry,2008,59(2):397-419. [12] 李小新,查淑萍,范益政.连通图的Harary指数上界及其极图[J].中国科学技术大学学报,2014,44(2):96-100. [13] 蔡改香,余桂东,邢抱花.具有k个悬挂点的n阶单圈图的Harary指数[J].华东师范大学学报(自然科学版),2015(1):120-125. [14] 邢抱花.关于双圈图的Harary指数[J].菏泽学院学报,2015(5):14-16.3.2 变换2:融悬挂路变换






3.3 变换3:圈长变换
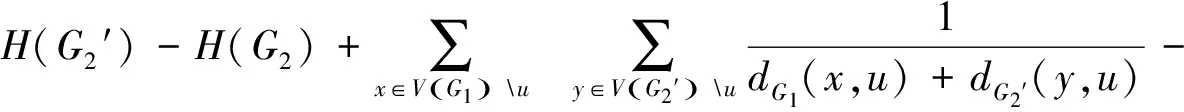

3.4 变换4:去合边变换
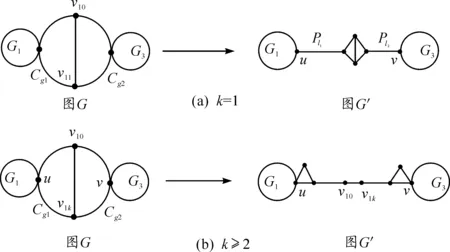

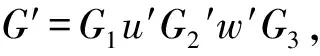
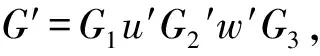
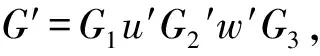
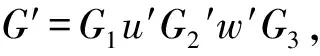





3.5 变换5:圈结构变换

4 应用



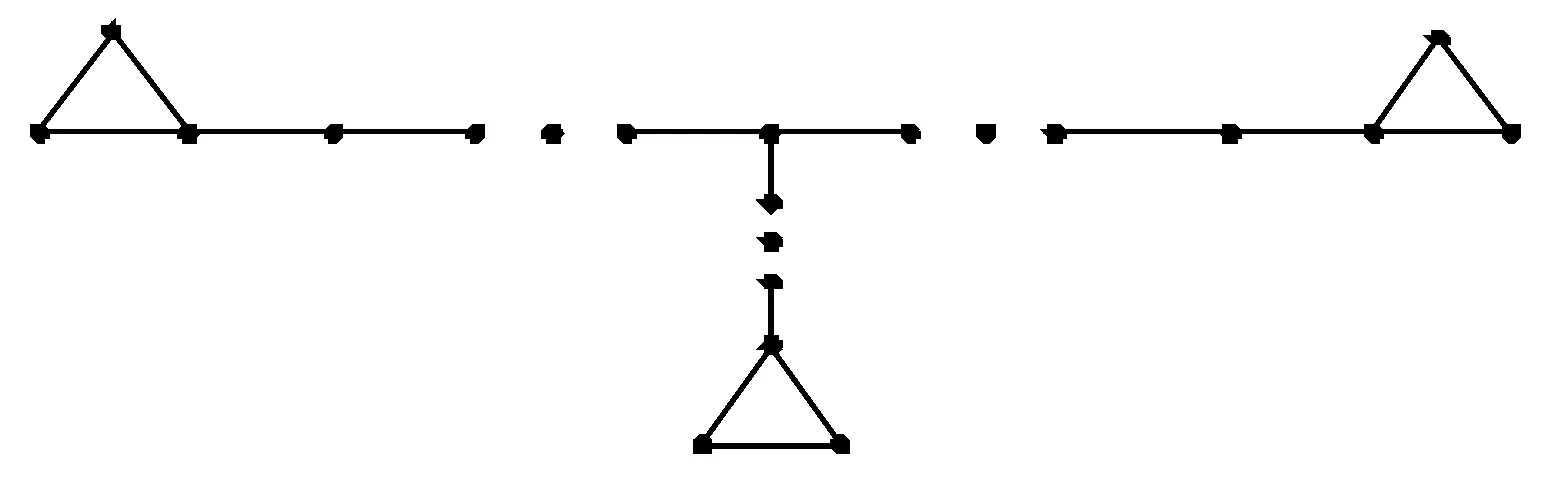


5 猜想