考虑初次感染和再次感染的丙肝模型分析

高 雁，乔志琴

(中北大学 理学院， 太原 030051)

1 背景

丙肝是由丙型肝炎病毒 (HCV) 感染所引起的疾病，其传染性很强，一旦感染很难治愈，且极易慢性化和发生肝硬化，甚至诱发肝癌。国内外至今仍没有阻止HCV感染的疫苗，故对于丙肝的传播进行研究是十分有必要的。许多学者通过生物及数学研究对丙肝进行讨论，如文献 [1] 在总人口变化的情况下，引入丙肝慢性阶段并建立年龄结构模型。文献[2] 从治疗的角度出发并指出根除丙肝疾病是困难的，它可能与遗传有关，且治愈后仍有可能再次感染。Corson.S等[3]通过建立数学模型研究HCV在 IDU中的传播，并指出基本再生数在模型中起决定性作用，当R0=1时可以看作区别两种不同结果的临界阈值。文献 [4] 指出有效治疗可以预防和控制丙肝传播速度及再次感染。Elbasha.E.H等[5]研究了再次感染与初次感染没有区别时模型的全局稳定性。

由于丙肝的恢复者只具有暂时免疫，故其可能在失去免疫或免疫存在的情况下发生再次感染。本文将失去免疫下的再感染称为初次感染，而将免疫存在下的再感染称为再次感染。再次感染较初次感染在行为上有很大的区别，如：再次感染率会减少，再次感染自发清除病毒率会增加。对丙肝传染研究的数学模型有很多，但大部分的研究过程并没有对初次感染和再次感染加以区分或者只是定性地描述两者的区别。

图1 仓室图

本文在文献 [5] 的基础上，在对初次感染和再次感染加以区别的情况下，从定量的角度利用微分方程定性与稳定性理论来进一步探究 HCV 传播过程中的动力学性态。就易感者S、初次感染者I、恢复者R、再次感染者V建立数学模型，其对应的仓室图见图1。

(1)

其中：参数Λ>0，表示人口输入率；μ>0，表示自然死亡率；d>0，表示因病死亡率；β>0，表示接触率；σ>0，表示初次感染恢复率；γ>0，表示失去免疫率；0<ψ<1，表示恢复者的相对易感率；α>1，表示再次感染者的相对恢复率；υ>0，表示再次感染者的相对传染率。

2 定理

为方便下文讨论，特给出以下定理。

定理1 若S(0)>0,I(0)>0,R(0)>0,V(0)>0是模型(1)的初始值，则在任何t>0情况下模型的解 (S(t),I(t),R(t),V(t))均为正。

证明令

t1=sup{t>0:S(t)>0,I(t)>0,R(t)>0,V(t)>0}>0

根据模型(1)的第1个等式得出：

然后可以写成

因此，

故

同理，可以得到在任何t>0情况下I(t)>0,R(t)>0,和V(t)>0，因此模型(1)的解均为正解，证毕。

证明将模型(1)中的所有等式相加，有

3 无病平衡点分析

基本再生数R0作为阈值参数，在流行病的传播过程中扮演着重要的角色。求R0的方法有很多，这里采用下一代矩阵法[6]来求模型 (1) 的基本再生数。

F(新感染项) 与H(过渡项) 分别给出如下：

根据文献 [6] 的定理2可知，基本再生数可被定义为R0=ρ(FH-1)(其中ρ表示下一代矩阵FH-1的谱半径)，故有

(2)

定理3 当R0<1时，无病平衡点E0是局部渐近稳定。

证明模型(1)在E0处的雅可比矩阵如下：

直接计算可得其对应的特征值分别为：

η1=-μ,η2=-γ-μ,η3=-ασ-μ-d,η4=β-μ-σ-d

显然，η1,η2,η3均小于零，当R0<1(即β<μ+σ+d) 时，有η4<0,从而E0局部渐近稳定；否则当R0>1时，将有η4>0，此时E0是一个鞍点。证毕。

4 地方病平衡点分析

本节主要讨论地方病平衡点 (正平衡点) 的存在性问题。

不失一般性，设E1=(S*,I*,R*,V*)是模型 (1) 的一个正平衡点。其中S*,I*,R*,V*可令模型 (1) 的右端为零并迭代得到：

(3)

(4)

(5)

σI*+ασV*-(ψλ+γ+μ)R*=0

(6)

(7)

将式(3)～(5)均代入式(6)，(7)中，整理后得到关于λ的三次方程如下：

λ(Aλ2+Bλ+C)=0

(8)

其中：

A=γψΛ(d+μ+σ)(ασ+μ+d)

B=γΛ(ασ+μ+d)(-ψυβσ+d2ψ+2dμψ-dψβ+dψσ+μ2ψ-μψβ+

μψσ+μασ+αγσ+ασ2+dμ+dγ+dσ+μ2+μγ+μσ)

C=γΛ(ασ+μ+d)2(d+μ+σ-β)(γ+μ)

事实上，正平衡点E1的存在性等价于λ的存在性。对于方程 (8)，有λ=0 或Aλ2+Bλ+C=0。而当λ=0时，E1即为无病平衡点E0，故对于正平衡点E1只需考虑等式

Aλ2+Bλ+C=0

(9)

显然，系数A恒为正，故方程 (9) 的正根 (即正平衡点E1) 的个数与C的符号有关，而C的符号由基本再生数R0决定。现将正平衡点的存在情况归结为以下定理：

定理4 正平衡点的存在性：

1) 当C<0(即R0>1) 时，系统(1)有唯一的正平衡点；

2) 当C=0且B<0或B2-4AC=0 时，系统(1)有唯一的正平衡点；

3) 当C>0(即R0<1)，B<0 且B2-4AC>0 时，系统(1)有2个正平衡点；

4) 其他情况下系统(1)没有正平衡点。

5 分支现象分析

事实上，当R0<1时，若系统 (1) 同时存在稳定的无病平衡点和稳定的正平衡点，则会出现后向分支现象。根据定理 4 中情况 3) 可知，模型 (1) 可能会产生后向分支现象。选取a和b作为分支参数来讨论系统 (1) 是否会出现分支现象。令S=x1,I=x2,R=x3,V=x4,则模型可以改写为：

(10)

这里

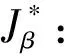
对应的特征方程为

λ4+a1λ3+a2λ2+a3λ=0

(11)

其中 ：

a1=ασ+d+3μ+γ

a2=2μασ+αγσ+2dμ+dγ+3μ2+2μγ

a3=μ(ασ+μ+d)(γ+μ)

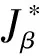
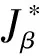
根据文献[4]中的定理4.1来分别计算后向分支系数a和b。

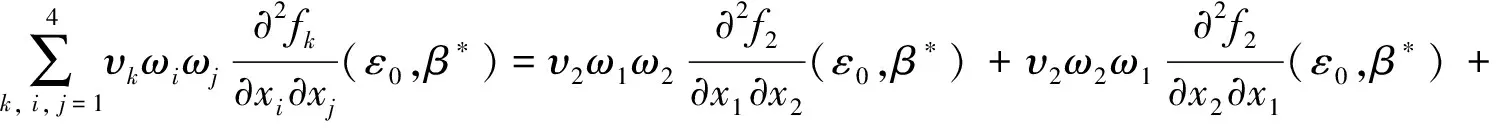
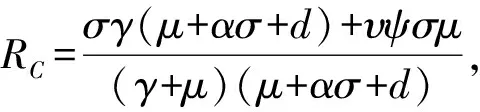
定理5 当R0=1且RC>1时，系统(1)出现后向分支。

6 结论

事实上，丙肝的恢复者并非获得终身免疫，故其可能在失去免疫或免疫存在的情况下发生第二次感染，且再次感染较初次感染在行为上有很大的区别，例如：再次感染率会减少，再次感染自发清除病毒率会增加。本文在区别初次感染和再次感染的情况下建立了一个SIRV模型，并利用微分方程定性与稳定性理论对其动力学性态进行分析和讨论。分析结果给出无病平衡点的稳定性和地方病平衡点的存在性，同时还指出：在对初次感染和再次感染加以区别考虑的情况下，当R0=1且RC>1时系统将出现后向分支，产生后向分支就意味着对传染病(比如丙肝)的控制会依赖于模型的初始数据，这对于传染病的预防和控制是不利的。接下来希望数学和生物医学研究者对如何预防和控制传染病作进一步的研究，为解决丙肝等疾病的治疗问题提出理论和实践相结合的建议。

[1] MARTCHEVA M,CASTILLO-CHAVEZ C.Diseases with chronic stage in a population with varying size[J].Mathematical Biosciences,2003,182(1)：1-25.

[2] WESTBROOK R,DUSHEIKO G.Natural history of hepatitis C virus infection[J].Journal of Hepatology,2014,61(1)：S58-S68.

[3] CORSON S,GREENHALGH D.Mathematically modelling the spread of hepatitis C in injecting drug users[J].Mathematical Medicine and Biology,2012,29(3)：205-230.

[4] DE V A S,KRETZSCHMAR M E E.Benefits of hepatitis C virus treatment:A balance of preventing onward transmission and re-infection[J].Mathematical biosciences,2014,258：11-18.

[5] ELBASHA E H.Model for hepatitis C virus transmissions[J].Mathematical biosciences and engineering,2013,10(4)：1045-1065.

[6] DRIESSCHE P V D,WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical biosciences,2002,180(1)：29-48.

[7] CASTILLO-CHAVEZ C,SONG B.Dynamical models of tuberculosis and their applications[J].Mathematical biosciences and engineering,2004,(1)：361-404.

[8] NAZARI F,GUMEL A B,ELBASHA E H.Differential characteristics of primary infection and re-infection can cause backward bifurcation in HCV transmission dynamics[J].Mathematical Biosciences,2015,263：51-69.

[9] HUANG Lu.Oral small molecule drugs for the treatment of Hepatitis C and the patent research[J].Chinese Journal of New Drugs,2016,25(10)：1095-1101.

[10] TIAN Y J.Analysis on the prevalence and case report quality of Hepatitis C,qiannan prefecture,2011—2014[J].Preventive Medical Tribune，2016.