LLC谐振变换器的分析和设计
2018-03-01高文根王金桥
徐 东,高文根,王金桥
(1.安徽工程大学 检测技术与节能装置安徽省重点实验室, 安徽 芜湖 241000;2.奇瑞新能源汽车技术有限公司, 安徽 芜湖 241000)
总体来说,开关稳压电源根据功率开关管的控制方式不同分成PWM和谐振型两种。由于开关稳压电源大频率下还要能表现出高功率密度以及高效率的性能需求,因此使得人们对谐振型变换器产生了兴趣[1]。由于在很多情况下都需要LLC谐振变换器的静态指标和动态指标以及系统的抗干扰能力满足要求,但谐振变换器运行状况复杂,传统的状态空间近似不能满足,所以合适的小信号建模方法对于系统而言重要性不言而喻[2]。文献[3]对半桥LLC建立了稳态模型以进行参数优化,但并未对动态模型进行分析。文献[4]提出了一种适用于工程使用的改进型等效电路模型,但并未给出校正和控制的设计。文献[5]分析了LLC的工作原理,但不够形象具体。本文详细分析了LLC的工作过程,直观地给出了各个器件在不同时期的开关状态,并建立了频域模型,设计了相应的控制策略。
1 LLC的工作原理
LLC变换器拓扑见图1。变压器的一次侧有MOSFET功率管Q1、Q2,其中信号Vg1、Vg2分别是驱动功率管的占空比为0.5的互补带死区的信号,电感Lr、电容Cr、电感Lm构成LLC的谐振腔,变压器的次边是全波整流和输出滤波。
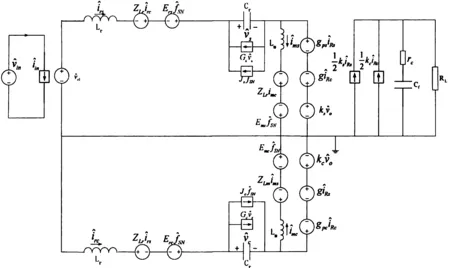
LLC拓扑结构因其运行过程的特殊性使得运行过程存在2个固有谐振频率,分别为f1、f2:
开关频率fs在f1 图1 LLC变换器拓扑 LLC变换器在单个运行周期具体可以细分成4个阶段,LLC的主要工作模态如图2所示。 阶段1:t0 功率管Q2关断,此时功率管Q1上的体寄生二极管导通。此时的开关频率小于谐振腔的固有谐振频率,谐振网络可以理解为感性负载,电流与电压的关系表现为电流滞后。驱动信号VT2从零到阈值变化,根据谐振的原理可知谐振电感Lr流过的电流为从右向左并且逐渐减小,寄生电容C1在前一个周期是上正下负,之前的电流会将电容里面存储的电荷放掉,功率管Q1两端的电压逐渐为零,谐振腔的阻抗特性和反向电流为功率管Q1的ZVS提供前提。此时Lm电压由于谐振特性表现为上正下负,能量传递到二次侧绕组,二次侧快恢复二极管D1导通,全波整流电路开始工作,输出电压为Uo,变压器匝比是定值n,所以Lm上的电压为nUo,变压器次边的输出被钳位,所以此过程Lm与谐振过程无关,因为能量在消耗所以谐振电流会逐渐减小。阶段1结束。 阶段2:t1 功率管Q1在t1时刻因驱动信号VT2导通,次边快恢复二极管D1导通,因为变压器的作用,原边被钳位在nU0,Lm充电不介入谐振过程。ILr与ILm不停增加,当ILm等于ILr时,阶段2结束。变压器一次侧绕组电流近似为零,故变压器二次侧的电流为零,快恢复二极管D1流过的电流为零,此时二极管两端的电压依然存在,使得二极管表现ZCS。 图2 LLC的主要工作模态 阶段3:t2 此时ILm与ILr相等,次边快恢复二极管关断,变压器次边没有输出,主边不再因为输出电压而被钳位,即Lm两端的电压可以变化,Lm介入谐振过程。Lr和Lm共同谐振,f1 阶段4:t3 功率管Q1、Q2关断,即功率管处于死区时间,由于ILm与ILr相当,输出仍被变压器隔离,此时谐振电感上的电流方向为从左到右并开始向Q1的寄生电容充电,向功率管Q2的寄生电容放电。当放电结束时,功率管Q2的体寄生二极管导通,在这个过程中,变压器不传递能量,系统输出只有靠电容Co提供。LLC变换器主要元器件工作模态见表1。 分析表1发现: 表1 LLC变换器主要元器件工作模态 1) 阶段1的电流方向是因谐振腔的阻抗情况导致的,感性负载才能导致电流从右向左,并将Q1的寄生电容的电荷放掉,完成零电压开通以降低开通损耗。负载的状况是开关频率决定,因此不合适的开关频率可能会使得LLC不能全负载范围ZVS。 2) 在次边二极管都关断时,变压器起着隔离作用,此时Lm会介入谐振。 3)Q1、Q2、D1截止时,Lm参与谐振,输出电压由电容Co提供,且输出没有滤波电感,所以要求Co的容值较大。 4) 阶段4的时间长短(即死区时间)是开关管ZVS能否实现的制约条件之一,合理设置死区时间也是设计的重点[6-7]。 常见的开关电源建模方法有状态空间法[5]、等效电路法[8]、扩展函数描述法[9-11]。考虑到状态空间平均法应用于谐振电路时误差较大,扩展函数描述法求解传递函数的过程复杂,所以本文使用等效电路法建立LLC的小信号模型。等效电路法的基本方法是:对于LLC中的各个元件逐个列出关系式,用近似和平衡的方法求解表达式,求出其稳态模型和小信号线性模型。每个电信号都可以理解为正弦信号与余弦信号的叠加形式: i(t)≈is(t)sinωst+ic(t)cosωst (1) v(t)≈vs(t)sinωst+vc(t)cosωst (2) 图3 电感伏安瞬时形式 电感原件的小信号模型见图3。 (3) 将式(1)(2)代入式(3)得: (4) (5) Vs=-ΩsLic,Vc=ΩsLis 图4 电感的小信号模型 同理,求出其他元器件如电容、电阻以及开关网络、全波整流电路的小信号等效电路模型,最后得到整个LLC拓扑的小信号等效电路模型,如图5所示。 图5 LLC变换器小信号数学模型 求得控制信号即开关频率—LLC输出的传递函数关系式为: (6) (7) 图6 控制系统结构 由于LLC的传递函数是0型有静差,故而要引入积分环节。PI比例积分控制实现简单,鲁棒性强,是工程实践中应用最广泛的控制器[12]。它包括比例环节和积分环节,加入PI控制可以使系统的动态过程快速、平稳、准确。PI控制器相当于在原点引进了一个极点,能够减少和控制系统的稳态误差,还能提高系统的稳态特性。 图6为闭环系统的概念图[13]。其中:Gc(s)是校正环节的频域模型;H(s)是AD采样的频域模型;Gvco(s)为PFM产生器的频域模型。在一定的条件下,可以把AD采样和PFM产生器理解为成线性系数[14-15]。 系统参数为Vin=110 V、n=4.58,Lr=27 μF,Cr=90 nF,Lm=112 μF,RL=2.4 Ω,开关频率为100 kHz,Gvco(s)=10 kHz/V,H(s)=0.2,代入式(6),可得系统传递函数: 图7 LLC系统补偿前后的伯德图 LLC系统的直流增益较小,为了闭环稳定[16]需要适当增大,开关频率的1/5~1/10应为补偿后的截止频率,故经过设计选择补偿网络的K=65,Ti=300e-6。补偿前后的伯德图如图7所示。其中,G0表示未补偿系统的伯德图,G1为补偿之后的伯德图。 在Matlab的Simulink环境下搭建仿真平台,平台内包括主电路部分、比较补偿部分、VCO部分。Simulink中没有根据电压信号不同产生不同频率的方波信号的模块,所以其中VCO部分使用Matlab中的S函数编写。S函数可以使用多种语言编写,实现连续离散信号的生成,在此之前要完成S函数的初始化,选择合适的解法器。本文使用S函数M文件的模板格式编写,大大增加了开发模块的可靠性。 对比校正补偿与开环的仿真,见图8。 图8 系统Simulink环境仿真图 仿真的输出波形如图9所示,实线为开环输出电压响应曲线,虚线为闭环输出响应曲线。图10表示在某一时刻突加负载时输出的响应曲线。从仿真结果看:系统具有很好的调节特性和稳态特性,由于PI的加入使得LLC系统的超调量减少,但牺牲了系统的反应时间。在3 ms时突加负载或突减负载,0.2 ms左右后系统稳定,证明了系统具有较强的抗干扰能力。系统良好的稳态性能和动态性能说明了数学模型的合理性和控制策略的正确性。 图9 LLC输出响应曲线 图11 突减负载响应 本文详尽说明了LLC的工作机制,直观地绘制了主要器件的开通截止状况,依据建立的数学模型,得到了LLC变换器的频域模型,并设计了保持稳定和抗扰动输出的控制方法。运用S函数设计了VCO模块,最后采用Matlab验证了VCO模块以及控制策略设计的合理性。 [1] BHUVANESWARI B C,BABU R S R.A review on LLC Resonant Converter[C] //International Conference on Computation of Power,Energy Information and Commuincation.India: IEEE,2016:620-623. [2] 徐德鸿.电力电子系统建模及控制[M].北京:机械工业出版社,2006. [3] 陈志坚,林国庆.半桥型LLC谐振变换器的建模和设计[J].电工电气,2010(5):5-8. [4] TIAN S,LEE F C,LI Q.Equivalent circuit modeling of LLC resonant converter[C]//Applied Power Electronics Conference and Exposition.[S.l.]:IEEE,2016:1608-1615. [5] 陆治国,余昌斌.新型LLC谐振变换器的分析与设计[J].电气应用,2008,27(1):65-68. [6] 张澧生.LLC谐振变换器软开关边界理论及最小死区设计[J].华东师范大学学报(自然科学版),2015,2015(6):90-100. [7] LU B,LIU W,LIANG Y,et al.Optimal design methodology for LLC resonant converter[C] // IEEE APEC 2006.USA:IEEE,2006:533-538. [9] YANG X Q.Extended describing function method for small-signal modeling of resonant and multi-resonant converters[Z].1994. [10] 张卫平.开关变换器的建模与控制[M].北京:中国电力出版社,2006. [11] CHANG C H,CHANG E C,CHENG C A,et al.Small signal modeling of LLC resonant converters based on extended describing function[C]//International Symposium on Computer,Consumer and Control.[S.l.]:IEEE Computer Society,2012:365-368. [12] 胡寿松.自动控制原理 [M].4版.北京:科学出版社,2001. [13] 程红.开关变换器建模、控制及其控制器的数字实现[M].北京:清华大学出版社,2013. [14] PARK H P,JUNG J H.Modeling and feedback control of LLC resonant converters at high switching frequency [J].Journal of Power Electronics,2016,16(3):849-860. [15] PARK H P,JUNG J H.Power stage and feedback loop design for LLC resonant converter in high switching frequency operation[J].IEEE Transactions on Power Electronics,2016(99):1-1. [16] PARK H P,JUNG J H.Improved control strategy of 1 MHz LLC converter for high frequency resolution[C]//Applied Power Electronics Conference and Exposition.[S.l.]:IEEE,2016:3213-3218.


2 LLC谐振变换器的小信号建模


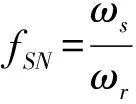
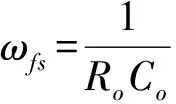
3 控制策略





4 结束语