基于正交试验设计和灰色系统理论的除雪铲优化设计

2018-03-01冯艳秋

建筑机械 2018年1期

倪坤，冯艳秋

（1. 徐工集团江苏徐州工程机械研究院，江苏徐州 221004；2. 徐州徐工铁路装备有限公司，江苏徐州 221004）

近年来，随着城市道路、高速公路、机场建设的快速发展，冬季路面积雪已成为目前交通所面临的主要问题，严重制约经济发展。目前，在我国冬季路面除雪方式主要有人工除雪、化学除雪、机械除雪3类。其中，除雪铲是应用最广、起源最早的除雪设备。由以往的试验可知，除雪铲的质量和结构强度的合理性直接影响着除雪铲的工作效率及使用寿命。

由于影响除雪铲的质量和结构强度的因素很多，利用常规的分析方法选择合理的结构参数，不仅需要大量的试验，而且分析工作繁琐、复杂，大大影响了设计效率和质量。本文利用正交试验法和灰色系统理论，研究除雪铲目标质量与各结构参数之间的关联性，得到各参数与理想目标质量之间的关联度，从而获得优化的结构参数组合。

1 除雪铲的有限元模型

1.1 除雪铲的受力分析

除雪铲在进行除雪作业时所受到的除雪阻力FP主要包括：铲刃与路面的滑动摩擦阻力Ff，分离积雪的切削阻力Fc，以及将积雪沿铲体表面抛出时雪对铲体的阻力Fa，即［1］

式中 Ff——犁刃与路面的滑动摩擦阻力；

Fc——分离积雪的切削阻力；

Fa——将积雪沿犁面抛出时雪对犁的阻力。

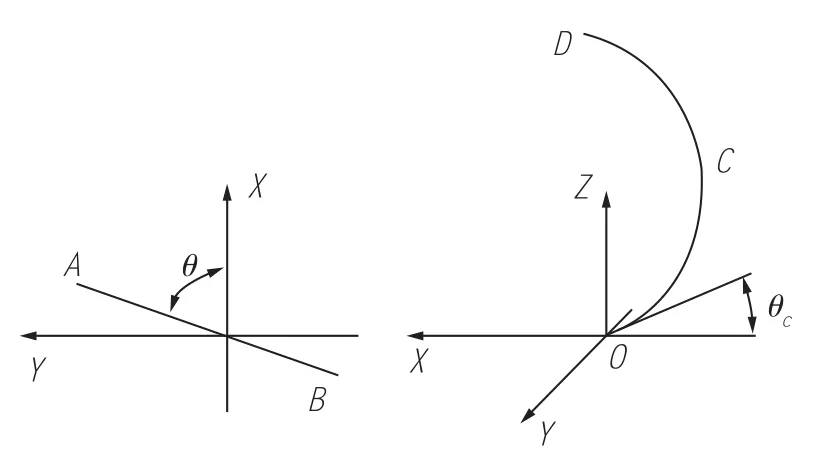
图1 铲体受力直角坐标系

为便于计算分析，建立如图1所示的铲体受力直角坐标系。定义除雪铲前进的方向为X轴正方向，铲体左侧方向为Y轴正方向，垂直向上方向为Z轴正方向。图中铲体长度方向AB与除雪铲行进方向（X轴正方向）所成的锐角θ为行进角，雪铲OCD与地面间夹角θc为切削角。除雪铲的除雪阻力FP按图1坐标系分解为前进方向分力FPx、侧向分力FPy和垂直分力FPz。

同理，按上述坐标对Ff、Fc和Fa进行分解，则有

式中 Ffx、Fcx和Fax——前进方向分力；

Fcy和Fay——侧向分力；

Fcz——垂直分力。

于是，可得除雪铲在前进方向上的阻力FPx为

侧向阻力FPy为

垂直方向阻力FPz为

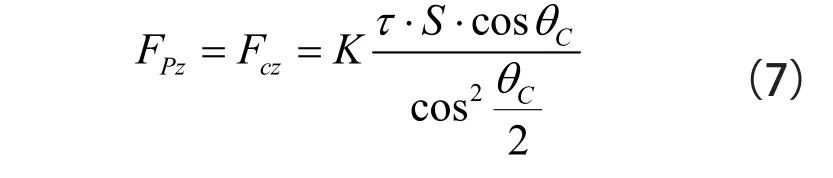
式中 μf—— 刃口与路面的摩擦系数，钢与压实雪的摩擦系数为0.1；

WP——犁体质量，kg；

H—— 雪的抗压强度,压实雪为（1.96～16.18）×106，冰层为（8.83～29.43）×106，Pa；压实雪可取9.8×106Pa；

T—— 雪的抗断应力，对于压实雪τ=0.024H+9.2×104，对于新雪τ=0，Pa；

S——除雪断面积=除雪宽×除雪深，m2；

θ——犁的行进角，°；

θc——犁的切削角，°；

υ——犁的行进速度，m/s；

ρ—— 雪的密度，kg/m3；压实雪ρ=0.45～0.75g/cm3，可取700kg/m3；

K——刃口形状系数，K=1。

1.2 除雪铲的强度分析

文章首先在CAD软件中建立了除雪铲的三维几何模型，然后导入CAE软件中进行有限元分析。在对除雪铲进行材料属性设置时，除雪铲的铲齿材料为65Mn，其余材料为Q345E。由于除雪铲结构形状较为复杂，网格划分采用智能分网与人工干预相结合的方法进行单元划分，划分网格后的除雪铲有限元模型如图2所示。图2为试验1条件下的除雪铲有限元模型，模型的节点数为52162，单元数为7494。在边界条件设置时，在除雪铲中间筋板的螺纹孔处施加固定约束，在除雪铲铲刃的前表面施加除雪阻力，除雪阻力的大小可通过式（5）、（6）、（7）计算得到，其结果分别为前进力FPx=18.378kN，侧向阻力FPy=11.914kN，垂直方向阻力FPz=11.472kN。完成以上设置后，即可对除雪铲进行强度分析，图3、图4即为试验1条件下除雪铲的变形分布图与应力分布图。

2 除雪铲的正交设计

2.1 正交试验指标

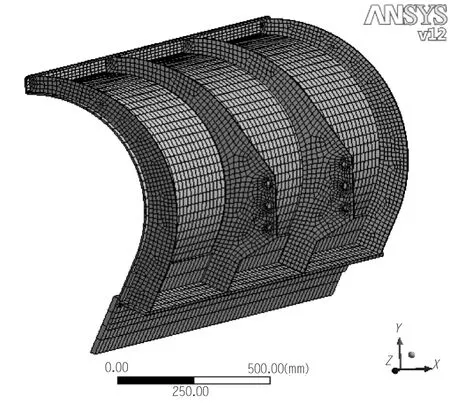
图2 除雪铲的有限元模型

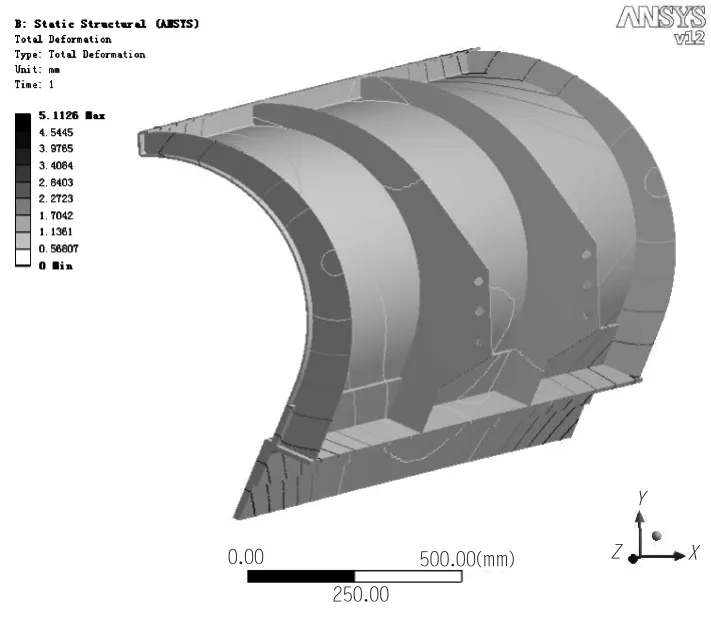
图3 除雪铲的变形分布图

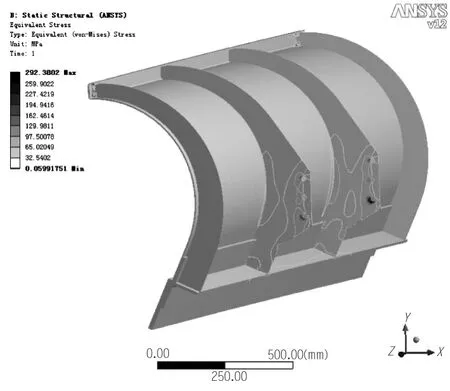
图4 除雪铲的应力分布图

正交试验是一种通过正交表合理安排试验，进而找出最优试验水平组合的试验设计方法，目前广泛地应用于多因素试验中［2，3］。在正交试验设计中，首先要明确试验目的，确定评价试验结果的指标。文章根据除雪铲强度分析的结果，将质量M、整体最大变形δ以及最大等效应力σ作为试验指标。在设计过程中，要求尽可能地减少除雪铲的质量M、最大变形δ以及最大等效应力σ，以得到较高结构强度的除雪铲。

2.2 正交试验设计

由于除雪铲结构复杂，设计尺寸较多，为了提高优化设计的效率，文章在考虑设计要求和制造工艺可行性的基础上，选择对上述优化目标影响较为显著的3个参数作为设计变量，即正交试验的3个试验因素，它们分别是除雪铲的铲板厚度H、筋板厚度t以及筋板个数N。结合各变量值的允许变化范围，安排如表1所示的4水平3因素的因素水平表。

根据表1的因素水平表，选择正交表L16（43）安排正交试验方案，并按照本文第一节的方法进行16次有限元数值仿真，仿真试验结果见表2。

表1 因素水平表

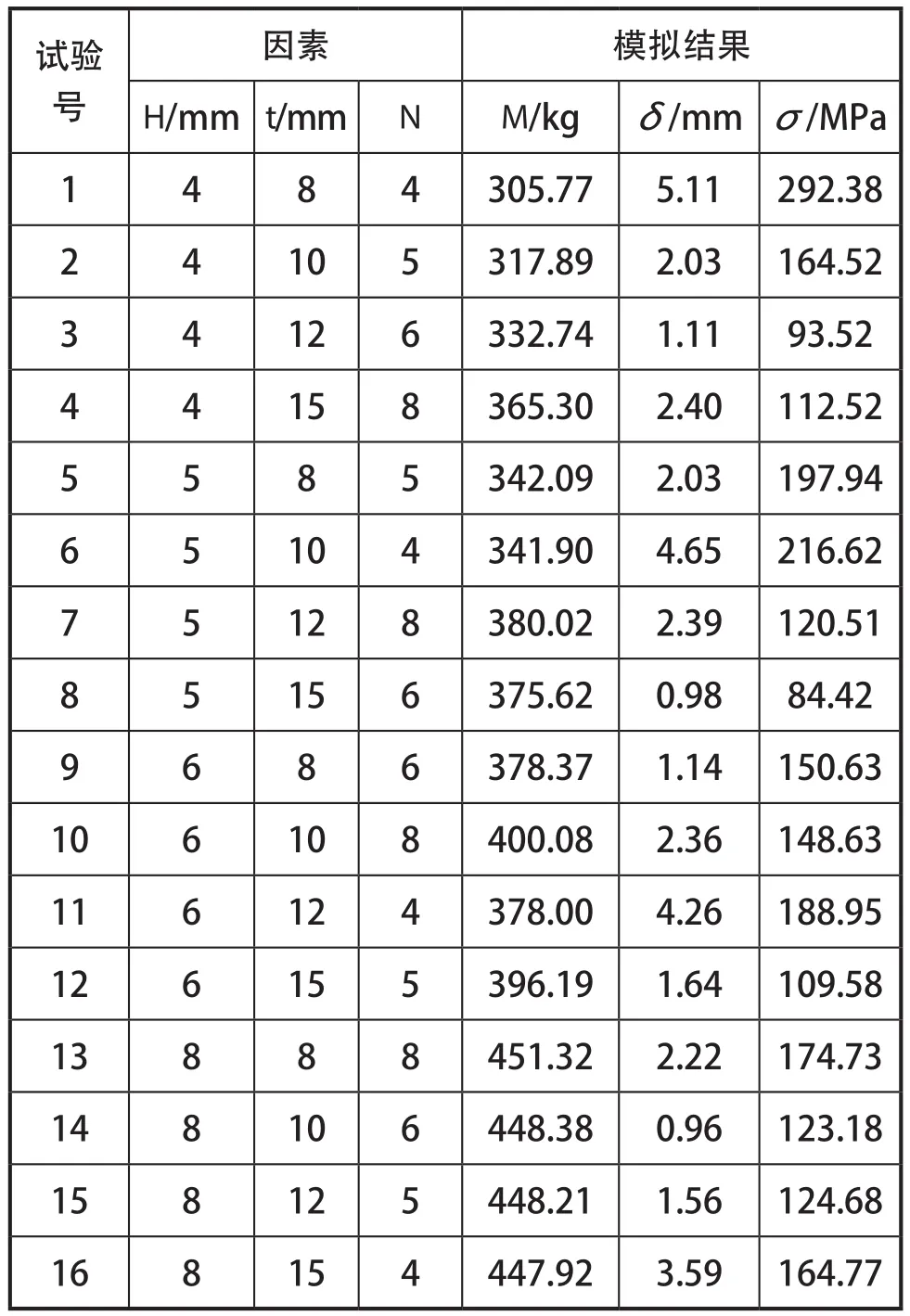
表2 仿真试验结果

3 灰色并联法的最优解

信息完全明确的系统称为白色系统，信息完全不明确的系统称为黑色系统，而信息部分明确、部分不明确的系统称为灰色系统。在灰色系统中，用关联度作为事物之间、因素之间的动态发展态势相似程度。关联度越大，事物之间的相似程度越大，否则关联度越小，也就是越不相似。

3.1 灰色分析的初始化

利用灰色系统理论进行多目标优化时，由于目标之间数据单位和范围不同，同时由于目标趋势不同，为保证各目标具有等效性和同序性，需要对原始数据进行处理，使之量纲一化［4，5，6］。

对于越大越好的评价指标，则处理为

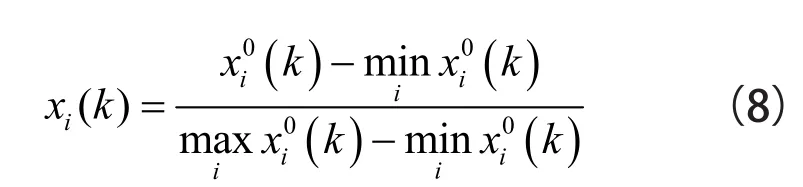
对于越小越好的评价指标（如除雪铲的质量、最大变形、最大应力），则处理为

式中i=1，2…，m；k=1，2…，n；m为试验次数，n为目标数目。xi0（k）为原始目标，xi（k）为处理后的目标；分别为xi0（k）的最大值和最小值。

3.2 目标函数的关联系数

设S（k）为xi0（k）的理想值，构造S（k）为

则经过数据变换后的xi（k）对于S（k）在第k点的灰色关联系数为

式中 ρ—— 分辨系数，ρ∈［0，1］，一般取0.5；Δ=|S（k）-xi（k）|。

按照式（9）、（10）、（11）对目标函数分别进行关联度计算，得到灰色关联系数，其对应的数值如表3所示。

3.3 目标函数的关联度

xi（k）对于S（k）在第i点的灰度关联系数的重要程度称为对于S（k）的关联度［7，8］，则关联度γi0为

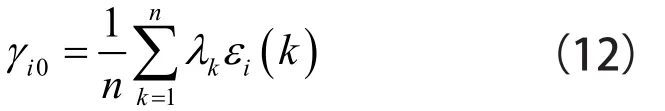
式中 λk—— 权重，本文中质量的权重系数

λM=0.4，最大变形的权重系数

λδ=0.3，最大应力的权重系数

λσ=0.3。

表3 目标函数的关联系数

根据式（8）-式（12），计算得到各仿真试验目标函数的关联度如表3所示。根据表3的结果分析可得除雪铲设计变量各水平的平均关联度，见表4。

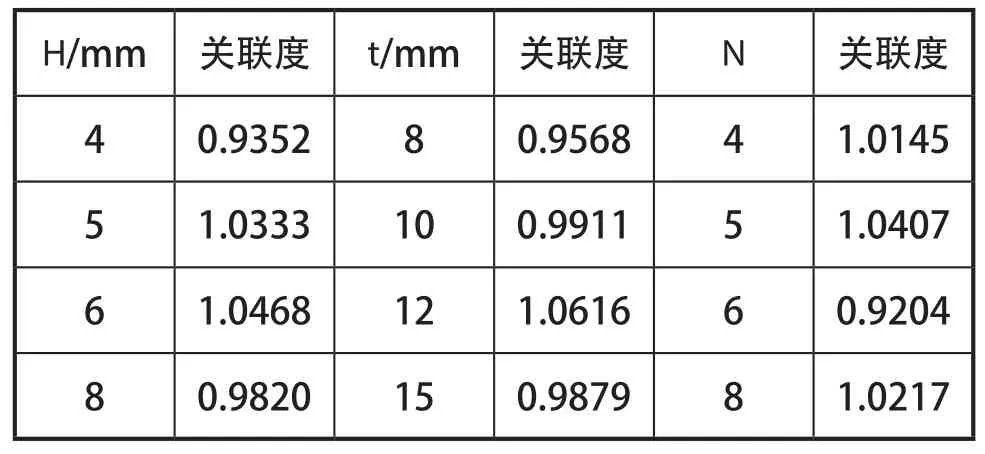
表4 设计变量对目标函数的平均关联度

3.4 灰色关联度的方差分析

对表4中每个影响因素的平均灰色关联度进行方差分析，可得到各个因素的各个水平对目标函数关联度的影响程度，见图5所示。

从图5可以看出，对灰色关联度影响最大的因素是筋板个数，其各水平间平均灰色关联度最大值和最小值相差为0.1203；其次是铲板厚度，其各水平间平均灰色关联度最大值和最小值相差为0.1115；而铲板厚度对灰色关联度影响最小，其各水平间平均灰色关联度最大值和最小值相差为0.1047。

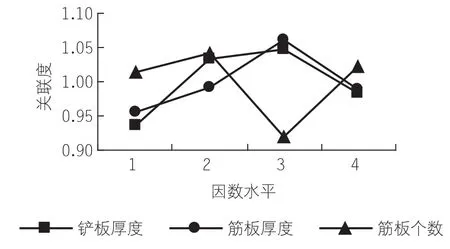
图5 各因素水平的关联度

对于一个因素来说，某水平的平均关联度值越大，表明该因素在此水平下的多目标响应越好，即该水平为相应因素的最佳水平。对于因素铲板厚度来说，最佳水平是水平3；对于因素筋板厚度来说，最佳水平是水平3；对于因素筋板个数来说，最佳水平是水平2。综上所述，除雪铲的最优设计尺寸为铲板厚度H=6mm，筋板厚度t=12mm，筋板个数N=5。