绝对平面检测方法的研究进展
2018-03-01黄元申吕昊宇
黄元申, 吕昊宇, 曾 媛,韩 森, 盛 斌
(1.上海理工大学 光电信息与计算机工程学院, 上海 200093;2.上海理工大学 上海市现代光学系统重点实验室, 上海 200093;3.上海理工大学 教育部光学仪器与系统工程研究中心, 上海 200093)
引 言
光学干涉法测量平面的精度很大程度上取决于参考平面的精度,为了进一步提高检测结果的精度和重复性,提出了绝对平面的检测方法,即通过对多次测量的结果进行计算,消除参考平面面形偏差的影响。这样的测量方式不仅提高了检测精度,对于高精度的光学平面加工意义重大,而且还降低了干涉测量系统中标准参考平面的加工精度要求。
1967年,Schulz等首次提出了三面互检方法,利用三个面形偏差较为接近的平面两两互检,由于测量过程中平面需要翻转,导致了测量位置变更,只能够得到翻转对称中心线上的绝对面形分布,精度可以达到λ/100[1]。随后,绝对平面检测的方法得到进一步研究和发展,从测量方式到计算方法都使测量精度得到了提高。
1 测量方式
1.1 平移剪切法
1983年,Keenan提出了伪剪切干涉法,通过平面平移方法先得到待测面绝对面形偏差,再积分得到待测面的绝对面形分布,但是仅限于理论上的结果[2]。2010年,Bloemhof通过实验验证了这种方法的测量精度优于λ/100[3],并于2014年利用差分方法证实在4 inch(1 inch=25.4 mm)口径中所测得的峰谷(PV)值可以达到λ/100[4]。
2015年,Huang等在差分方法的基础上提出共轭微分法,通过四次测量来获得平面的绝对面形分布[5],测量步骤如图1所示。
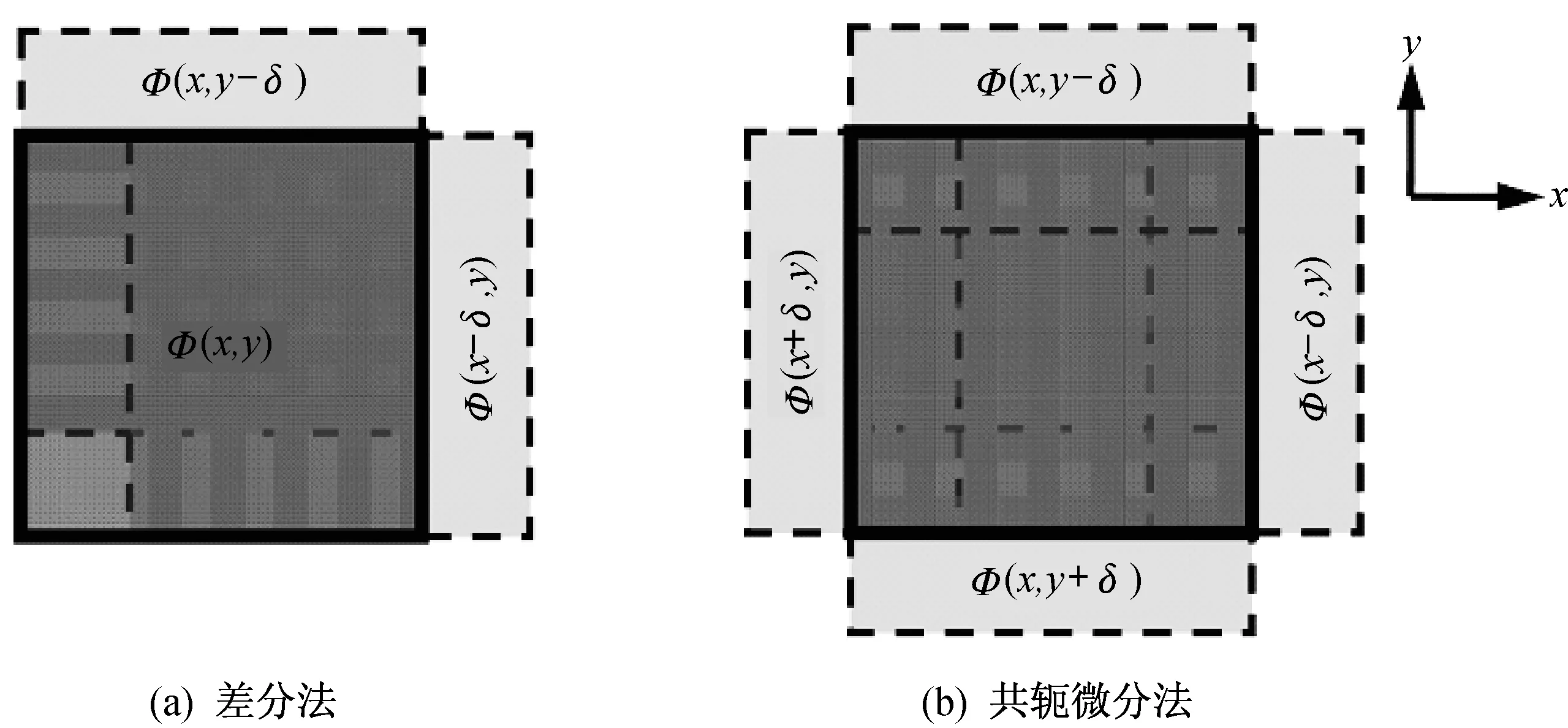
图1 差分法和共轭微分法测量步骤Fig.1 Experimental process of differential method and conjugate differential method

图2 多种方法实验结果对比Fig.2 Comparison of multiple methods of experimental results
最终通过实验证实,采用共轭微分方法的绝对平面测试,提高差分数据的精度和减少测试步骤之间的耦合,可提高测试结果的可靠性。共轭微分法的绝对面形分布结果与实验中的三平面测试的结果吻合良好,PV值达到了4.2 nm,图2为多种计算结果的对比。
1.2 旋转剪切法
2001年,Freischlad提出了旋转剪切法,该法是在传统三面互检法的基础上任选一组并对其中一个面进行5次旋转剪切,同时用傅里叶变换的方法对剪切波面进行处理,复原出三个平面的绝对面形分布,测得150 mm口径的平面PV值为22.7 nm[6]。2015年,Liu等分析了旋转角误差的影响,角度误差控制在1°,并通过对比验证了全孔径绝对测量结果的PV值达到0.026 6λ[7]。
1.3 旋转平移法
1990年,Grzanna等提出了一种新的三平面互检法,除了三个平面两两互检外,该方法还将一个面进行90°旋转和平移[8]。2012年,Fujimoto等提出了两平面绝对测量的旋转平移法[9],同年,Su等提出了一种基于Zernike多项式的旋转平移绝对检测法[10]。2013年,Song等也通过将旋转平移的方法与传统的三平面互检的方法对比,验证了标准平面镜的PV值为5.29 nm[11]。
随着数控系统的发展以及步进电机的广泛应用,像素级精度的位移和旋转以及整个测量过程的自动化被大量应用在绝对平面检测中,使检测结果有效地避免了如装调、环境等因素带来的影响。
2 计算方法
2.1 Zernike方法
1983年,Fritz利用Zernike多项式,对波面面形的耦合系数通过增加一次绕光轴旋转的测量,得到了三个平面的绝对面形分布,并验证了8 inch孔径的光学平面PV值为λ/100,但由于其计算方法的限制,若旋转的角度为360°/N(N为Zernike多项式对应倍角,N=2,3,4,…),则无法通过Zernike系数计算出三个平面的绝对面形分布,而且计算的结果是Zernike多项式的拟合结果,与真实值之间还有偏差[12]。2013年,Han等提出了基于三面互检法的斜入射法,通过Fizeau干涉仪的一次干涉测量和两次斜入射测量,用Zernike方法得到整个待测面的绝对面形分布,在90 mm口径的平面上测得0.059λ的PV值和0.014λ的均方根值(RMS)[13]。
2.2 奇偶函数法
1992年至1993年,Ai等将平面面形在笛卡尔坐标系分别关于x轴和y轴的奇偶函数分解成偶-偶、奇-偶、偶-奇、奇-奇四部分,通过六次测量并计算得到三个平面的绝对面形分布,得到λ/30的PV值。但是奇-奇部分无法完全获得,便由倍角关系拆分,再通过三次旋转依次求出前三项,而省略了高倍角项[14- 15]。2000年,Han等提出在Firtz四次测量的基础上通过奇偶法计算得出绝对面形分布[16]。2017年,Li等使用四次测量奇偶法得到λ/50的PV值[17]。
2.3 迭代算法
2007年,Vannoni等提出了三平面互检的迭代算法,能精确计算并合成干涉图,结果和Zernike法相一致,PV值达到7.31 nm,该方法简单、快速、且可用到球面测试中[18],2008年,他们将这种迭代计算的方法直接应用到Zernike方法的计算结果上,得到4.9 nm的PV值[19]。2011年,Morin等又针对不同的旋转角度和迭代因子进行了对比和验证[20]。2014年,Vannoni利用斜入射装置进行干涉测量[21],偏差的PV值可以计算到3 nm。
Gao等则是在四次测量迭代算法的基础上,在每一个差值计算后都重新生成一次平面面形并带入到下一个差值的计算中,大大加快了新结果的产生速度,很大程度提升了迭代算法的计算效率[22],如图3所示。
He等提出奇偶迭代算法,首先计算关于y轴为偶函数的部分,然后再通过迭代算法去计算奇函数的部分,也可以提升迭代算法的计算效率[23],如图4所示。
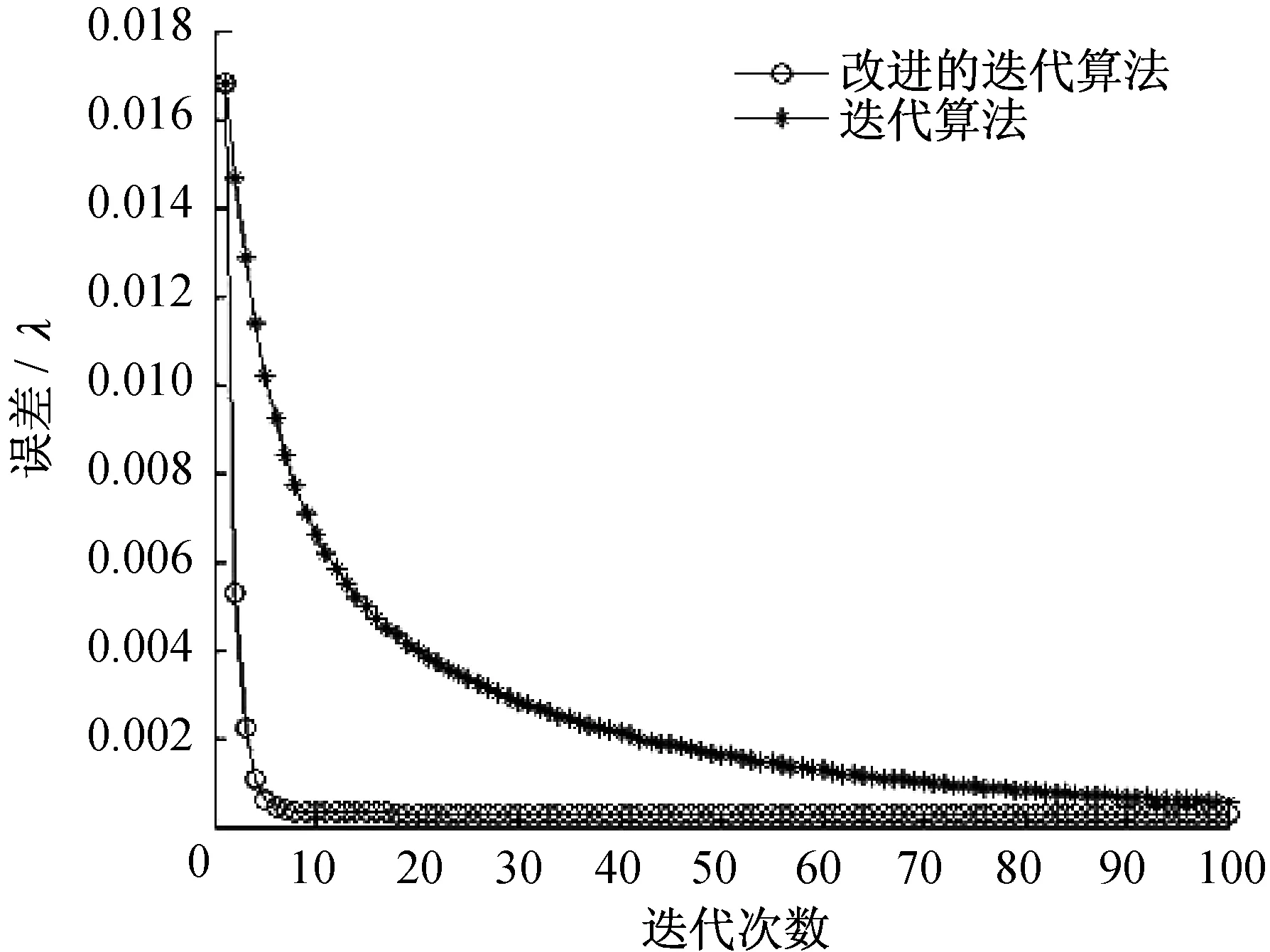
图3 迭代算法的改进对迭代计算效率的影响Fig.3 Influence of the improved iterative algorithm over the iterative computational efficiency

图4 奇偶迭代算法的效率提升Fig.4 Efficiency improvement of the parity iterative algorithm
2016年,He等通过对旋转平移法的迭代计算进行仿真实验,验证了其方法对非旋转对称和旋转对称两部分绝对面形分布迭代计算的可行性[24],面形偏差PV值达到了2.47 nm。
迭代算法可以将计算结果与原始数据的偏差作为一个因子返回给面形结果,通过大量的迭代计算可以快速逼近理想结果。但是这种计算方法需要设置合适的反馈因子以及原始面形,同时这种计算结果不易进行误差分析。
2.4 矩阵分析
2014年,Song等将旋转和平移的结果建立矩阵,在像素级空间分辨率基础上求解出了两个平面的绝对面形分布,得到1.67 nm的PV值,着重消除了中高频偏差[25]。
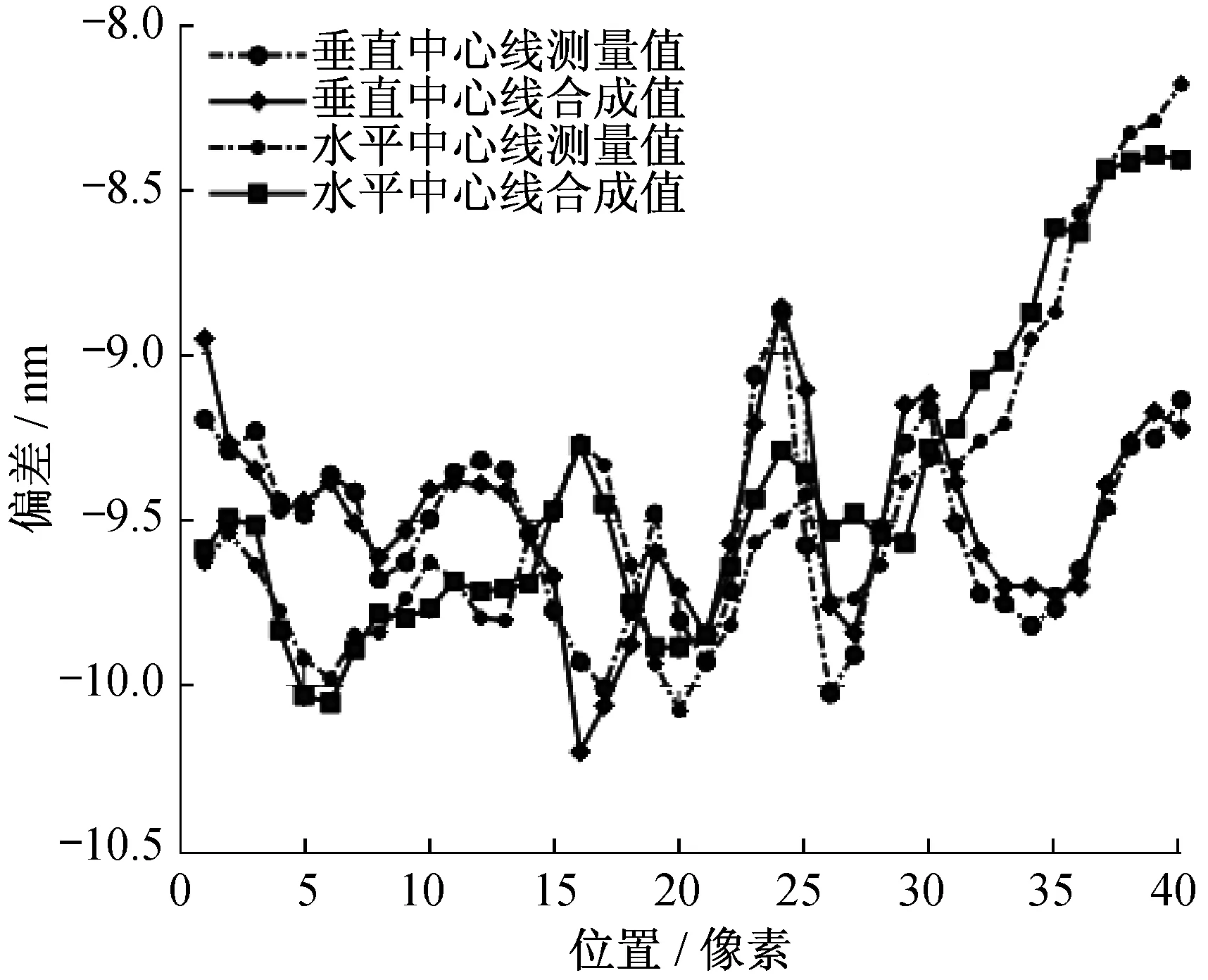
图5 被测平面测量和计算求解的结果对比Fig.5 Comparison of the results of two planar measurements and calculations
通过矩阵代入每一个像素点的位置,就可以得到整个表面的信息。由图5可以看到,分离后的表面信息与测量结果基本吻合。 2016年,Han等在斜入射装置的测量结果中引入了极坐标系下的矩阵分析[26],将测量的波前图转换为极坐标数据,通过矩阵分析得到极坐标反射平面的轮廓,再将反射平面的轮廓变换成笛卡尔坐标数据。测得标准平面的PV值结果为0.07 nm,图6对比了极坐标矩阵、Zernike拟合以及迭代方法的计算误差。
矩阵分析的方法是通过一组闭合数学形式,而避免了多项式波前拟合以及迭代计算,可以更有效地进行绝对测试。但是矩阵分析一般是针对于像素点,由于矩阵计算的限制,并不适用于所有绝对检测方法。

图6 不同方法的计算误差Fig.6 Calculation errors of different methods
3 结 论
随着计算机的发展和普及,数字化信息的处理已经精确到像素级别,大量的数据分析和处理方式被应用到绝对平面检测中去。平移剪切法、旋转平移法由于位移和旋转平台精度的提高逐渐开始被应用;迭代算法、矩阵分析得益于计算机的发展,大量的计算工作也可以快速有效地进行。对于不同的使用环境和工作范围,这些方法也各有所长:平移剪切法和旋转平移法理论上可以仅用两个平面就能获得绝对检测结果,在坐标转换过程中存在大量的近似计算;迭代法便于通过计算机直接计算得到,但不利于对迭代的结果进行误差分析;矩阵分析的方法可以直接使用原始数据进行计算,但由于矩阵本身计算的限制,不能应用到所有的检测计算方法中。虽然还存在着这些问题,但这些方法都已经在计算的速度、精度以及重复性上取得了显著的提高。
[1] SCHULZ G,SCHWIDER J.Precise measurement of planeness[J].Applied Optics,1967,6(6):1077-1084.
[2] KEENAN P B.Pseudo- shear interferometry[C]∥Proceedings volume 0429,precision surface metrology.San Diego,United States:SPIE,1983:2-7.
[3] BLOEMHOF E E.Absolute surface metrology by differencing spatially shifted maps from a phase- shifting interferometer[J].Optics Letters,2010,35(14):2346-2348.
[4] BLOEMHOF E E.Absolute surface metrology with a phase- shifting interferometer for incommensurate transverse spatial shifts[J].Applied Optics,2014,53(5):792-797.
[5] HUANG Y,MA J,ZHU R H,et al.Absolute measurement of optical flat surface shape based on the conjugate differential method[J].Optics Express,2015,23(23):29687-29697.
[6] FREISCHLAD K R.Absolute interferometric testing based on reconstruction of rotational shear[J].Applied Optics,2001,40(10):1637-1648.
[7] LIU H H,LIU S J,GAO W R,et al.Research of absolute testing based on N- position rotations[C]∥Proceedings volume 9796,selected papers of the photoelectronic technology committee conferences.Various,China:SPIE,2015:97960P.
[8] GRZANNA J,SCHULZ G.Absolute testing of flatness standards at square- grid points[J].Optics Communications,1990,77(2/3):107-112.
[9] FUJIMOTO I,TAKATSUJI T,NISHIMURA K,et al.Autonomous calibration method of the reference flat surface of an interferometer without using a standard flat surface[J].Applied Optics,2012,51(20):4754-4767.
[10] SU D Q,MIAO E L,SUI Y X,et al.Absolute surface figure testing by shift- rotation method using Zernike polynomials[J].Optics Letters,2012,37(15):3198-3200.
[11] SONG W H,WU F,HOU X,et al.Absolute measurement of flats with the method of shift- rotation[J].Optical Review,2013,20(5):374-377.
[12] FRITZ B S.Absolute calibration of an optical flat[C]∥Proceedings volume 0433,contemporary methods of optical manufacturing and testing.San Diego,United States:SPIE,1983.
[13] HAN Z G,CHEN L,WULAN T,et al.The absolute flatness measurements of two aluminum coated mirrors based on the skip flat test[J].Optik- International Journal for Light and Electron Optics,2013,124(19):3781-3785.
[14] AI C,WYANT J C.Absolute testing of flats decomposed to even and odd functions[C]∥Proceedings volume 1776,interferometry:surface characterization and testing.San Diego,CA,United States:SPIE,1992.
[15] AI C,WYANT J C.Testing an optical window of a small wedge angle:effect of multiple reflections[J].Applied Optics,1993,32(25):4904-4912.
[16] HAN S,NOVAK E.High- accuracy absolute flatness testing using a commercial interferometer[C]∥Proceedings volume 4231,advanced optical manufacturing and testing technology 2000.Chengdu,China:SPIE,2000.
[17] LI Y C,LI X Y,WANG Q Z,et al.Measurement of high accuracy flatness using a commercial interferometer[C]∥Proceedings volume 10255,selected papers of the chinese society for optical engineering conferences.Jinhua,Suzhou,Chengdu,Xi’an,Wuxi,China:SPIE,2017:102551H.
[18] VANNONI M,MOLESINI G.Iterative algorithm for three flat test[J].Optics Express,2007,15(11):6809-6816.
[19] VANNONI M,MOLESINI G.Absolute planarity with three- flat test:an iterative approach with Zernike polynomials[J].Optics Express,2008,16(1):340-354.
[20] MORIN C,BOUILLET S.Absolute calibration of three reference flats based on an iterative algorithm:study and implementation[C]∥Proceedings volume 8169,optical fabrication,testing,and metrology IV.Marseille,France:SPIE,2011:816915.
[21] VANNONI M.Absolute flatness measurement using oblique incidence setup and an iterative algorithm.A demonstration on synthetic data[J].Optics Express,2014,22(3):3538-3546.
[22] GAO B,LI Q,HE Y H,et al.Improved iterative algorithm for the three- flat test[J].Optical Engineering,2014,53(9):092004.
[23] HE Y H,GAO B,XU K Y,et al.Iterative algorithm for absolute planarity calibration in three- flat test[J].Optics Express,2014,22(22):27669-27674.
[24] HE Y H,LI Q,WAN D M,et al.New reconstruction algorithm for absolute shape calibration in two- flat test[C]∥Proceedings volume 9684,8th international symposium on advanced optical manufacturing and testing technologies:optical test,measurement technology,and equipment.Suzhou,China:SPIE,2016:96842N.
[25] SONG W H,HOU X,WU F,et al.Absolute interferometric shift- rotation method with pixel- level spatial frequency resolution[J].Optics and Lasers in Engineering,2014,54:68-72.
[26] HAN Z G,YIN L,CHEN L,et al.Absolute flatness testing of skip- flat interferometry by matrix analysis in polar coordinates[J].Applied Optics,2016,55(9):2387-2392.
