基于积分实验对232Th共振参数的调整

赵秋娟 吴海成 吴小飞 张环宇

摘要

为验证钍基熔盐堆用AMPX格式238群中子-48群光子耦合多群常数库在钍铀装置核临界安全分析中的适用性，选取了钍铀物理基准实验（ICSBEP标识为HEU-COMP-THERM-021）的100个临界装置对该库进行基准检验。计算结果与实验值出现了从10pem到1600pcm不等的偏差。选取合适的积分实验，并利用中国核数据中心研制的核数据调整程序NDAC对²³²Th共振参数进行了调整，重新计算临界基准实验得到的计算值与实验值的偏差只比调整前降低了60到90pcm。虽然调整后偏差降低了，但降低的幅度与预期结果相差较大。可能的原因有两个：一是灵敏度矩阵计算方法或精度不够可靠;二是该问题不满足核数据调整原理中的线性假设。下一步需要研究更好更精确的灵敏度矩阵计算方法并尝试通过迭代方法解决非线性问题。

【关键词】核数据调整 灵敏度 临界基准检验

1 引言

核数据是重要的基础数据，在核科学和核技术中有着广泛的应用。模拟计算的准确度取决于三个方面：物理模型、计算程序和核数据。随着计算技术及输运理论的不断发展，前两个因素的影响基本可以忽略，而核数据本身的不确定度就成为影响计算结果准确度的主要因素。核数据的制作过程引入了诸多不确定度，需要通过宏观检验来验证其可靠性。目前，国际上已经在大量基准实验的基础上进行了大量宏观检验比对工作，建立了趋势分析、灵敏度分析等方法，但是对检验结果的分析仍不足。因此，发展量化分析技术、实现宏观检验对评价数据的直接改进反馈，是今后宏观检验的发展方向。

国际上早在70年代就提出了宏观检验直接改进核数据的解决方法：基于广义最小二乘法，利用积分实验与协方差数据相结合对核数据进行调整。NEA/WPEC组织SG33对该方法进行了回顾总结，指出采用积分实验和协方差数据组合应用对核数据进行定量调整确实是改进核数据，进而降低核装置积分参数的不确定度的有效方法。因此，中国核数据中心以最大似然函数法为基础，研发了核数据调整程序NDAC。只要针对特定堆型，选择合适的积分实验，程序就可以根据用户提供的核数据及其协方差数据、积分实验数据以及灵敏度数据对输入核数据进行调整，得出积分量的最佳估计值以及降低它的不确定度，并输出调整后的结果，包括核数据、协方差、积分量及其不确定度。

另一方面，为满足新一代核能系统钍基熔盐堆核临界安全分析用多群常数库的需求，研制了一套AMPX格式的238群中子一48群光子耦合多群常数库，命名为CENDL-TMSR-AMPX。为了验证该库在钍铀装置核临界安全分析中的适用性，选取了钍铀物理基准实验（ICSBEP标识为HEU-COMP-THERM-021，简写为HCT021）的100个临界装置对该库进行基准检验。在2012年核数据宏观参数研究与应用会议中吴海成研究员的报告《最新评价核数据库的临界基准检验——ENDITS-1.0开发与应用》中指出对于HCT021系列热装置中case14～53的40个装置，各家计算结果均整体高估，并出现随能谱变硬keff的C/E值偏大的能谱偏倚，再次显示²³²Th（n，γ）共振截面仍需改进。因此希望利用核数据调整程序，通过宏观检验对评价数据进行直接的改进反馈，这也是今后宏观检验的发展方向。

2 核数据调整方法的基本原理

核数据调整方法的基本原理是基于广义最小二乘法，利用小的积分实验不确定度来改进核数据以及模拟积分参数。中国核数据中心研发的核数据调整程序NDAC是以最大似然函数法为理论基础的。下面给出调整后核数据、积分量、核数据协方差、积分量的不确定度及卡方最小值的表达式。

表1中给出公式中变量名的定义。

公式推导过程中假设调整后的积分量可以线性预测：

其中，H为I_c的灵敏度。

则调整后的核数据应满足：

积分量的最佳估计为：

调整后的核数据协方差为：

（4）

调整前I_c的不确定度为：

调整后积分量的不确定度为：

卡方最小值：

3 积分实验及所要调整核数据的选定

3.1 积分实验的选定

HCT021的case14～53这40个装置是通过燃料棒个数、水的临界高度以及水中硼浓度的变化来实现能谱指标EALF的值从0.196eV到0.291eV缓慢变化的。因此这40个装置的相似度非常高，所以在对核数据做调整时不必对这40个装置都进行计算，只需从中挑选出几个装置，这几个装置要能够反映出随着能谱变硬k_eff的C/E值偏大的能谱偏倚，最后再用其余装置作校验即可。积分实验的选取结果如表2及图1中黄色圆点所示。图1中的CENDL-TMSR-ACE是中国核数据中心基于CENDL-TMSR微观评价核数据库研制的蒙特卡洛程序用ACE格式库。

3.2 所要调整核数据的选定

对于HCT021系列实验而言，慢化剂中的¹H，增殖材料²³²Th和燃料中的²³⁵U是对临界计算结果影响最大的三种核素。利用SCALE5.1程序系统中的TStJNAMI-3D可以计算得到基准装置积分量k_eff对这三种核素核反应截面的灵敏度随能量的变化关系。分析发现，正反应性贡献依次主要来源于¹H（n，el）、²³⁵U（n，f）和²³²Th（n，sct）反應，负反应性贡献依次主要来源于²³²Th（n，γ），²³⁵U（n，γ）和¹H（n，γ）反应。考虑到，¹H、²³⁵U在与HCT021能谱软硬程度相近的LCT006（ICSBEP标识为LEU-COMP-THERM-006）系列装置中，k_eff计算值与实验值符合良好。可以断定，²³²Th的评价数据是导致HCT021系列装置k_eff高估的主要原因。对比²³²Th（n，γ）和（n，sct）反应在HCT021系列装置中贡献的大小，可知²³²Th（n，γ）截面的高估是该系列实验k_eff高估的主要原因。从²³²Th（n，γ）截面灵敏度随能群的分布可知，²³²Th（n，γ）截面对k_eff的负反应性贡献主要来源于IeV以下的宽共振和1/v截面区。因此要调整的核数据为²³²Th共振参数，包括前十个共振能量对应的中子宽度和辐射俘获宽度，见表3。其中前八个共振能量为负，负共振对共振俘获的贡献很大，后两个共振能量对应的共振参数的调整是为了调整前两个共振峰。

4 输入数据的准备

根据调整后核数据、积分量等物理量的计算公式，可以看出要计算这些量，需要给出的数据包括调整前的核数据、调整前核数据的协方差、调整前积分量的实验值和计算值、积分量的协方差以及灵敏度。其中调整前的核数据见表3;调整前积分量的实验值在国际核临界安全手册ICSBEP中查得;调整前积分量的计算值的计算方法是首先将ENDF格式的核数据加工成MCNP程序用的ACE格式数据文件，再用MCNP程序计算得到五个临界基准装置的k_eff;积分量的协方差则假设不同临界基准实验之间互不关联，相同实验关联系数为1。下面只对调整前核数据协方差和灵敏度的计算作简单介绍。

4.1 调整前核数据的协方差

设协方差矩阵V=（V_ij）_n×n，则有

其中，D为不确定度，C=（C_ij）_n×n为关联系数矩阵。C_ij的对角元素（也就是i=j的元素）的值通常为1.0，因此不在评价数据文档中给出。协方差的给出需要分别给出不确定度及关联系数矩阵，而协方差的计算在NDAC程序中完成。并注意这里需要给出Γ_n和Γ_n、Γ_n和Γ_γ、Γ_γ和Γ_γ的关联系数矩阵。调整前²³²Th共振参数的不确定度和关联系数矩阵要从²³²Th评价数据文件的MF-32，MT=151中提取相关信息并计算得到。

4.2 核数据的灵敏度

灵敏度矩阵的个数与积分实验装置的个数相同，为五个。根据灵敏度的定义，让每一个共振能量对应的共振宽度Γ_n和Γ_γ变化±1%，即Γ⁺和Γ^-，求出基准实验装置积分量的值k⁺和k^-;原来共振宽度对应的积分量计算结果为k;利用差分方法计算出相对灵敏度：

计算相对灵敏度的基本思路是将共振宽度调整后的评价数据文件用NJOY99程序系统加工成ACE格式文件，用MCNP程序对临界基准装置进行建模并计算得到积分量k_eff的值。对评价数据文件中的20个共振宽度分别变化±1%，计算五个临界基准装置的k_eff，利用（9）式计算出相对灵敏度。选择用ACE数据文件配套MCNP程序来计算积分量k_eff的值是因为ACE数据文件即连续点截面格式，数据的加工和建模中的近似都较小，而多群常数库的制作过程中的物理过程较多，如共振处理方法的不同，会带来更多的不确定性。得到的五个装置的灵敏度矩阵见表4。

5 计算结果与分析

5.1 计算结果

调整后²³²Th的共振参数如表5所示。

NDAC程序给出的调整后的积分量k_eff的C/E值如表6中第3列数据所示。将NDAC程序得到的调整后的共振参数的值放入²³²Th评价数据文件中MF=2，MT=151的对应位置上，再重新加工ACE格式数据文档，用MCNP程序计算选定的五个积分实验装置的k_eff，得到的计算结果如表6中第4列数据所示。

5.2 结果分析

利用NDAC程序给出的调整后的232n共振参数，重新计算临界基准实验得到的计算值与实验值的偏差都降低了，但只比调整前降低了60到90pcm，降低的幅度与NDAC程序给出的调整后k，的c爪值相差较大，可能的原因有两个：

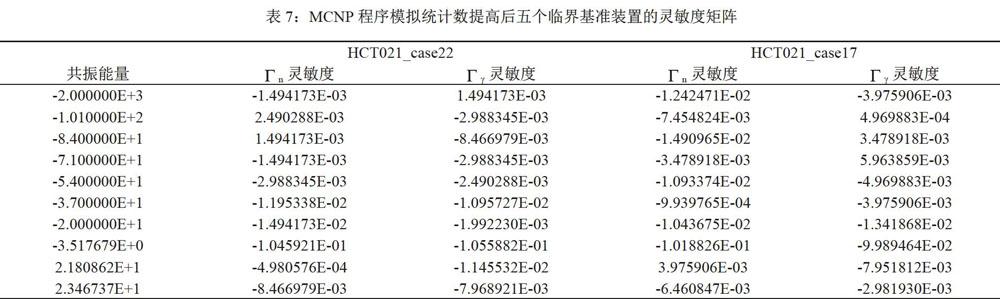
一是灵敏度矩陣计算方法或精度不够可靠。之所以说灵敏度矩阵计算精度不够，是因为用MCNP程序计算得到的k_eff的标准差的第一位有效数字在万分位上，那么k_eff的值从万分位上甚至千分位上开始就是不准确的，则计算得到的灵敏度矩阵可能会存在精度不够的问题。为了得到更高的精度，将MCNP模拟的统计数从10⁷提高到10⁸，计算得到的灵敏度矩阵见表7。按照上述步骤重新计算五个临界基准装置得到的k_eff的计算结果见表8，可以看出MCNP模拟统计数提高后仍然没有解决根本的矛盾。若是灵敏度矩阵计算方法不够可靠，则需要找到更好更精确的计算方法，有待进一步研究。

二是该问题不满足核数据调整原理中的线性假设，即公式（1）不满足。目前看来，更可能的原因是该问题存在很严重的非线性问题，在计算灵敏度矩阵中的k+和k-时可以看出。设Γn（N）-和Γn（N）+分别代表第N个中子宽度下调1%和上调1%，Γ_γ（N）-和Γ_γ（N）+分别代表第N个辐射俘获宽度下调1%和上调1%，N为1～10。对于同一个共振宽度Γ_n（N）或Γ_γ（N），将它下调和上调1%得到的k_eff都变小或都变大，则说明存在非线性问题。线性情况下，对于同一共振宽度，将它下调和上调1%得到的k_eff的变化方向应该相反。下一步将建立迭代手段，尝试通过迭代的方法解决非线性问题。

6 结束语

为了验证中国核数据中心研制的AMPX格式238n-48γ多群常数库在钍铀装置核临界安全分析中的适用性，选取了钍铀物理基准实验（ICSBEP标识为HEU-COMP-THERM-021）的100个临界装置对该库进行基准检验。计算结果与实验值的偏差较大。选取合适的积分实验，利用NDAC程序对²³²Th共振参数进行调整，并制作调整后的ACE数据文档，用MCNP程序重新计算临界基准实验得到的积分量计算值与实验值的偏差都降低了，但降低的幅度与预期相差较大，可能是灵敏度矩阵计算方法或精度不够可靠;也可能是非线性问题，下一步需要找到更好更精确的灵敏度矩阵计算方法或尝试通过迭代的方法解决非线性问题。

參考文献

[1]WPEC/SG26.Uncertainty and TargetAccuracyAssessment for InnovativeSystems using Recent Covariance DataEvaluations.OECD/NEA，NEA/NSC/WPEC/DOC（2008）445，2008.

[2]WPEC/SG33.Methods and Issues for theCombined Use of Integral Experimentsand Covariance Data.OECD/NEA，NEA/NSC/WPEC/DOC（2013）445，2013.

[3]WPEC/SG33.Assessment of ExistingNuclear Data AdjustmentMethodologies.OECD/NEA，NEA/NSC/WPEC/DOC（2010）429，2010.

[4]覃英参.核数据调整程序NDAC的研制及初步应用[D].硕士论文，2010.

[5]International Handbook of EvaluatedCriticality Safety BenchmarkExperiments[R].Organizationfor Economic Co-operation andDevelopment，NuclearEnergy Agency（OECD-NEA），NEA/NSC/DOC（95）03/I-VII，September 2006 Edition.

[6]吴海成，等.最新评价核数据库的临界基准检验——ENDITS-1.0开发与应用[R].内部资料.2012.

[7]Poenits，W.P.，The SimultaneousEvaluation of Interrelated Cross-sections by Generalized Least-squaresand Related Data File Requirements，Proc.Adv.Grp.Meet.on Nuclear StandardReference Data，Geel，Belgium，November1984，International Atomic AgencyReport IAEA-TECDOC-335（1985）.

[8]Poenits，W.P.，GMADJ-A Code forGeneralized Least-squares Adjustmentsto Derived Quantities with AdditionalExperimental Data，forthcoming.

[9]Saint Jean，C.de，etal.，Proceedingsof the International Conferenceon Nuclear Data for Science andTechnology，Nice，France，2007，0.Bersillon，et al.（E d.），EDPScience（2008）.

[10]Faleschini，B.，M.Petilli，MARA：AGeneralized Least Squares Methodfor Nuclear Data Adjustment，to bepublished.

[11]G.N.Manturov.Codes and ArchivesINDECS System.-VANT.Series：Nuclear Constants.Issue 5（89），MOScow，1984，p.20-24（in Russian）.

[12]G.N.Manturov.Influence of NeutronData Uncertainties on Accuracy ofPrediction of Advanced ReactorCharacteristics.-Proc.of Intern.Conf.on Nuclear Data for Scienceand Technology，May 9-13 1994，Gatlinburg，Tennessee.Vol.2，p.993-999（1994），ORNL，ANS.

[13]吴海成.钍基熔岩堆设计用中子评价数据库（CENDL-TMSR）推荐[R].内部资料，2012.

[14]A.Trkov，M.Herman，D.A.Brown.ENDF-6 Formats Manual[R].Nat iona INuclear Data Center，BrookhavenNational Laboratory，2013.

[15]R.E.MacFarlane，D.w.Muir.NJOY99.0，Code system for producingpointwise and multigroup neutronand photon cross sections from ENDF/B Data[R].USA：Los AlaMOS NationalLaboratory，2000.

[16]X-Monte-Carlo Team.MCNP-A GeneralMonte Carlo N-Particle TransportCode，Version 5[R].Los AlaMOSNational Laboratory，2003.