基于Kriging数据内插的非直达波定位方法

吴保德

摘要

在蜂窝移动定位系统中，定位精度的好坏主要由非直达波传播问题引起，采用非参数核方法可以在一定程度上抑制非直达波传播对定位性能的不利影响，然而该方法对样本信息没有充分使用，故可以进一步改善。本文提出一种基于Kriging数据内插的改进非参数核方法，该方法能有效利用样本信息，在不同样本个数环境下，能有效抑制非直达波误差，提高定位精度。仿真实验显示本文所提出的方法性能接近CR1B下限。

【关键词】移动定位 非直达波误差 核方法Kriging内插

1 引言

解决非直达波传播所带来的问题，在蜂窝移动定位系统中，对定位精度的改善有极大的意义。目前抑制非直达波误差的思路主要有两种，一是参数化方法，如利用散射体信道模型、消极加权等，然而环境决定非直达波的误差，故参数化方法在抑制非直达波误差过程中，不具有广泛性;二是非参数方法，该类方法利用外场实测数据或经验模型得到样本信息，利用样本信息描述无线信道环境，从而抑制非直达波误差。对于非参数核方法，该方法对非直达波传播造成的问题有一定作用，然而该方法未能有效利用样本信息，故可以进一步改善，本文拟用数据插值的方式增加样本点的数目，提出基于Kriging数据内插的改进非参数核方法，使得算法能有效利用样本信息，适用于不同的样本条件。

2 利用Kriging方法对现有数据进行插值

本文考虑TOA（time of arrival）定位方法，同时本文算法可直接扩展到TDOA（timedifference of arrival）、SOA（strength of arrival）等定位方法。设（x_i，y_i）为第i个基站坐标，i=1，…N，N为站点数目，估计域内共有M个已知样本点，其位置为（sx_j，sy_j），Z_j∈A，j=1，…，M为已知样本点的测量矢量，A=[Z₁…Z_M]为已知样本点测量矢量的集合，Zj=[z_j1，…，z_jN]^T，其中z_ji为第i个已知样本点相对于第i个基站的距离测量值：

其中n_ji为零均值，标准差为σ的高斯分布，e_ji为非直达波传播造成的正性误差。Kriging算法利用加权平均的方法来得出待估值。即：

其中z_0i为待估点（sx₀，sy₀）处的对第i个基站距离测量值的估计值，λ_j为权值系数。Kriging方法的目的是在限制条件估计量无偏和估计方差最小情况下，获得M个权值系数。要使z_0i为待估计点（sx₀，sy₀）处真值z_0i的无偏估计，即要求由此可得：

进一步推导，可得到估计方差表达式，在无偏性的前提下，要让估计方差最小，可以利用拉格朗日乘子法，即令：

对λ_j和μ求偏导，并使其为零，可得Kriging方程组：

写成矩阵形式：

Kλ=D（7）

解式（7），可得权值系数：

从而可求得待估点（sx₀，sy₀）处的估计值，通过利用实验变异函数（9），求解变异函数γ，进而求解式（7）：

其中h为点（sx_j，sy_j）到点（sx_k，sy_k）的距离，N（h）为样本中间距小于h的样本点组数。通过对实验变差函数进行拟合，来达到对未知值估计，本文利用指数模型对其拟合，因为在仿真中看出具有线性特性时，实验变差函数是在零点处，故：

因此利用已知样本点样本值Z_j通过式（9）可得实验变异函数，再使用式（10）模型进行拟合，最后代入式（8）可解得权值系数λ，最后结合λ和式（2），可以得到待估点（sx₀，sy₀）处的估计值z_0i。

3 利用非参数核方法对移动站进行定位

本文以优于文献[3]的方法，先用Kriging方法对已知样本点集合进行插值扩展，再通过非参数核方法进一步定位移动站，提高非参数核方法的定位精度。由第二部分的Kriging方法可得到扩展后的样本点测量集合：

其中A_N×M为事先测量的样本点矢量集合，A_N×U'为插值得到的估计矢量集合，U为插值点的个数，。这里采用最小均方误差（MMSE）准则，估计移动站位置：

其中θ=[xy]^T为移动站位置，f（θ|Z）为θ在θ处测量矢量Z下的条件概率密度函数，S为移动站可能位于的区域，该信息可由服務基站提供。采用贝叶斯公式，可将式（12）转换为：

其中f（θ|Z）为θ和Z的联合概率密度函数，这里采用不受限于环境因素的方法，即非参数核方法，利用已知数据直接估计概率密度函数。其中联合概率密度函数f（θ|Z）可写为多个核函数的线性组合：

其中K_z和K_θ为核函数，h_z，h_θ为平滑常数。

在文献[3]中Parzen Laplace核函数具有良好的性能，这里也采用该函数对联合概率密度进行拟合：

其中‖x‖¹为x到原点的L₁距离，由式（13）（14）可算出移动站的位置：

其中θ_j=[sx_jsy_j]^T，为与样本点测量矢量Z_j相对应的移动站的已知位置，将式（15）代入式（16）即可得到移动站的位置。

4 仿真结果

本文采用微小区模型，如图1，该模型同样用在文献[3]中，本文仿真环境参照文献[3]中的设定，一共五个基站，如图1中黑点所示，为楼群区，两条街道的长度为600m，宽度为20m。无线电波由均匀分布在图1中菱形部分的移动站开始，在阴影区域楼群区的拐角处发生折射，最后终止于基站，即基站到移动站无线电波的传输距离为d_c+d_r，在此传播路径中，噪声服从零均值高斯分布。

本文采用文献[3]中给出了h_z的最优取值为3.6σ，本文提出的基于Kriging插值的非参数核方法将与文献[3]中不进行插值的非参数核方法，参数化的最小二乘方法以及CRLB下限做比较。

图2是在10m的距离测量噪声标准差以及事先知道样本点数量为20的情况下，两种算法的性能比较图。由于文獻[3]中的非参数核方法没有进行插值，随着插值点个数U的变化，理论上定位误差是保持不变的，然而由于距离测量噪声和已知样本点的分布是随机的，因此其定位误差存在一定波动性。可以看出文献[3]中随着插值点个数U的变化，非参数核方法的定位性能在总体上是平稳的，而本文算法的定位误差在U增大过程中逐渐减小，当多于100个插值点时，算法性能逐于稳定，且本文算法明显优于文献[3]算法。

图3是在10m的距离测量噪声标准差以及U=200情况下，两种算法的误差比较图，由图可得，在已知样本点个数逐渐增加过程中，两种算法的定位精度都在提高，但本文算法始终优于文献[3]算法，特别是在小样本条件下，本文算法优势更为明显，当文献[3]中所需要55个已知采样点才能到达25m的定位精度时，本文算法只需要15个已知采样点，这样大幅度减少已知采样点的个数，从而减少获取这些采样点的成本，提高算法定位精度及实用性。

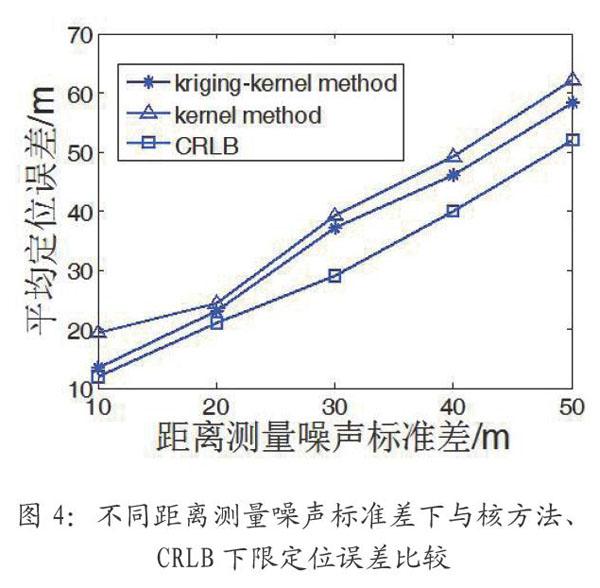
图4是在已知100个样本点和U-200条件下，两种算法在不同距离测量噪声标准差情况下定位误差与CRLB下限做比较图，由图可得，两种算法都逼近CRLB下限，但是本文算法更接近CRLB下限，也即优于文献[3]算法。同时相同条件下，本文算法与最小二乘方法的定位误差进行比较，也得本文算法优于最小二乘方法。

5 结论

本文提出基于Kriging数据插值的非参数核方法，该方法首先扩展样本点集合，即使用Kriging对事先知道的样本点集合进行插值，再使用扩展后的样本点集合进行定位，使得算法能有效利用样本信息，仿真表明本文算法性能优于不进行插值的非参数核方法，算法性能更为接近CRLB下限，特别是在小样本条件下，优势更为明显，这样就减少了已知采样点的个数，从而降低定位成本，增强算法实用性。

参考文献

[1]饶中初，黄际彦.一种新的非直达波传播环境下的TDOA定位方法[J].电子对抗，2015（04）：13-16.

[2]万群，王军，罗咏劼，等.抑制非直达波误差的高阶矩方法[J].电子学报，2005，33（10）：1822-1824.

[3]Mcguire M，Plataniotis K N，Venetsanopoulos A N.Locationof mobile terminals using timemeasurements and survey points[J].IEEE Transactions on VehicularTechnology，2003，52（04）：999-1011.