含切口复合材料层合板拉伸应变集中与失效分析
2018-02-28贾普荣
王 刚,贾普荣,黄 涛,张 龙
(西北工业大学 力学与土木建筑学院,西安 710129)
近年来,复合材料在航空航天领域的应用日益广泛,已成为飞机制造中重要的结构材料之一。由于结构设计和连接的需要,有必要对复合材料板加工切口。但是,复合材料切口会导致局部纤维切断,降低了其刚度和强度,切口引起的局部应变集中也会引起层合板提前发生失效[1]。因此,研究含切口复合材料的损伤破坏问题具有重要的工程意义。
国内外许多研究者对含切口复合材料的力学行为展开了研究。Tan[2]建立了含椭圆形切口的正交各向异性复合材料层合板的应力近似分析方法,朱西平等[3]基于应力近似计算方法分析了材料性能、铺层方式等因素对复合材料层合板的孔边应力集中的影响。对于含切口复合材料层合板的强度问题,Whitney等[4]提出的点应力准则和平均应力准则可用于估算含有中心切口复合材料层合板的剩余强度,但不能描述层合板的损伤进程。Lapczyk等[5]建立了基于应变能耗散的三角形线性应变软化模型,结合Hashin失效准则分析了含圆形切口的纤维-金属层合板的损伤演化过程。Camanho等[6]通过实验研究了宽径比为6时圆形切口对层合板剩余强度的影响,并基于连续介质损伤力学模型对圆形切口复合材料层合板试件拉伸损伤过程进行了数值模拟。Chen等[7-8]提出了一种基于弹塑性本构关系的渐进失效分析方法对开孔层合板损伤过程进行分析,Qing等[9]提出基于物理失效机制的复合材料三维各向异性损伤模型,预测了不同铺层方式的开孔层合板拉伸和压缩强度。在国内,郭洪宝等[10]对双边开半圆形切口、V形切口和细线形切口的C/SiC复合材料拉伸强度和失效过程进行了对比分析,李亮等[11]对含有长条形切口复合材料层合板的拉伸失效行为进行了实验研究,得到了切口长度和角度对剩余强度的影响规律,并验证了基于等效刚度的强度模型用于描述含切口复合材料层合板拉伸失效行为的可行性。李彪等[12]建立了考虑就地效应的复合材料层合板的强度分析模型,吴义韬等[13]采用CDM模型预测了复合材料开孔层合板的强度,黄河源等[14]通过对比实验和数值模拟结果讨论了不同刚度退化模型对复合材料大开口结构的强度预测精度问题。
从目前研究可见,针对不同切口形式对复合材料层合板拉伸应变集中与损伤进程影响的研究较少。基于复合材料的实际应用情况,本工作设计并开展了试件中心含圆形切口和长条形切口复合材料层合板的拉伸实验,并结合渐进损伤分析模型对两种含切口复合材料层合板的应变集中现象和损伤破坏规律进行了研究。
1 实验
1.1 含切口复合材料层合板试件

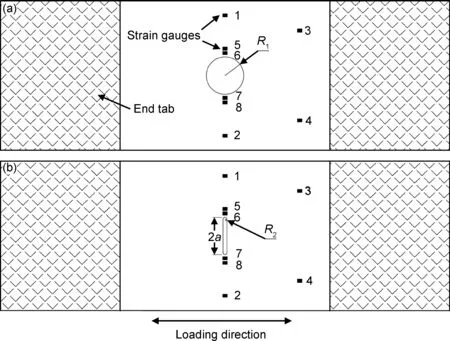
图1 含切口复合材料层合板拉伸试件及应变片粘贴位置 (a)圆形切口;(b)长条形切口Fig.1 Notched specimens of composite laminates and location of strain gauges (a)circular notch;(b)oblong notch
1.2 含切口复合材料层合板拉伸实验
两种含切口复合材料层合板拉伸实验均在CSS-WAW-600液压万能试验机上完成。采用位移控制方式加载,加载速率为1.25mm/min。如图1所示,在试件中间部位上距离切口前缘2mm(6#,7#),4mm(5#,8#)和距试件边缘10mm(1#,2#)处对称粘贴应变片,用于监测加载过程中试件缺口位置附近的应变响应。在距试件切口截面50mm、边缘20mm(3#,4#)处贴有一对应变片,用于监测试件的远场应变。在实验过程中,采用DH3815型多通道应变采集系统记录应变随载荷的变化状态。
2 实验结果与分析
根据实验机记录的载荷和试件尺寸计算层合板的名义应力σN,计算公式如下:
(1)
式中:P为实验测得的载荷;w为试件宽度;b为试件厚度。名义尺寸为:w=100mm,b=4.5mm。
各个应变片测试点的应变随名义应力的变化规律如图2所示。可以看出,在远离切口位置处,即1#,2#测点与3#,4#测点所测得的应变较为接近;在切口附近位置的测点应变均明显大于远场应变,表明切口引起了层合板的局部应变集中。对比同等应力水平下两种含切口试件相同位置的应变可知,两种不同形式切口引起的应变集中程度有较大差异。由于切口引起了复合材料层合板的局部应变集中,远场应变更能代表复合材料层合板沿加载方向的平均应变状态,两种含切口复合材料层合板试件的典型远场应变-名义应力曲线如图3所示。两种含切口复合材料层合板试件的远场应变-名义应力曲线斜率较为接近,说明两种含切口复合材料层合板的名义拉伸弹性模量几乎相同。

图2 含切口复合材料层合板拉伸试件应变-应力曲线 (a)圆形切口;(b)长条形切口Fig.2 Stress-strain curves of notched specimens of composite laminates (a)circular notch;(b)oblong notch

图3 含切口复合材料层合板拉伸试件远场应变-名义应力曲线Fig.3 Far-field strain-nominal stress curves of notched specimens of composite laminates
根据加载过程中应变片数值的变化规律可知,长条形切口试件比圆形切口试件率先发生切口附近的局部损伤失效。当切口附近局部出现损伤时,切口前沿区域发生载荷重新分配,继续加载则出现损伤扩展,离切口较远的区域也逐渐发生破坏,直至试件达到极限强度。由圆形切口试件测得的应变数据变化规律表明,圆形切口试件的局部失效与整体失效具有较高的同步性,试件破坏前无明显损伤。测试结果说明圆形切口附近发生局部损伤失效时,试件有效截面上的平均应力已达到层合板强度值,缺口前沿韧带区已无法承担更高的载荷,层合板随即发生整体破坏。
由拉伸破坏实验得到两种含切口复合材料层合板试件的损伤断裂状态,破坏形貌如图4所示。测得的两组试件名义拉伸强度及离散系数见表1,经过对比发现,虽然两组试件的应变集中系数不同导致应变分布不一致,且损伤破坏过程有较明显的区别,但两组试件的名义拉伸强度较为接近,圆形切口试件的名义拉伸强度略高于长条形切口试件强度。

图4 含切口复合材料层合板拉伸试件断裂形貌 (a)圆形切口;(b)长条形切口Fig.4 Fracture appearance of notched specimens of composite laminates (a)circular notch;(b)oblong notch

表1 含切口复合材料层合板拉伸实验结果Table 1 Experimental results of notched composite laminates under tensile loading
3 渐进损伤分析
3.1 失效准则
为了进一步研究两种含切口复合材料层合板的损伤破坏规律,采用渐进损伤分析方法对含切口复合材料层合板的拉伸失效行为进行模拟分析,计算可得含切口复合材料层合板在面内拉伸载荷下的损伤进程及极限载荷。
复合材料单层失效模式分为纤维控制失效模式和基体控制失效模式[15-16],具体表现为纤维拉伸断裂、纤维压缩屈曲折断,基体拉伸或压缩失效,以平面应变表示的失效模式如下[17]:
(1)纤维控制失效模式:
(2)
(2)基体控制失效模式:
(3)

3.2 损伤演化准则
渐进损伤分析中,当模型某点材料满足初始失效准则后,需对材料属性进行退化。目前,用于复合材料渐进损伤分析中的材料属性折减方法主要有:(1)瞬时刚度退化模型;(2)阶梯刚度退化模型;(3)连续刚度退化模型。相关文献[13-14,18-20]的计算结果表明,这三种刚度退化模型均能较准确的预测层合板的承载能力。文献[13]对比了这三种刚度折减方法,通过计算得到了复合材料开口结构强度,并发现连续刚度退化模型计算结果与实验结果最为接近。
本工作选取指数形式的连续刚度退化模型对损伤材料单元进行刚度折减,引入损伤变量df和dm描述复合材料层合板单层沿纤维方向和垂直于纤维方向的损伤状态,用式(4)和式(5)表示为[9]:
(4)
(5)
式中:Gf和Gm分别为复合材料层合板单层沿纤维方向和垂直于纤维方向的断裂能;L为单元特征长度。当ε11>0时,XT(C)=XT;ε11<0时,XT(C)=XC;当ε22>0时,YT(C)=YT;ε22<0时,YT(C)=YC。
计算模型中,将应力分量和应变分量用矩阵表示为:σ=[σ11σ22σ33τ12τ13τ23]T,ε=[ε11ε22ε33γ12γ13γ23]T。当单元发生损伤时,含损伤材料的刚度矩阵Cd用式(6)表示[21],即:
(6)
式中:α=1-df,β=1-dm,Cij为无损材料的刚度系数。将失效单元的应力更新为:
σ=Cdε
(7)
上述渐进损伤分析模型通过在商用有限元软件ABAQUS中使用UMAT用户子程序实现。
3.3 含切口复合材料层合板有限元模型
根据含切口复合材料层合板的几何特征和铺层顺序,分别建立图5所示的含圆形切口和长条形切口的复合材料层合板三维有限元模型,在厚度方向上每层为一个单元,单元类型为C3D8R。由于切口会引起应力集中,对切口周围进行网格细化。在模型右端建立参考点(RP),并对参考点和右端面建立多点约束,用于对模型进行加载和输出载荷。对模型左端面施加位移约束Ux=0,对参考点施加沿x轴方向的位移,实现对模型的拉伸加载。复合材料单层板为正交各向异性材料,在有限元模型中根据试件铺层顺序对各单层赋予材料主方向,材料属性如表2所示。

图5 含切口复合材料层合板有限元模型 (a)圆形切口;(b)长条形切口Fig.5 Finite element models of notched composite laminates (a)circular notch;(b)oblong notch

表2 CYCOM X850-35-12K IM+-190复合材料属性Table 2 Mechanical properties of CYCOM X850-35-12K IM+-190 composites
通过渐进损伤分析得到了含切口复合材料层合板在拉伸载荷下的应力和应变场。提取应变片粘贴区域单元应变的平均值,以及应变随名义应力的变化规律。两种含切口复合材料层合板的拉伸模拟结果与实验结果对比如图6所示。对比可知,有限元分析得到的各测点应变随名义拉伸应力的变化规律与实验结果吻合较好。从应变的变化规律可以看出,长条形切口复合材料层合板切口附近的应变片(5#,6#)粘贴区域在较低应力下率先发生失效,圆形切口复合材料层合板切口附近应变片(5#,6#)粘贴区域在试件临近极限载荷时才发生失效。

图6 含切口复合材料层合板板试件拉伸应力-应变曲线 (a)圆形切口;(b)长条形切口Fig.6 Stress-strain curves of notched composite laminates under tensile loading (a)circular notch;(b)oblong notch
渐进损伤分析中,圆形切口复合材料层合板名义应力达到259.6MPa和275.7MPa时,90°层和±45°层先后发生基体初始损伤,名义应力达到355.9MPa时,中间0°层率先发生纤维初始损伤。长条形切口复合材料层合板名义应力达到113.1MPa时,90°层和±45°层发生基体初始损伤,名义应力达到157.3MPa时,中间0°层率先发生纤维初始损伤。对比可知,长条形切口复合材料层合板各层发生初始损伤的载荷均低于圆形切口复合材料层合板的载荷。
复合材料层合板受拉伸载荷时各层共同承担载荷,其中纤维承担主要作用。取中间0°层发生纤维初始损伤时的应变云图,如图7所示。对比可知,虽然长条形切口试件的0°层在较低载荷下率先发生损伤,此时远场应变为0.19%,最窄净截面总体上仍处于较低应变水平,切口前缘发生损伤后载荷重分配能力较强,损伤逐渐向试件边缘扩展。对于圆形切口试件,临近层合板整体失效时0°层才发生初始损伤,此时远场应变为0.45%,最窄净截面上总体已处于较高应变水平,切口附近的材料应变已接近破坏应变,层合板随后发生整体破坏。
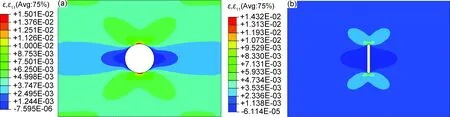
图7 0°层发生初始损伤时的应变状态 (a)圆形切口;(b)长条形切口Fig.7 Strain distribution of 0° ply at failure initiation (a)circular notch;(b)oblong notch
数值分析得到的含切口复合材料层合板试件拉伸名义强度和实验结果如表3所示,二者吻合较好。结合图6所示的测点应变的变化规律可知,该渐进损伤模型可准确分析含切口复合材料层合板试件的拉伸力学行为。

表3 含切口复合材料层合板名义拉伸强度实验结果与数值模拟结果Table 3 Experimental and numerical nominal tensile strength of notched composite laminates
含切口复合材料层合板名义应力达到最大值时各层的损伤云图如图8所示,红色区域和蓝色区域分别代表损伤区域和未损伤区域。可以看出,90°层损伤以基体控制的损伤模式为主,其他铺层的损伤都伴随有纤维失效和基体失效。层合板切口前缘发生初始损伤后,损伤逐渐向外扩展。名义应力达到最大时,长条形切口板的损伤区域大于圆形切口板。

图8 含切口复合材料层合板达到极限载荷时损伤云图Fig.8 Damage patterns of notched composite laminates at the ultimate load
3.4 应变集中分析
为进一步分析切口引起的局部应变集中现象,提取有限元分析得到的层合板应变状态。由于切口前缘发生损伤后会改变应变分布,在计算结果中读取有限元模型加载到名义应力为90MPa时的应变状态(此时层合板均未发生损伤),分别得到两种含切口复合材料层合板最窄截面上各点沿加载方向的应变随着离试件中心距离的变化规律,如图9所示。
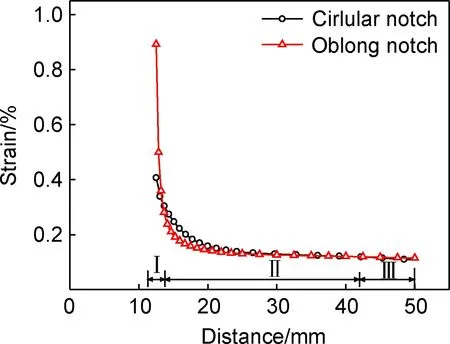
图9 最窄截面上的应变分布Fig.9 Strain distribution along the narrowest section
根据图9所示的应变分布规律,可将最窄截面分为三个区域。切口前缘区域(Ⅰ),长条形切口板的应变水平较高;离切口较远的区域(Ⅱ),圆形切口板的应变水平较高;而靠近试件边缘区域(Ⅲ),两者的应变水平逐渐趋于一致。实验过程中,5#,6#,7#,8#应变片分布于Ⅱ区域,1#和2#应变片分布于Ⅲ区域,图3所示的实验测得的应变分布与此处得到的应变分布规律有较好的一致性。
从图9可以看出,相对于圆形切口,长条形切口引起的切口尖端应变集中系数较高,但应变分布梯度较大,这使得长条形切口试件率先发生局部失效,但剩余承载面处于较低应变水平,载荷重分配能力较强,这是两种含切口复合材料层合板拉伸强度接近的原因。
4 结论
(1)圆形切口和长条形切口引起了层合板不同程度的应变集中,长条形切口引起的应变集中系数较高,但切口前缘的应变分布梯度更大。
(2)两种含不同形式切口的层合板损伤进程有明显区别,但二者拉伸强度相差不大,这与切口引起的应变集中系数和应变分布梯度有关。
(3)渐进损伤分析得到的两种切口试件应力-应变曲线及强度值与实验结果吻合较好,说明该模型可准确分析含切口层合板在面内拉伸载荷下的损伤破坏规律。
(4)对于不同的板宽与切口尺寸的比值,切口形式对层合板剩余拉伸强度的影响还有待进一步研究。
[1] WANG J, CALLUS P J, BANNISTER M K. Experimental and numerical investigation of the tension and compression strength of un-notched and notched quasi-isotropic laminates[J]. Composite Structures, 2004, 64(3/4): 297-306.
[2] TAN S C. Stress concentrations around holes[M]. Lancaster: Technomic, 1994.
[3] 朱西平, 郭章新, 韩小平, 等. 含孔复合材料层合板孔边应力集中的近似计算[J]. 航空材料学报, 2009, 29(2): 71-75.
ZHU X P, GUO Z X, HAN X P, et al. Approximate calculation of stress distribution near hole for composite laminates with finite width[J]. Journal of Aeronautical Materials, 2009, 29(2): 71-75.
[4] WHITNEY J M, NUISMER R J. Stress fracture criteria for laminated composites containing stress concentrations[J]. Journal of Composite Materials, 1974, 8: 253-265.
[5] LAPCZYK I, HURTADO J A. Progressive damage modeling in fiber-reinforced materials[J]. Composites Part A: Applied Science and Manufacturing, 2007, 38(11): 2333-2341.
[6] CAMANHO P P, MAIMI P, DAVILA C G. Prediction of size effects in notched laminates using continuum damage mechanics[J]. Composites Science and Technology, 2007, 67(13): 2715-2727.
[7] CHEN J F, MOROZOV E V, SHANKAR K. A combined elastoplastic damage model for progressive failure analysis of composite materials and structures[J]. Composite Structures, 2012, 94(12): 3478-3489.
[8] CHEN J F, MOROZOV E V, SHANKAR K. Simulating progressive failure of composite laminates including in-ply and delamination damage effects[J]. Composites Part A: Applied Science and Manufacturing, 2014, 61: 185-200.
[9] QING H, MISHNAEVSKY L. 3D constitutive model of anisotropic damage for unidirectional ply based on physical failure mechanisms[J]. Computational Materials Science, 2010, 50(2): 479-486.
[10] 郭洪宝, 王波, 矫桂琼, 等. 2D-Cf/SiC复合材料缺口试件拉伸力学行为研究[J]. 材料工程, 2013(5): 83-88.
GUO H B, WANG B, JIAO G Q. et al. Tensile mechanical behavior of notched 2D-Cf/SiC composites[J]. Journal of Materials Engineering, 2013(5): 83-88.
[11] 李亮, 贾普荣, 黄涛, 等. 含切口损伤复合材料层合板拉伸失效行为研究[J]. 固体力学学报, 2015, 36(2): 137-144.
LI L, JIA P R, HUANG T, et al. Study in the failure behavior of notched composite laminate under tensile load[J]. Chinese Journal of Solid Mechanics, 2015, 36(2):137-144.
[12] 李彪, 李亚智, 杨帆. 考虑复合材料层合板就地效应的强度理论[J]. 航空学报, 2014, 35(11): 3025-3036.
LI B, LI Y Z, YANG F. Theoretical methodology for laminated composite strength includingin-situeffect[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 3025-3036.
[13] 吴义韬, 姚卫星, 吴富强. 复合材料层合板面内渐进损伤分析的CDM模型[J]. 力学学报, 2014, 46(1): 94-104.
WU Y T, YAO W X, WU F Q. CDM model for intralaminar progressive damage analysis of composite laminates[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 94-104.
[14] 黄河源, 赵美英, 王文智, 等. 复合材料三维损伤模型在大开口结构强度预测中的应用[J]. 复合材料学报, 2015, 32(3): 881-887.
HUANG H Y, ZHAO M Y, WANG W Z, et al. Application of three-dimensional damage model in the strength of large opening composite material structures[J]. Acta Materiae Compositae Sinica, 2015, 32(3): 881-887.
[15] HASHIN Z, ROTEM A. A fatigue failure criterion for fiber-reinforced composite materials[J]. Journal of Composite Materials, 1973, 7: 448-464.
[16] HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2): 329-334.
[17] 王文智, 万小朋, 姚辽军. 基于CDM的开口复合材料层合板结构损伤研究[J]. 航空工程进展, 2013(3): 285-291.
WANG W Z, WAN X P, YAO L J. Damage and failure study of composite laminates with reinforced cutout based on CDM[J]. Advances in Aeronautical and Engineering, 2013(3): 285-291.
[18] 王跃全, 童明波, 朱书华. 三维复合材料层合板渐进损伤非线性分析模型[J]. 复合材料学报, 2009, 26(5): 159-166.
WANG Y Q, TONG M B, ZHU S H. 3D nonlinear progressive damage analysis model for composite laminates[J]. Acta Materiae Compositae Sinica, 2009, 26(5): 159-166.
[19] SU Z C, TAY T E, RIDHA M, et al. Progressive damage modeling of open-hole composite laminates under compression[J]. Composite Structures, 2015, 122: 507-517.
[20] QU P, SUN X, GUAN X, et al. Effect of interlaminar toughness on the low-velocity impact damage in composite laminates[J]. Polymer Composites, 2016, 37(4): 1085-1092.
[21] LINDE P, PLEITNER J, BOER H D, et al. Modelling and simulation of fiber metal laminates [C]∥Boston, Massachustts: ABAQUS User’s Conference, 2004: 421-439.
