一种基于泰勒级数展开的电离层延迟改正模型

张兆龙，王跃钢，腾红磊，王 乐

(火箭军工程大学，陕西 西安 710025)

距地球表面高度50～1000 km的大气层称为电离层，电离层中的气体分子由于受到辐射而产生电离[1]。当卫星信号通过电离层时，信号的传播路径和速度会发生变化，因此计算所得的卫星至接收机的几何距离与真实值之间存在偏差，对观测量造成影响，称为电离层延迟[2-3]。

在卫星导航定位中，电离层延迟是主要的误差源之一，很大程度上影响了定位的精度和准确度[4-5]。针对电离层延迟误差问题，国内外的众多学者和机构进行了大量的研究并取得了丰富的成果。对于单频接收机定位而言，由于不能消除一阶电离层延迟，因此采用电离层模型来进行误差改正[6-7]。一般是应用卫星播发的导航电文中的电离层延迟改正参数，因此电离层延迟改正参数的精度直接影响接收机的定位精度[8]，提高电离层延迟改正模型的精度是当前研究的重点，也是进一步提高定位精度的需求[9]。本文提出一种基于泰勒级数展开的电离层延迟改正模型(TSE模型)，通过试验仿真分析，并与Klobuchar模型和NeQuick模型进行对比，以验证该模型在一定程度上提高电离层延迟改正误差和区域上的时间适应度的能力。

1 电离层延迟改正模型

1.1 Klobuchar模型

Klobuchar模型是一种广泛应用于单频接收机定位的传统电离层延迟改正模型，该模型采用余弦函数解算电离层延迟，包括8个直观简洁的参数。大量试验研究表明，Klobuchar模型的改正效果一般在60%左右，改正精度较低，其表达式如下[10-11]

(1)

式中，DC为晚间电离层延迟量，通常取DC=5 ns；t0为最大电离层延迟所对应的地方时；Tp=14 h50 400 s；P为电离层延迟函数周期，单位为s；A为电离层延迟函数振幅，单位为s。其表达式可表示为

(2)

(3)

式中，αi和βi为导航电文所提供的改正参数；φm为穿刺点的地磁纬度；t为穿刺点的地方时。具体的计算步骤见文献[12]。

1.2 NeQuick模型

NeQuick模型是一个随时间变化的三维电离层电子密度模型。相关研究表明，该模型的改正精度较Klobuchar模型较高，但是结构较复杂，在运算过程中涉及数值积分，时效性较差[13-14]。其基本表达式如下

(4)

式中，N表示电子密度；h为所求点的高度；Nmax是Epsterin层的电子密度峰值；hmax表示Epsterin层的电子密度峰值点的高度；B为Epsterin层的厚度参数。

1.3 TSE模型

泰勒级数是无限项连加的特定函数的数学描述，这些相加的项由该函数在某一点的导数计算所得[15]。本文所提出的模型正是利用泰勒级数展开，且将整个电离层简化为单层模型，该单层电离层称为中心电离层或平均电离层，而后进行电离层延迟改正。

TSE电离层延迟改正模型可描述为

(5)

其中

β=βIP-β0

(6)

S=SIP-S0

(7)

式中，βIP和SIP分别表示在日固地理坐标系下电离层穿刺点(IPP)的纬度和经度；β0和S0表示扩展原始坐标；n和m分别表示纬度和经度的泰勒级数展开阶数；nmax和mmax分别表示纬度和经度泰勒级数展开的最大阶数；Cnm是未知系数。电离层穿刺点(IPP)的纬度和经度计算方式如下

βIP=arcsinsinφkcosα+cosφksinαcosθa

(8)

(9)

式中，φk和λk分别表示接收机k的纬度和经度；θa表示接收机和可见卫星之间的方位角；α是地球中心分别与接收机和电离层穿刺点连线之间的夹角[16]。单层电离层模型如图1所示。

电离层延迟可表示为

(10)

式中，F为依赖于高程的映射函数

(11)

f1是GPS载波L1的频率，其频率为1 575.42 MHz；Z′为电离层穿刺点处的卫星的天顶角，可表示为

(12)

式(8)中，Re=6 378.1 km，为地球平均半径，H=350 km，为单层电离层薄壳的高度；z为接收机的天顶角。将式(5)代入式(10)可得

(13)

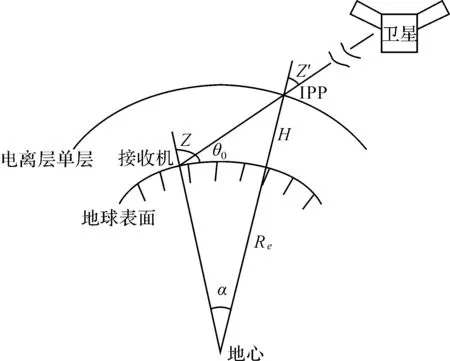
图1 单层电离层模型

因此，对于可见星p=1,2,…,ns和接收机k，电离层延迟δIk为

(14)

式中

(15)

(16)

(17)

式中，Ak为泰勒级数展开的几何矩阵；nmax和mmax为泰勒级数展开的阶数，且ns>Xc。矩阵Ak中包含所有可见星的电离层穿刺点的纬度和经度值，矩阵Xc中的各个量为未知系数(C00到Cnm)，从几何矩阵和测量数据(VTEC)中可以求得这些未知系数。求解过程如下：取nmax=mmax=2，β0=S0=0，令Y=AkXc，其中，矩阵Y为实测VTEC数据，假设某一位置在某一时刻的可见星为10颗，数据采样间隔为5 min，则可求得TSE模型中的9个未知系数，Y、Ak和Xc可分别表示为

(18)

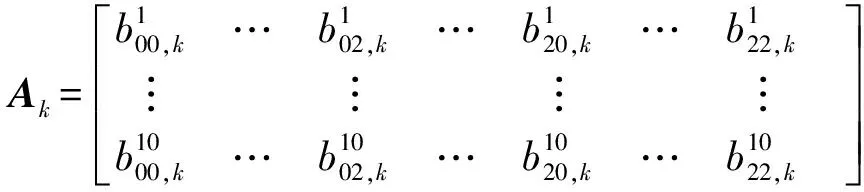
(19)

(20)

运用最小二乘法，则未知系数矩阵Xc为

(21)

将式(21)计算得到的Xc代入式(14)，则可得电离层延迟改正误差。

2 试验仿真及结果分析

为评估TSE模型对电离层延迟的改正效果以及比较不同电离层改正模型对单频精密单点定位精度的影响，试验方案如下：

(1) 方案1：采用IGS中国站BJFS(北京房山)站点的观测数据，选取太阳活动低年2009年第218天和太阳活动高年2012年第115天的数据进行仿真，分别求得3种模型VTEC计算值与参考值之间的均方差RMS，结果如图2所示。

从图2可以看出，在2009年第218天，即太阳活动低年，Klobuchar模型的RMS较大，NeQuick模型和TSE模型的RMS不超过3 TECU，可以较好地反映电离层的变化情况，但是TSE模型的RMS总体趋势更平稳，精度更高。在2012年第115天，即太阳活动高年，3个模型的RMS较2009年第218天(太阳活动低年)略高，TSE模型的RMS比其他两个模型都要小。综上所述，说明TSE模型的VTEC计算值与参考值之间的偏差不大，基本一致，其在提高改正精度上是可行的，且在不同时间(太阳活动高低年)都有较强的适应性。

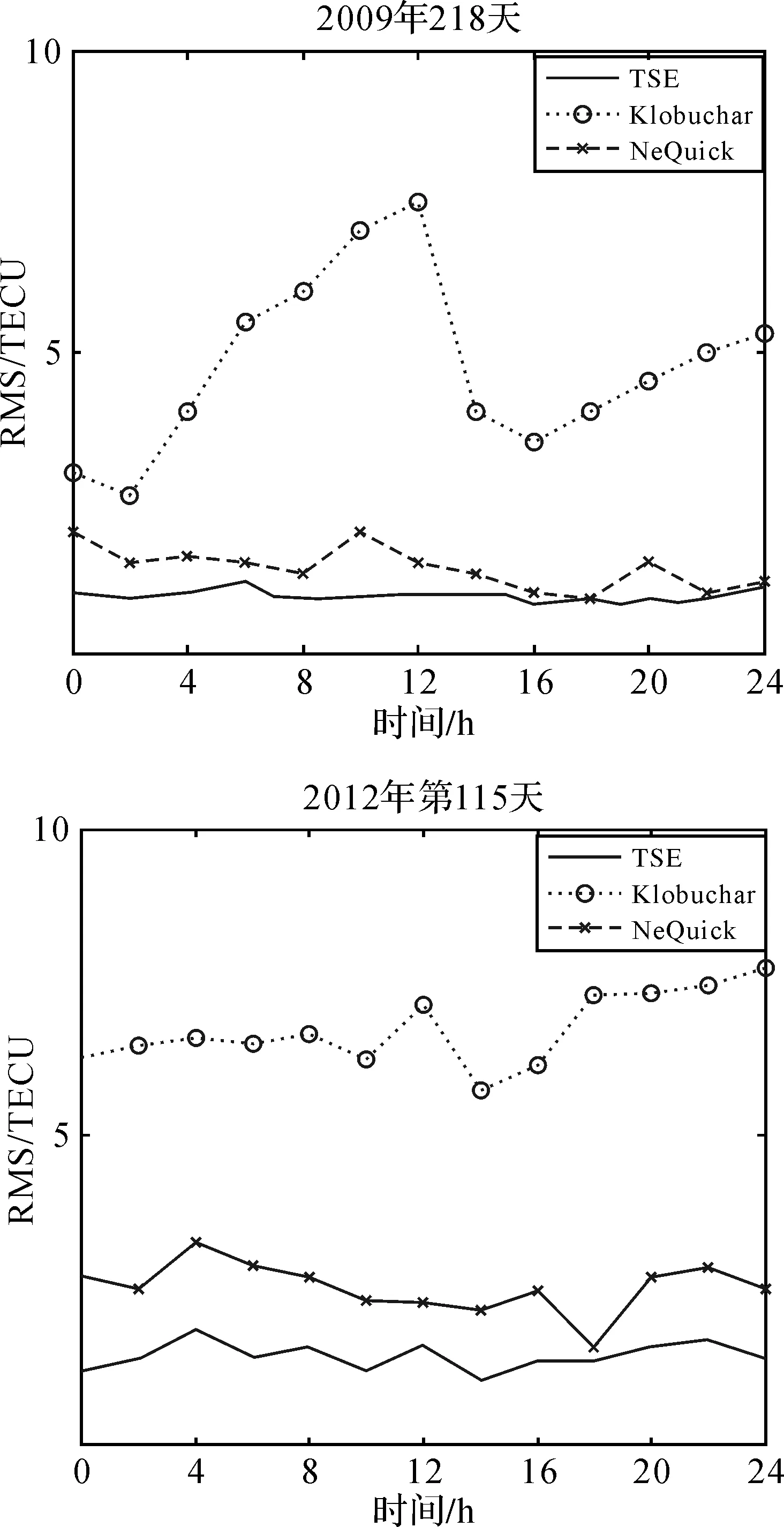
图2 Klobuchar模型、NeQuick模型、TSE模型所求VTEC的RMS比较

(2) 方案2：采用IGS中国站BJFS(北京房山)站点2009年1月1日的观测值，用单点定位进行位置解算时，分别采用Klobuchar模型、NeQuick模型、TSE模型3种不同的电离层改正模型，将解算所得的测站坐标与IGS公布的当天坐标值进行对比，结果如图3—图5所示。

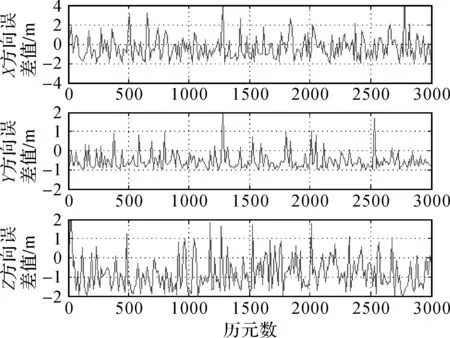
图3 Klobuchar模型改正电离层延迟的定位误差

图4 NeQuick模型改正电离层延迟的定位误差

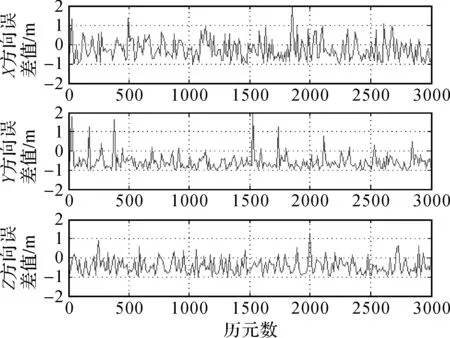
图5 TSE模型改正电离层延迟的定位误差

由图3—图5可以看出，在单频精密单点定位中，电离层延迟误差改正采用TSE模型的定位精度要优于采用Klobuchar模型和NeQuick模型，其中，Klobuchar模型的定位精度最差且波动较大。采用TSE模型进行解算的测站位置在X、Y、Z方向上与参考值之间的误差范围在1 m以内，即定位精度约为1 m，表明了TSE模型在一定程度上提高了单点定位精度的可行性。

3 结 语

在单频精密单点定位中，电离层延迟是一项重要的误差源，电离层延迟误差改正精度的提高对定位精度的提高具有重要的意义。通过仿真试验验证，本文研究探讨的基于泰勒级数展开的电离层改正模型在提高定位精度上有一定有效性和可行性，且有较强的时间适应性。

[1] 郑建雷, 黄张裕, 刘国超. 单频精密单点定位中电离层延迟改正方法[J]. 测绘与空间地理信息, 2015, 38(2): 144-146.

[2] SHI Chuang，GU Shengfeng，LOU Yidong，et al. An Improved Approach to Model Ionospheric Delays for Single-frequency Precise Point Positioning[J]. Advances in Space Research, 2012, 49(12): 1698-1708.

[3] 康娟. 全球卫星导航系统电离层建模方法研究[D]. 长沙: 湖南大学, 2015.

[4] 杨新文, 杨徉. 一种基于卫星穿刺点位置的区域电离层增强方法[J]. 测绘通报, 2016(11): 5-8.

[5] ZHANG Rui，SONG Weiwei，YAO Yibin，et al. Modeling Regional Ionospheric Delay with Ground-based BeiDou and GPS Observation in China[J]. GPS Solutions, 2015,19(4): 649-658.

[6] 李强，宁百齐，赵必强，等. 基于陆态网络GPS数据的电离层空间天气监测与研究[J]. 地球物理学报, 2012, 55(7): 2193-2202.

[7] 田英国, 郝金明, 于合理，等. LEO卫星单频精密定轨电离层模型改进算法[J]. 测绘学报, 2016, 45(7): 803-809.

[8] 袁运斌, 欧吉坤. GPS 观测数据中的仪器偏差对确定电离层延迟的影响及处理方法[J]. 测绘学报,1999, 28(2): 110-114.

[9] 王斐, 吴晓莉, 周田, 等. 不同Klobuchar模型参数的性能比较[J], 测绘学报, 2014, 43(11): 1151-1157.

[10] 徐李冰, 蔡成林, 陈光喜, 等. 一种新的北斗Klobuchar模型及其精度分析[J]. 大地测量与地球动力学, 2015, 35(5): 788-792.

[11] 涂锐, 黄观文, 张勤. GPS单频机电离层延迟改正新算法[J]. 武汉大学学报(信息科学版), 2012, 37(6): 667-670.

[12] 崔敬. GPS单频精密单点定位的电离层延迟改正研究[D]. 北京: 中国地质大学, 2013.

[13] 吴宇航, 陈秀万, 吴才聪，等. 电离层延迟修正方法评述[J]. 全球定位系统, 2008, 33(2): 1-5.

[14] TAO Anlin，JAN Shaushiun. Wide-area Ionospheric Delay Model for GNSS Users in Middle and Low-magnetic-latitude Regions[J]. GPS Solutions, 2015, 20(1):1-13.

[15] KUMAR P N,SARMA A D，REDDY A S.Modeling of Ionospheric Time Delay of Global Positioning System(GPS)Signals Using Taylor Series Expansion for GPS Aided Geo Augmented Navigation Application[J]. Radar Sonar and Navigation Let, 2014, 8(9): 1081-1090.

[16] 李志刚, 程宗颐, 冯初刚，等. 电离层预报模型研究[J]. 地球物理学报, 2007, 50(2): 327-337.