基于土壤变异解释力的几种土壤制图方法的对比研究*——以南阳市1m土体土壤有机碳密度制图为例

赵彦锋 李豪杰 陈 杰 孙志英 梁思源

（1 郑州大学水利与环境学院地理信息科学系，郑州 450001）

（2 河南省国土资源调查规划院，郑州 450016）

（3 郑州大学公共管理学院，郑州 450001）

由于土壤—成土因子之间的多尺度、非线性关系，基于詹尼方程和传统数学预测土壤属性具有较大局限性；1950—2000年，假设土壤类型与其属性的对应关系，土壤类型连接法是进行土壤有机碳密度（Soil organic carbon density，SOCD）和碳储量估算的常用方法［1-7］。随着现代数学发展，以及数字高程、遥感等制图辅助变量的类型日益广泛和易得，以数字土壤制图（Digital soil mapping，DSM）方式进行土壤有机碳密度制图和储量估算成为主流。当前，土壤有机碳的DSM方法总体分为三类［8］：第一，纯粹的空间方法，即地统计学方法。第二，确定性关系建模方法。最初这类方法主要指线性回归，现在则广泛地包括空间地理回归、人工神经网络、回归树等现代数学方法［9-16］。第三，混合模型方法。混合模型主要是回归克里格概念的延伸：回归可以是线性回归，也可以是以土壤或土地类型单元提取的趋势（均值或中值），也可以是各种机器学习算法的结果。也即在各种算法基础上，对预测残差进一步应用克里格插值的方法均被称为回归克里格［17-20］。

尽管土壤有机碳的DSM技术发展较快，但由于大空间尺度土壤碳密度的影响因素复杂，同时由于剖面深层土壤碳密度与地形、遥感等环境协变量的关系减弱［21-22］，使得1m土体碳密度制图的DSM模型并不总能取得理想精度。因此，土壤类型连接法在大、中尺度土体的碳密度制图方面仍具有较强的实践价值［23］。同时，土壤类型连接法在土壤碳密度制图和碳储量估算方面已取得不少成果，应将其与DSM法系统对比，以便更加客观看待之。对于现有的DSM方法而言，一些比较研究中强调模型法较克里格法有效［24］，或者回归克里格方法能有效结合模型方法和空间方法的优势等［16-19］。Brungard等［25］比较11种机器学习算法，发现随机森林、人工神经网络、支持向量机等复杂的建模方法一般优于k临近距离、多元逻辑回归等简单建模方法。显然，上述研究者倾向于认为更复杂和精密的方法对提高土壤制图效果具有重要意义，但该观点并不全面。如Heung等［26］比较了10种机器学习算法在数字土壤制图中的效果，发现k邻近距离法和支持向量机法优于人工神经网络和随机森林等其他方法；而Taghizadeh-Mehrjardi等［27］在类似的研究中表明人工神经网络和决策树法优于支持向量机、K邻近距离和随机森林；上述结论存在矛盾之处。一些研究认识到研究条件对结果的制约，如对于不同类型区或者参数组合不同，随机森林方法效果差异较大；而Martin等［15］发现当更有效的土壤有机碳驱动因子被代入BRT（Boosted regression trees，BRT）模型，再进行残差克里格的实际意义不大。

可见，土壤预测制图效果并不完全取决于方法的精密性和复杂性。更本质的原因，应从土壤变异性被制图方法揭示的程度探究。这可能涉及本底数据的详细性（如土壤类型）、关键协变量的应用、方法对关键变量的利用效率等多种因素。本文以南阳市1m土体土壤有机碳密度制图为例，拟通过对土壤类型连接法、普通线性回归、空间地理回归、随机森林、普通克里格、回归克里格等的系统对比，分析土壤变异解释机制对制图效果的影响。

1 材料与方法

1.1 研究区概况

研究区位于河南省西南部（图1），面积2.66万 km2，北亚热带气候，年降雨量800 mm；西北部为中山、低山，东部为低山丘陵，中南部为河流冲积平原，东南续接桐柏山地。按发生分类体系，土壤可分为10个土类（图2a）、19个亚类、37个土属。

1.2 土壤数据源

收集第二次土壤普查时期土壤剖面数据488个，随机抽取其中90%，即439个样点为训练练据进行1m土体SOCD制图，其余49个剖面作为验证数据（图1）。土壤剖面样点记录了特征土层深度区间、每层的土壤有机质、容重、砾石含量和砂姜含量等数据，按下式计算SOCD［3-7］，

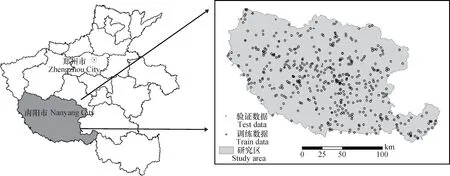
图1 研究区及土壤样点分布图Fig. 1 Distribution of the study area and soil samples

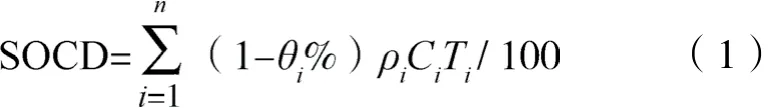
式中，SOCD为土壤剖面有机碳密度（kg m-2）；θi为第i层＞2 mm砾石（砂姜作为砾石对待）含量（%）；ρi为第i层土壤容重（g cm-3）；Ci为第i层土壤有机碳含量（g kg-1），由有机质含量×0.58换算得到；Ti为第i层土层的厚度（cm）；n为参与计算的土壤层次总数；100为用于单位换算的常数。训练数据在土壤表层的有机质（organic matter，OM）含量和1m土体的SOCD统计见表1。

表1 1m土体土壤有机碳密度和表层土壤有机质的统计特征Table 1 Statistical features of SOCD（soil organic carbon density ）of 1 m thickness soil body and OM content of topsoil

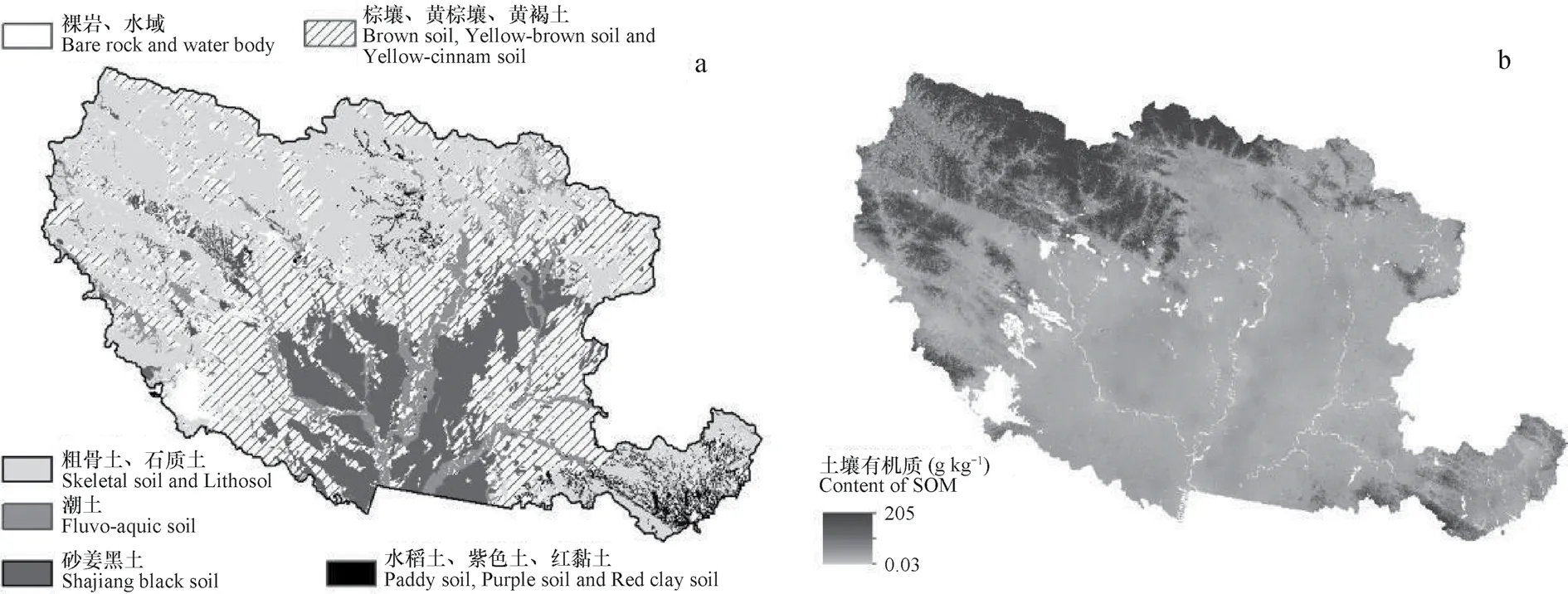
图2 南阳市土壤类型（a）和土壤表层有机质含量（b）示意图Fig. 2 Soil map（a）and topsoil OM content map（b）of Nanyang City

1.3 预测变量选择

地形变量：收集该区30 m分辨率数字高程，取高程、坡度、坡向、平面曲率、剖面曲率、复合地形指数作为预测土壤有机碳的地形变量。

土壤表层有机质数据：土壤剖面最上部土层的有机质含量数据结构性变异比例为67.5%，将其Kriging插值图（图2b）作为预测土壤1m 土体SOCD的变量之一。

遥感数据：南阳市第二次土壤普查工作主要在1980—1983年间开展，各县并不一致，遥感影像年份无法做到与土壤样本采集时间的完全对应。因此，遥感影像数据的应用定位为对土壤母质、土壤相对湿度、山区自然植被差异等信息的补充，上述信息受人为土地利用干扰相对较少，可放宽对遥感时效的要求。特在可得数据源中选择了1990年5月2日云量为0%的TM影像（通过地理空间数据云平台下载），当地主要农作物——小麦此时已成熟，影像数据更利于反映自然植被类型差异和土壤差异。提取TM1-7波段、归一化植被指数、穗帽变换（Tasseled cap transformation，TC）的3个成分亮度、绿度、湿度（Wetness of TC，TCW）等作为土壤有机碳密度制图的环境协变量。

1.4 土壤类型连接法

基于南阳市1∶5万数字化土壤图，按土属、亚类、土类3个分类级别进行概括，依次得到土属图、亚类图和土类图；分别采用均值连接法（Mean法）、中值连接法（Median法）将土壤剖面计算得到的碳密度值连接到土壤图图斑。

1.5 模型法

WLS回归：即加权最小二乘法线性回归。在普通最小二乘法回归（OLS）公式Y=XB+μ基础上（其中Y为因变量，X为自变量，B为回归系数，μ为随机误差），构建权重矩阵W=DDT，使D-1Y=D-1XB+D-1μ，按 ˆB=（XTW-1X）-1XTW-1Y计算回归系数，即为WLS回归。WLS回归改变了OLS回归中所有变量贡献相同的假设，而使变异较大的观察值对分析的影响小、变异小的观察值对分析的影响大，可取得更理想的回归模型。本研究采用变量乘幂的导数为权重值，幂值在SPSS中根据最大似然法估计λ的最优值。得到WLS方程后，在ArcGIS10.3中进行计算，实现SOCD的预测。

GWR回归：即地理权重最小二乘法回归［10，28］。其公式为其中（μi，νi）表示第i个采样点坐标，βj（μi，νi）为第i个采样点的第j个自变量xij的回归系数，εi为该点的回归误差。GWR回归中，周围采样点根据其距离预测点i的距离计算其进入回归方程时的权重，每个采样点相对于其他采样点均有一个权重系数，n个采样点就构成n×n空间权重对角矩阵，本文采用二次距离衰减函数拟合权重系数，公式为wij=［1-（dij/h）2］2∣dij＜h，wij=0∣dij＞h，其中dij为两点间的欧氏距离，h为衰减函数的带宽，超出h认为样点的作用权重为0。带宽的确定一般有固定内核和自适应内核两种方法，前者给出确定性带宽，后者则根据样点密度分布进行自动调整，本文采用自适应内核。通过计算wij构造权重矩阵W（μi，νi），进而估算回归系数 ˆB=（XTW（μi，νi）X）-1XTW（μi，νi）Y。应用ArcGIS 10.3地理回归工具模块进行计算。

随机森林（Random Forest，简写为RF）：由Breiman［29］改进分类树算法而来，是一种机器学习算法。其优点是：可以避免过拟合、能同时利用名义变量（如土壤类型）和数值变量；每次运行随机森林，均随机抽取1/3的数据不参与建模，被称为范围外数据（Out of Bag，简称OOB），模型自动对OOB数据实测值和模型运算值交叉检验，计算OOB数据变异的解释比例，是对整个训练数据变异解释比的无偏估计。

1.6 验证方法

根据验证数据集验证和训练数据集交叉验证的相关系数（r）、平均预测误差（ME）、均方根预测误差（RMSE）、变异解释比（Varex）对SOCD预测结果进行评判［11-12］。其中

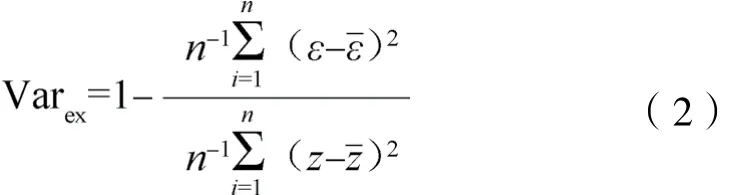
式中，ε为预测误差，为预测误差均值，z为实测有机碳储量，为实测有机碳储量均值。

2 结果与讨论

2.1 土壤SOCD的变异解释与关键参数特征

随机森林的范围外数据分析可提供SOCD关键协变量解释力无偏估算途径，当训练树足够多时，结果具有高度的重复性（表2）。由表2可知：第1，土属对SOCD变异的解释能力最强，其次是亚类、土类、有机质，3次随机计算的平均解释力分别达到40.8%、37.9%、37.0%和21.9%。第2，土属与土壤OM组合达到了57.5%的变异解释比，附加其他变量过多又导致变异解释比降低，所有变量全部应用仅达到52.7%的变异解释比。第3，排除土壤OM和土壤类型信息，其他变量对SOCD变异的综合解释能力不超过2%。第4，高程、坡度和湿度指数（TCW）等单独使用对SOCD变异的解释力为负，即完全没有规律性，但与一些重要变量结合，则提高原有变量的解释力，如OM+TCW解释力上升为28.9%。上述结果定量说明：（1）在预测SOCD方面土壤类别是最重要的变量，其次是土壤表层OM。（2）所有变量共同参与建模并不能达到最高的解释力，可见非重要变量进入模型增加了噪声。（3）高程、坡度、TCW等的作用效果是依附主要变量的，即主要参与对主要变量预测结果进一步细分，可以认为它们只解释局部的数据变异性。

纯空间方法不需借助协变量，而是从空间相关性的角度对土壤SOCD变异性进行解释。尽管SOCD空间相关性与其关键协变量在空间上的变化规律可能有关，但就数学原理而言，它们提供了完全不同的解释机制。变异函数分析表明，SOCD在14 400 m变程范围内具有40.5%的空间变异结构性（图3a），即可由空间相关性解释的总方差为40.5%，这一数值低于关键参数组合所能达到的最大变异解释力，而与土壤类型对SOCD变异的解释力接近。

回归Kriging模型对土壤SOCD变异的解释可分为趋势模型和残差变异函数特征两个部分。很显然，趋势和残差不是互相独立的，不同方法提取趋势值后残差的空间变异结构性显著不同。以土壤类型均值、中值提取趋势值后的的SOCD残差呈现较强的随机变异特征，理论上不能再借助空间相关性途径获得补充性的变异解释；采用土壤类型和土壤表层OM等关键变量组合进行随机森林建模计算的结果残差亦如此；而WLS、GWL和RF（OM+TCW）方法提取趋势后的残差空间变异结构性达到33.1%、25.0%和25.9%，残差可提供额外的变异解释。

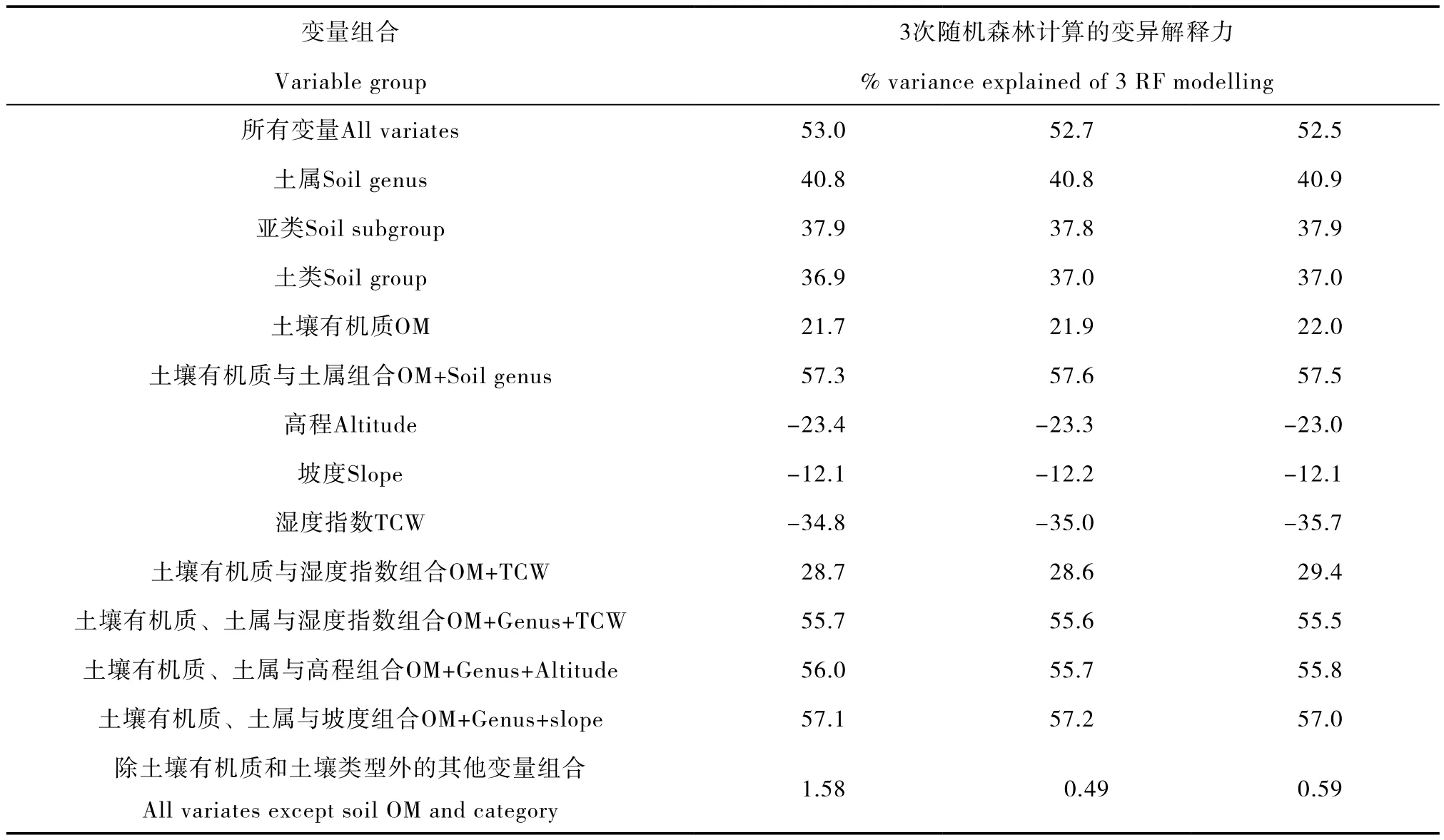
表2 基于随机森林的预测变量对SOCD变异的解释力Table 2 Variance explanation of covariates for predicting SOCD of 1m thickness soil body based on RF model

2.2 土壤类型连接法制图

土类、亚类、土属的Mean连接法结果见图3。土类图、亚类图、土属图斑数分别为2 213、2 866、4 057，从亚类～土属的图斑详细度增加较大，制图细节的变化也主要发生在亚类～土属的变化。验证数据集参数的改善也主要体现这一特征（表3）：其数据集验证的r分别为0.51、0.51和0.58，Varex为0.29、0.30和0.35。ME为-0.41、-0.43、-0.31；Median连接法具有类似规律，但验证集中Median法的r值和Varex普遍略低于同分类级别的Mean法的r值和Varex，说明对土壤类型估值而言，本例中均值较中值可能更有代表性。土壤类型连接法的突出特征还表现在图斑边界线两侧的突变明显，空间变异的渐变性表现不佳。

图3 基于土壤类型连接法的SOCD制图Fig. 3 SOCD maps based on soil category linkage method

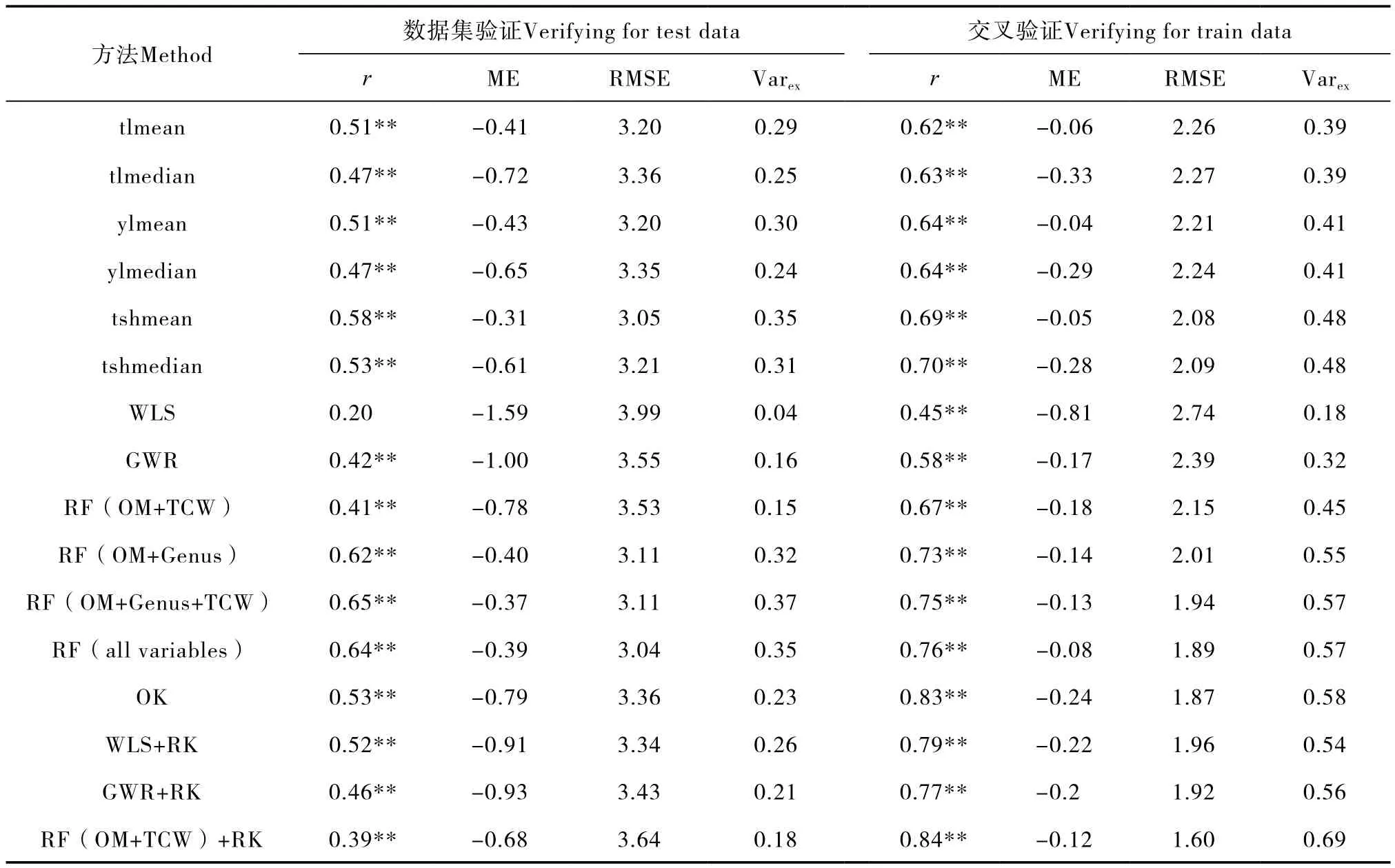
表3 有机碳密度制图的结果验证Table 3 Verification of the SOCD maps

2.3 回归模型法制图

用逐步回归筛选出土壤表层OM和TCW构成对SOCD的最佳解释变量组合，其他变量则由于多重共线性而被排除。WLS回归系数r为0.45，关系式为

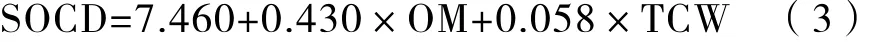
WLS回归预测的SOCD表现明显的平滑效应，且出现最小值为负的极端推论（图4a）。其验证数据集r系数为0.20（表3），Varex为0.04，实际预测效果明显不如土壤类型连接法。

同样采用OM和TCW变量进行SOCD的GWR回归，制图效果较WLS回归平滑效应小、局部细节变异获得较好拟合（图4b），验证数据的r为0.42，Varex为0.16，较WLS回归明显改善（表3）。从制图形式上GWR结果更接近土壤类型连接法，但对验证数据集的预测效果仍不如后者。

图4 基于WLS（a）和GWR（b）的SOCD制图Fig. 4 SOCD maps based on WLS regression（a）and GWR regression（b）

2.4 随机森林法制图

基于O M和T C W的随机森林制图，即R F（OM+TCW）结果见图5a，其验证数据的r为0.41，Varex为0.15，精度与GWR法相当。

OM+Genus（土属）、 OM+Genus+TCW（图5b）、“所有变量”等3种组合方式下的RF预测结果相似，文中只列出一种。比较可知，较之土壤类型法和其他模型法，结合了土壤类型和土壤OM的RF结果既避免了土壤图斑边界两侧的突变，也较大程度避免了平滑效应、突出了空间变异的细节，并防止了WLS和GWR的过度外推。其验证数据集的r分别达到0.62、0.65、0.65，Varex为0.32、0.37、0.35，检验指标优于土壤类型连接法、GWR回归和WLS回归。

2.5 普通克里格和回归克里格的制图

对土壤有机碳密度进行普通Krging插值的结果（图6a）在宏观趋势方面与土壤类型法、RF（OM+Genus+TCW）均较接近，但在细节表达方面稍欠佳。表现为验证数据检验的r为0.53，与土壤类型连接法相当，而Varex为0.23，略低于后者。然而，在趋势和细节表达方面，普通Kriging结果均较WLS和GWR结果好。

土壤类型连接法、随机森林法、GWR法的交叉验证结果均显示（表3），它们的制图结果与训练数据的拟合程度较好，因此它们的残差呈随机性变异的可能性更大。此外，不同的趋势提取方法也影响到残差的计算，最终的变异函数计算表明：仅对WLS、GWR和RF（OM+TCW）的计算结果执行残差Kriging具有实际意义。数据集检验的结果显示：尽管WLS原始结果表现最差，但通过残差Kriging其预测效果得到的补偿最为显著，最终WLS+RK的效果优于GWR+RK，而RF（OM+TCW）+RK的效果最差（表3）。

图5 基于随机森林的SOCD制图Fig. 5 SOCD maps based on RF models

图6 基于普通Kriging（a）和回归Kriging的SOCD制图（b：WLS回归+残差Kriging）Fig. 6 SOCD maps based on ordinary kriging（a）and regression kriging（b：WLS regression+residual kriging ）

与普通Kriging类似，WLS+RK在趋势方面与土壤类型Mean连接法和RF（OM+Genus+TCW）的结果很相似（图6b），但在细节方面略逊，表现为验证数据集的r和Varex略低。尽管以残差Kriging进行了补偿，GWR+RK、RF（OM+TCW）+RK的效果未达到普通Kriging和土壤类型连接法的同等效果。必须指出，较之土壤类型连接法和其他模型法，回归Kriging使训练数据交叉检验的参数r、RMSE和Varex均显著改善，这显然是由于在训练点位置残差得到补偿的结果，制图效果和验证数据集的检验均表明这种改善的“预测意义”不大。

3 结 论

制图效果取决于制图模型是否充分利用了训练数据中关键预测变量、空间变异函数或者它们的组合所蕴含的解释力，方法复杂性的影响则在其次。在南阳地区，土壤表层有机质含量对1m土体SOCD变异的解释力为21.9%；土类、亚类、土属所能解释的1m土体SOCD变异为37.0%～40.8%；土属与土壤表层OM对SOCD变异的联合解释能力为57.5%；变异函数提供的空间相关性对SOCD变异的解释力为40.5%。各类SOCD制图方法的效果与其所用参数的解释力关系密切：同时利用土壤类型和土壤表层OM的随机森林RF（OM+Genus）或RF（OM+Genus+TCW）等效果较好；土壤类型连接法、普通Kriging插值的效果次之；GWR和RF（OM+TCW）采用非线性回归方式进行建模的效果明显优于WLS，但由于仅利用到关键参数OM，它们的总体效果显著低于前述方法。空间相关性与关键协变量建模是两种不同的解释机制，它们所能解释的土壤变异可能包含或交叉重叠，并不能保证回归Kriging是最优方法，本例中WLS、GWR和RF（OM+TCW）得到残差补偿后并没有使其制图效果达到RF（OM+Genus）或RF（OM+Genus+TCW）的精度水平。并且趋势性建模方式也不可避免影响到残差变异结构的计算：WLS、GWR和RF（OM+TCW）在原始模型中对训练数据的拟合效果依次升高，但其RK结果的优劣排序则相反。

［1］ Bohn H L. Estimate of organic carbon in world soils.Soil Science Society of America Journal，1982，46：1118—1119

［2］ Batjes N H. Total carbon and nitrogen in the soils of the world. European Journal of Soil Science，1996，47（2）：151—163

［3］ 解宪丽，孙波，周慧珍，等. 中国土壤有机碳密度和储量的估算与空间分布分析. 土壤学报，2004，41（1）：35—43 Xie X L，Sun B，Zhou H Z，et al. Organic carbon density and storage in soils of China and spatial analysis（In Chinese）. Acta Pedologica Sinica，2004，41（1）：35—43

［4］ Shi X Z，Yu D S，Warner E D，et al. Soil database of 1∶1 000 000 digital soil survey and reference system of the Chinese genetic soil classification system. Soil Survey Horizon，2004，45（4）：129—136

［5］ 于东升，史学正，孙维侠，等. 基于1∶100 万土壤数据库的中国SOCD及储量研究. 应用生态学报，2005，16（12）：2279—2283 Yu D S，Shi X Z，Sun W X，et al. Estimation of China soil organic carbon and density based on 1∶1000 000 soil database（In Chinese）. Chinese Journal of Applied Ecology，2005，16（12）：2279—2283

［6］ 张勇，史学正，于东升，等. 属性数据与空间数据连接对土壤有机碳储量估算的影响. 地球科学进展，2008，23（8）：840—847 Zhang Y，Shi X Z，Yu D S，et al. Effects of the linkage between spatial data and attribute data on estimates of soil organic carbon（In Chinese）. Advances in Earth Science，2008，23（8）：840—847

［7］ 支俊俊，荆长伟，张操，等. 利用1∶5 万土壤数据库估算浙江省土壤有机碳密度及储量. 应用生态学报，2013，24（3）：683—689 Zhi J J，Jing C W，Zhang C，et al. Estimation of soil organic carbon density and storage in Zhejiang Province by using 1∶50 000 soil database（In Chinese）.Chinese Journal of Applied Ecology，2013，24（3）：683—689

［8］ Minasy B，Mcbratney A B，Malone B，et al. Digital mapping of soil carbon. Advances in Agronomy，2013，118（118）：1—47

［9］ Ratnayake R R，Karunaratne S B，Lessels J S，et al.Digital soil mapping of organic carbon concentration in paddy growing soils of Northern Sri Lanka. Geoderma Regional，2016，7（2）：167—176

［10］ 王库. 基于地理权重回归模型的土壤有机质空间预测.土壤通报，2013，44（1）：21—28 Wang K. Spatial estimation of soil organic matter by using geographically weighted regression model（In Chinese）. Journal of Chinese Journal of Soil Sciecne，2013，44（1）：21—28

［11］ Wiesmeier M，Barthold F，Blank B，et al. Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem. Plant Soil，2011，340（1）：7—24

［12］ 王茵茵，齐雁冰，陈洋，等. 基于多分辨率遥感数据与随机森林算法的土壤有机质预测研究. 土壤学报，2016，53（2）：342—354 Wang Y Y，Qi Y B，Chen Y，et al. Prediction of soil organic matter based on multi-resolution remote sensing data and random forest algorithm（In Chinese）. Acta Pedologica Sinica，2016，53（2）：342—354

［13］ Mansuy N，Thiffault E，Paré D，et al. Digital mapping of soil properties in Canadian managed forests at 250 m of resolution using the k-nearest neighbor method. Geoderma，2014，235/236（4）：59—73

［14］ Tiwari S K，Saha S K，Kumar S. Prediction modeling and mapping of soil carbon content using artificial neural network，hyperspectral satellite data and field spectroscopy. Advances in Remote Sensing，2015，4（1）：63—72

［15］ Martin M P，Orton T G，Lacarce E. Evaluation of modelling approaches for predicting the spatial distribution of soil organic carbon stocks at the national scale. Geoderma，2014，223/225：97—107

［16］ Sandeep K. Estimating spatial distribution of soil organic carbon for the Midwestern United States using historical database. Chemosphere，2015，127：49—57

［17］ Doetterl S，Stevens A，van Oost K，et al. Spatiallyexplicit regional-scale prediction of soil organic carbon stocks in cropland using environmental variables and mixed model approaches. Geoderma，2013，204/205（4）：31—42

［18］ Somarathna P D S N，Malone B P，Minasny B. Mapping soil organic carbon content over New South Wales，Australia using local regression kriging. Geoderma Regional，2016，7（1）：38—48

［19］ Guo P T，Li M F，Luo W，et al. Digital mapping of soil organic matter for rubber plantation at regional scale：An application of random forest plus residuals kriging approach. Geoderma，2015，237/238：49—59

［20］ Ungaro F，Staffilanii F，Tarocco P. Assessing and mapping topsoil organic carbon stock at regional scale：A scorpan kriging approach conditional on soil map delineations and land use. Land Degradation &Development，2010，21（6）：565—581

［21］ Taghizadeh-Mehrjardi R，Nabiollahi K，Kerry R.Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh region，Iran. Geoderma，2016，266：98—110

［22］ Miller B A，Koszinski S，Hierold W，et al. Towards mapping soil carbon landscapes：Issues of sampling scale and transferability. Soil & Tillage Research，2015，156：194—208

［23］ 顾成军，史学正，于东升，等. 省域土壤有机碳空间分布的主控因子-土壤类型与土地利用比较. 土壤学报，2013，50（3）：425—432 Gu C J，Shi X Z，Yu D S，et al. Main contributing SOC spatial distribution at the province scale as affected by soil type and land use（In Chinese）. Acta Pedologica Sinica，2013，50（3）：425—432

［24］ 郭治兴，袁宇志，郭颖，等. 基于地形因子的土壤有机碳最优模型. 土壤学报，2017，54（2）：331—343 Guo Z X，Yuan Y Z，Guo Y，et al. Optimal estimation model of soil organic carbon based on the terrain factor（In Chinese）. Acta Pedologica Sinica，2017，54（2）：331—343

［25］ Brungard C W，Boettinger J L，Duniway M. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma，2015，239/240：68—83

［26］ Heung B，Chak Ho H，Zhang J，et al. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping.Geoderma，2016，265：62—77

［27］ Taghizadeh-Mehrjardi R，Nabiollahi K，Minasny B，et al. Comparing data mining classifiers to predict spatial distribution of USDA-family soil groups in Baneh region，Iran. Geoderma，2015，253/254：67—77

［28］ Fotheringham A S，Brunsdon C，Charlton M E.Geographically weighted regression. England：John Wiley and Sons，LTD. Sussex. 2002：27—64

［29］ Breiman L. Random forest. Machine Learning，2001，45：5—32