基于Romax Designer的圆锥滚子轴承载荷分析

洛阳轴承研究所有限公司 铁晓艳 张振潮 王虎强 郑志功

1 引言

圆锥滚子轴承可以承受径向和轴向的联合负荷，广泛应用于汽车车轮、轴箱及减速器等关键部位的回转机械，是决定整个系统性能的关键元件之一，因此对其可靠性有着严格要求。

众所周知，影响滚动轴承疲劳寿命的主要因素即滚子与内外圈的接触应力变化规律和最大应力值，而其最大应力和应力变化规律不仅与轴承的结构和几何尺寸有关，还与滚子所承受的载荷大小和载荷分布有关。因此，研究圆锥滚子轴承的载荷分布，确定受载最大的滚动体所受的最大载荷和最大应力值，对于分析圆锥滚子轴承的内部载荷分布与接触应力，从而提高轴承的疲劳寿命具有一定的指导意义[1]。

2 研究对象及工况

根据圆锥滚子轴承既可以承受径向载荷，也可以承受轴向载荷的特性，本文以施加联合载荷（同时施加径向载荷和轴向载荷）来研究分析圆锥滚子轴承的内部载荷分布，如最大法向载荷、最大接触应力、最大变形量。

选取某客户汽车用圆锥滚子轴承30311为分析对象，根据用户工况条件的要求，已知轴承工作温度为60～80℃，转速为2000r/min，同时施加径向载荷Fr=45000N和轴向载荷的联合载荷。如表1所示为30311圆锥滚子轴承结构参数[2]。其中，

又知：

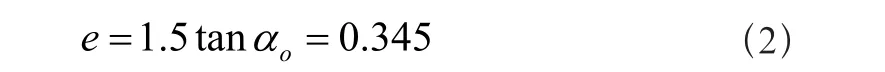
比较式（1）、（2）可知（1）＞（2），则径向动载荷系数X=0.4，轴向动载荷系数当量动载荷为：

表1圆锥滚子轴承30311结构参数

3 联合载荷下30311轴承理论计算

对于满足弹性接触赫兹理论的线接触的滚动轴承，在进行圆锥滚子轴承内部载荷计算时，通常将圆锥滚子轴承外圈与滚子的接触角oα当作轴承公称接触角[2]，因此有判别式：

通过Sjoväs积分表[2]，可得径向载荷积分Jr(ε)=0.2225，载荷分布系数ε= 1.1675，因ε＞1，则所有滚子均受载。值得指出的是，此处假设所有受力中的滚子接触角是不变的，则滚子与外滚道间最大法向接触载荷为：

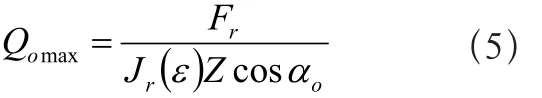
如图1所示为30311圆锥滚子轴承单个滚子的受力平衡示意图，其中，滚子与内、外滚道和挡边的接触载荷分别为Qi、Qo和Qf，它们的接触角分别为αi、αo、αf。当滚子平衡时，各接触载荷满足下列平衡方程[3]：

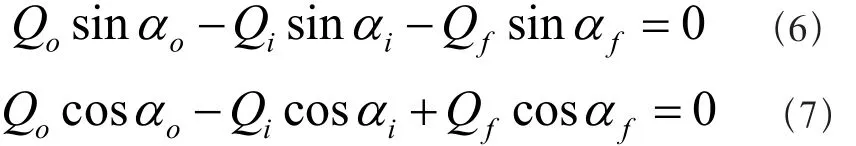
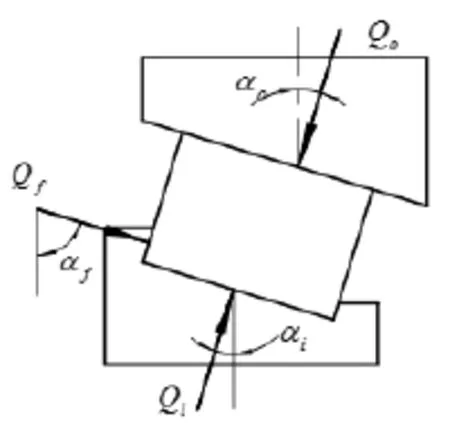
图1 圆锥滚子轴承力平衡示意图

以外滚道接触载荷Qomax为接触变量，可求得滚子与内滚道间最大法向接触载荷为：

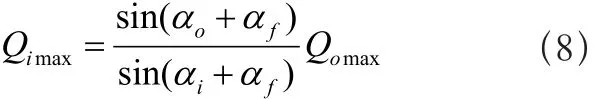
滚子与挡边间最大法向接触载荷为：

任意角度位置ϕ处，滚子与滚道间法向接触载荷为[2]：

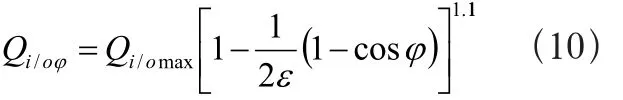
计算可得轴承内部载荷分布如图所示，各处数据值如表2所示。图中0°方位角为轴承安装后最下端位置，即受载最大位置。

图2 内部载荷分布示意图

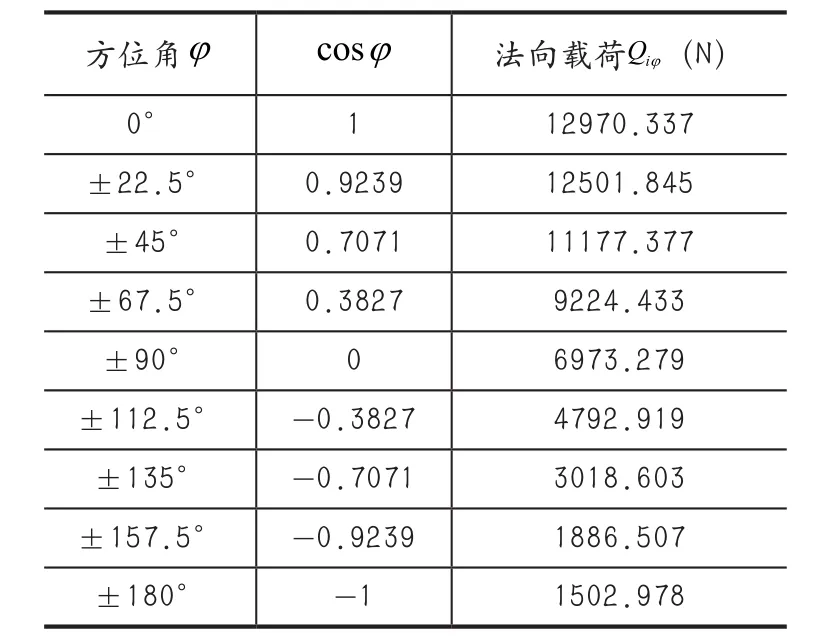
表2 联合载荷时轴承内部载荷分布

已知内、外滚道接触处的曲率和[3]为

理想线接触时，内、外滚道接触面半宽最长[3]为：

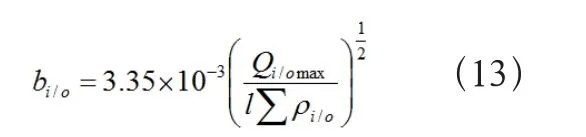
则内、外滚道最大法向接触应力为：

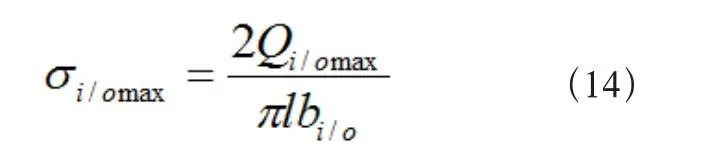
根据Palmgren公式，内、外滚道最大接触变形为：

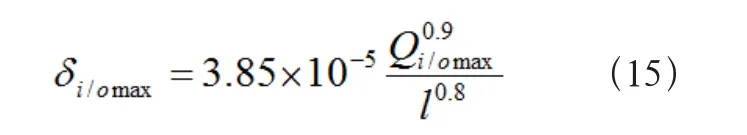
经计算，可得施加联合载荷时，圆锥滚子轴承载荷与应力理论计算结果如表3所示。

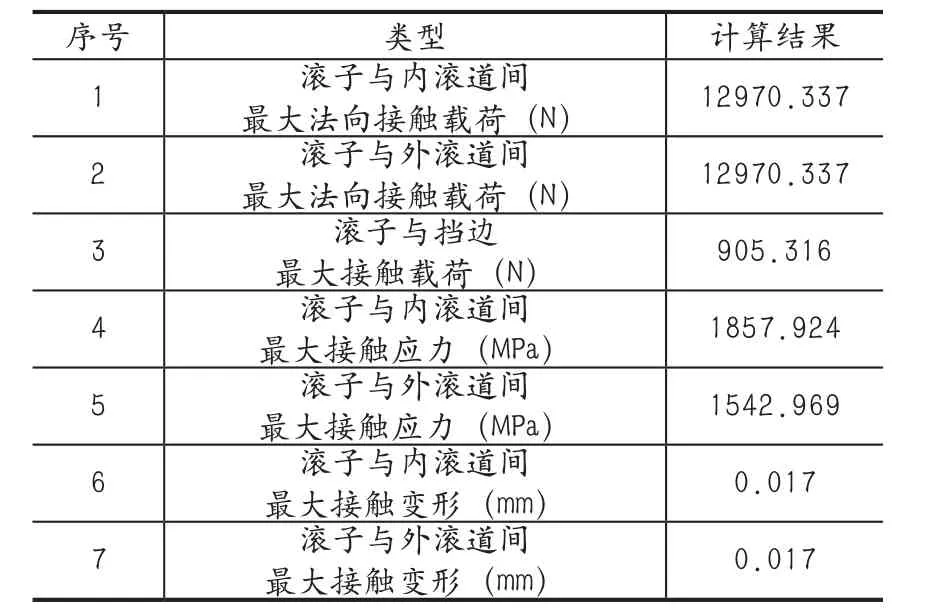
表3 联合载荷时轴承内部载荷分布

由以上结果可以看出，滚子与内、外滚道间的最大法向接触载荷相等，滚子与内、外滚道间任意位置处的法向接触载荷也相等，滚子与内、外滚道间的最大接触变形亦相等。

4 基于Romax Designer的30311轴承载荷分析

4.1 Romax Designer软件介绍

RomaxDesigner是英国Romax科技有限公司开发的工程设计仿真分析软件，主要应用于传动系统领域的齿轮传动系统虚拟样机的设计和分析，在全球传动系统设计领域享有盛誉，目前已成为汽车、风电及齿轮传动应用领域认可且受到广泛使用的分析软件。

软件采用系统建模与分析的思想计算传动系统变形及各部件上的载荷状况，同时考虑系统中各部件之间的相互作用和影响，能够对系统中的齿轮强度、接触应力、轴承寿命、轴疲劳进行计算。将轴承在轴系中的功能与作用充分发挥，使轴承内部载荷分布更贴近实际工况条件[4]。

4.2 Romax Designer建模与分析结果解析

如图3所示为圆锥滚子轴承30311实际工作时的轴系结构图。应用RomaxDesigner的轴系建模模块，建立该轴系系统模型[5]，同时，对轴承施加上述联合载荷，即径向载荷如图4所示。

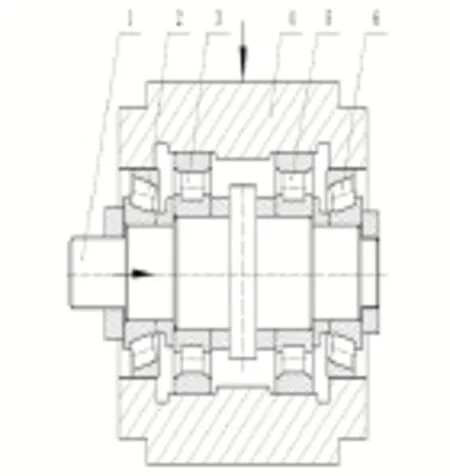
图3 圆锥滚子轴承联合载荷试验装配简图

图4 Romax Designer环境下模型图

在RomaxDesigner环境下建模时的几点说明如下：轴系和外套均为刚性体；采用一对背对背安装的30311圆锥滚子轴承（具体几何参数见表1）作为分析对象，同时选用两组NUP313E型号的圆柱滚子轴承（选用SKF公司轴承）作为支承轴承；轴左端添加输入功率载荷，省略输出功率载荷；径向载荷添加位置位于两套背对背安装的30311轴承的对称中心处，方向向下。轴向载荷从轴的左端指向右端方向。

运行轴承分析后的结果如图5、6、7、8所示。

图5 滚子与内、外滚道间载荷雷达图

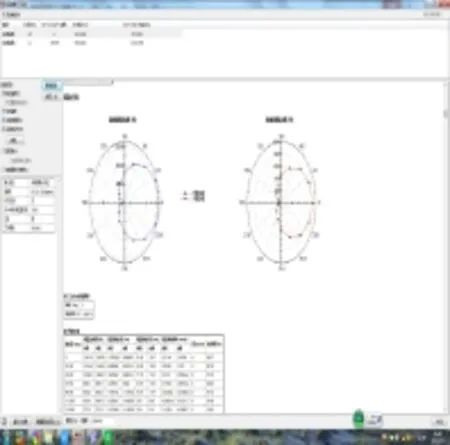
图6 滚子与挡边间载荷雷达图

其中，图5为滚子与内、外滚道间的载荷雷达图，由图可知，内、外滚道接触载荷线重合（相等），且与图2进行理论计算时的示意图规律相同。根据公式（9）可知滚子与挡边间的载荷分布与滚子与外滚道载荷分布相同，故图6所示的滚子与挡边间载荷雷达图反映了理论计算的准确性。

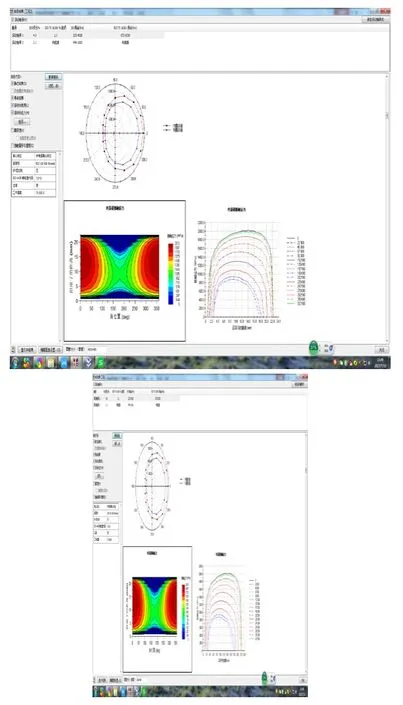
图7 滚子与内、外滚道间最大接触应力雷达图

图8 内滚道接触应力平铺图

图9 外滚道接触应力平铺图

如图7所示谓滚子与内、外滚道间最大接触应力雷达图，由图可知内圈最大接触应力大于外圈所受最大接触应力，但两者分布规律相同。图8、图9分别为滚子与内、外滚道接触应力的平铺展开图。由图可知，在0°和360°位置处的接触应力最大，且在滚子长度方向上呈现出应力分布趋势。

5 结论

通过本文的理论计算与软件仿真计算，圆锥滚子轴承联合载荷作用下，全部滚子受载，且受载遵循沿圆周方向向两边扩散的规律。如表4所示为理论计算与仿真分析结果的对比，可知误差均小于15%。从而进一步证明了运用Romaxdesignher软件进行圆锥滚子轴承联合载荷的仿真分析可以在一定程度上反应真实的工况情况，具有借鉴性。