在小学相遇问题中培养学生的抽象思维能力

江苏省江阴市南闸中心小学 居新霞

在小学数学教学中，教师必须一边引导学生学习知识，一边培养学生的抽象思维水平。小学生只有具备了抽象思维的能力，才能够理解每个数学问题背后的核心本质。然后教师要如何培养学生的抽象思维能力呢？这是一些数学教师的困惑。现应用小学数学相遇问题的教学为例，说明培养学生抽象思维能力的方法。

一、引导学生提炼具象文本中的抽象信息

小学生的思维能力特点是具象化思维能力较强，他们容易沉浸在具象化的情境中、具象化的案例中，而不能从抽象的角度来理解具象化问题背后的本质。教师如果要培养学生的抽象思维能力，就要引导学生把抽象的本质与具象化的情境剥离开来，能用抽象思维来思考问题。

比如以教师引导学生思考以下的问题为例：快车和慢车同时从相距357千米的两地出发，相向而行，经过3小时后快车与慢车相遇，快车的速度是95千米/时，则慢车的速度是多少？很多学生看到这个问题之后，把探索的信息放在快车是什么、慢车是什么？然后他们能够不断地发散联想，把学习时间和精力投入到还原具象化的情境中。为了帮助学生建立抽象思维，教师要引导学生分析：第一，在文本中具有数量关系的事物是什么？第二，在文本中影响数量关系的关键词是什么。经过教师的引导，学生会发现具有数量关系的事物是快车和慢车的行驶时间、快车和慢车的行驶速度、快车和慢车的行驶距离。影响数量关系的关键词是两地出发、相距、相遇、相向而行。文本中其他的信息与数量关系无关，于是不用花费精力思考。

教师在引导学生学习数学知识时，要引导学生学会抽取抽象的数量信息，这是学生学会应用抽象的视角分析数学问题的基础。

二、引导学生分析具象图形中的抽象关系

小学生的抽象思维能力还比较弱，他们不能在提取了文本中的抽象信息后，直接建立数学关系。为了让学生能够从具象化的数学问题抽取抽象化的数学关系，教师要引导学生学会根据抽象信息来绘制数学图像，然后从数学图像中提取抽象的数量关系。

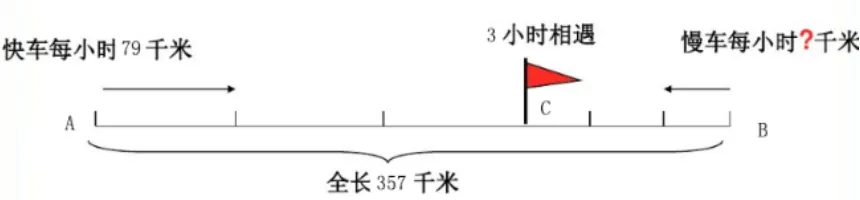
比如，当学生提取了文本中的数量关系以后，教师要引导学生画标准的、规范的线段图。教师可让学生了解，现在快车和慢车相距是540千米，可以应用一条直线来描述这段距离；快车的起点设为A，慢车的起点设为B；根据文本的信息，快车和慢车都走了三个小时并相遇，那么现设相遇的地点为小旗所插之处，也可设为C；C的左侧是快车行驶的距离、右侧是慢车行驶，然后以快车和慢车相遇的时间，绘制单位时间的刻度，标注单位时间中快车及慢车的行驶速度。以上图形中，如已有数量信息，则标注数量信息，如无数量信息，则设元为x。小学生通过观看这样的图形，则立即理解了数学问题的数量关系：全长=快车行驶的距离+慢车行驶的距离，快车行驶的距离为时间×速度，慢车行驶的距离为时间×速度。根据数量关系可列方程，建立等量关系为357=3×79+3x，357=237+3x，3x=120，x=40。通过这一次的学习，学生意识到了当遇到相遇问题，不能建立数量关系时，可以把抽取到的数量关系绘制到图形上，结合图形来分析数量关系。

小学生的抽象思维能力不足，有时他们很难从抽象的层面来思考抽象的信息，为了帮助学生思维，教师在教学中要培养学生的数形思想。教师要引导学生学会把抽象的数量信息绘制在图形上，然后结合图形的信息来发现抽象的数学关系。通过这样的训练，学生会了解当抽象思维能力不足时，要如何应用具象化的图形来分析抽象的数学关系，然后建立抽象的数学关系公式。

三、引导学生理解具体案例中的抽象规律

当学生学会了分析数学文本中的抽象信息，能够建立抽象数学关系以后，教师要引导学生发现数学案例中的规律，然后根据具象化的案例中呈现出来的规律来归纳总结抽象的问题规律，这些规律可以成为学生解决这类问题的理论指导。

比如教师可引导学生分析以下的习题：小明和小华骑着电动车从相距190千米的两地出发，相向而行。小明的行驶速度是36千米/时，小华的速度是40千米/时，两人在几小时后能相遇？教师可引导学生结合刚才学习的结果提取文本中的数学信息，通过绘制线段图建立数学关系。学生经过思考，完成以上的步骤，得到方程：36x+40x=190，76x=190，x=2.5。当学生完成了学习以后，教师引导学生思考。刚才以上所有的问题探讨的都是什么问题？学生经过思考，认为可以把问题归纳为相遇问题。教师引导学生思考，相遇问题涉及的数量关系是什么？学生表示涉及的数量关系为总距离、总速度、总时间；甲走过（或行驶）的距离、甲的速度、甲用的时间；乙走过（或行驶）的距离、甲的速度、甲用的时间。教师引导学生思考，结合以上的案例，可以建立哪些等量关系公式？学生经过思考，得到以下的公式：总距离=总速度×总时间；总距离=甲走过（或行驶）的距离+乙走过（或行驶）的距离；总距离=甲的速度×甲用的时间+乙的速度×乙用的时间；总距离=（甲的速度+乙的速度）×甲、乙相遇用的时间。当学生从具象的案例中抽取了这样的数学公式以后，学生突然有所悟。学生意识到以后再遇到相遇问题时，可以直接套用这套规律来分析文本，建立数量关系；只要深入理解这套规律，他们甚至可以省去绘制线段图的时间。

教师在教学中，要引导学生学会在具象化的案例中，抽取抽象化的数学规律。教师要引导学生发现具象案例中的共通点，在共通点中找规律。教师要让学生意识到，学习数学知识时，不能只是掌握解决具象化数学案例的技巧，学生必须抽取解决某一类数学问题的规律，形成解决这一类数学问题的数学理论指导。只要学生长期受到这样的训练，他们就能够从具象化的案例中抽取抽象化的理论。

总之，教师在教学中要引导学生学会抽取文本中的抽象化的数量信息、从数学图形中分析抽象化的数量关系、在具象化的案例中抽取抽象化的规律。只要学生长期受到这样的训练，就能够逐渐把具象化的情境与抽象化的本质剥离出来，然后学会从抽象化的角度思考问题。