2014年高考浙江卷第21题解法探究

内蒙古呼和浩特市第十四中学高三（15）班 苗雨欣

一、原题呈现

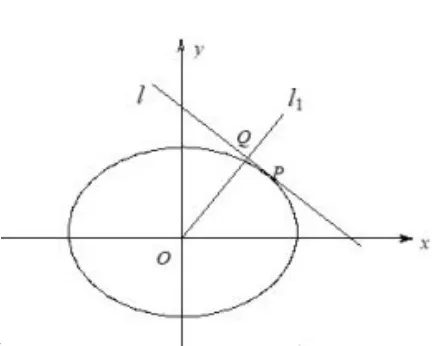
（1）已知直线l的斜率为k，用a，b，k表示点P的坐标；

（2）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a-b。

二、解法探究

思路1：（1）因为直线l的斜率为k，所以切线方程为y=kx±与椭圆方程联立方程组，从而求出P点的坐标；

（2）利用垂直关系求出垂线l1的方程，利用点到直线的距离公式求出点P到直线l1的距离，再利用基本不等式求出距离的最大值。

解法1：（1）已知直线l的斜率为k，则直线l的方程为y=kx+m，椭圆方程为联立消去y，得b2x2+a2(k+m)2-a2b2=0，即

因为直线l是椭圆的切线，所以=0，整理得所以切线l的方程为由于P在第一象限，所以切线l的方程为

（2）证明：由题意知，直线l1的方程为所以点P到直线l1的距离为：

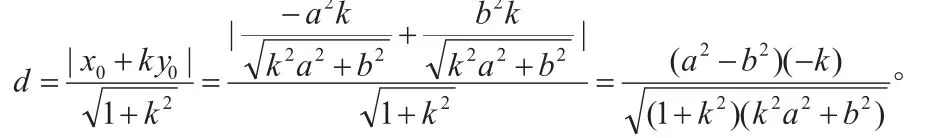
因为点P在第一象限，由①、②联立方程组，解得x0=

所以用a，b，k表示点P的坐标是

（2）证明：直线l1的方程为x+ky=0，则点P到直线l1的距离为

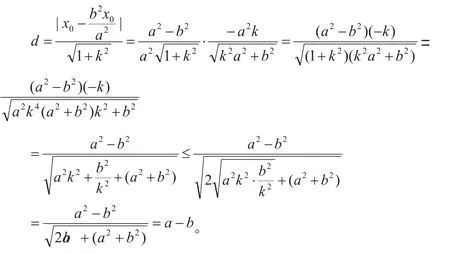
思路3：利用勾股定理

因为点P在第一象限，k＜0，所以可得

所以用a，b，k表示点P的坐标是

（2）证明：设OQ=R，所以点Q在圆上，又在直线l1上，可得④，由③④得：

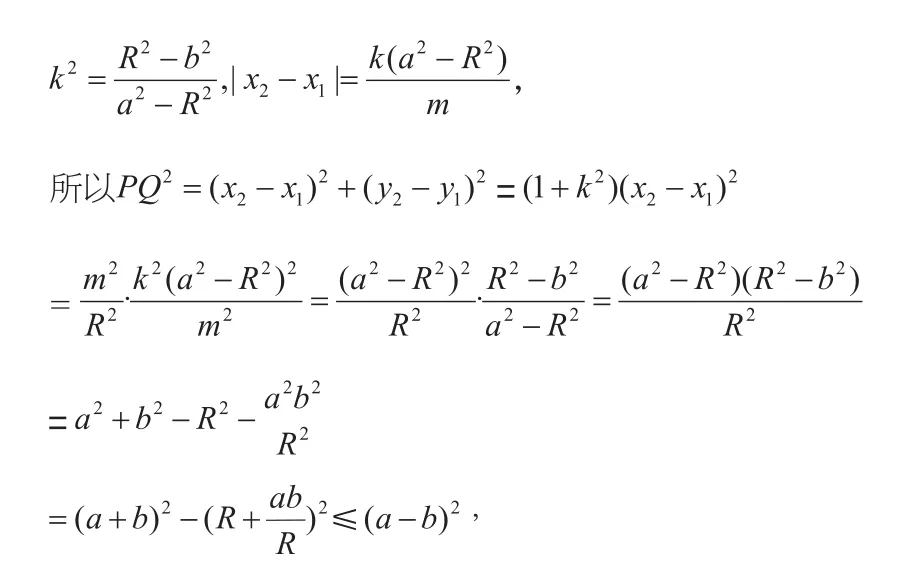
第（2）小问，还可以用法线来简捷证明：

所求点P到直线l1的距离等于坐标原点O到此法线l2的距离d，所以

三、题源追溯

这道浙江高考题是由2004年四川省高中数学联赛一道试题改编而来的：

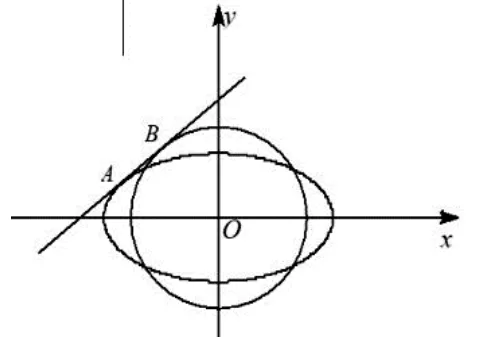
2018年高考江苏卷第18题也是由此竞赛题改编的：如图，在平面直角坐标系xOy中，椭圆C过点焦点圆O的直径为

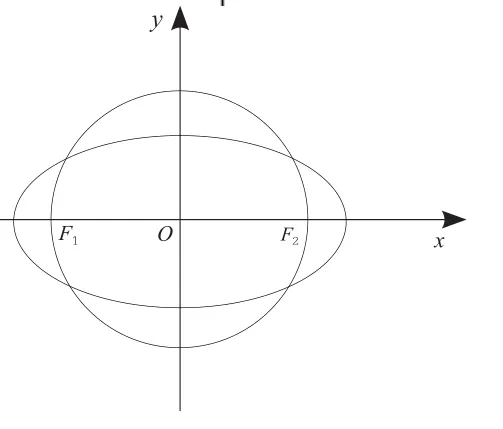
（1）求椭圆C及圆O的方程；

（2）设直线l与圆O相切于第一象限内的一点P。

①若直线l与椭圆C有且只有一个公共点，求点P的坐标；

②直线l与椭圆C交于A、B两点，若△OAB的面积为求直线l的方程。

四、解题启示

这道解析几何题，综合性比较强，有一定的难度，在平时的复习中，要加强综合性问题的训练，让头脑中零散的知识点能够通过解题系统化，同时还要进行专题训练，克服自己的解几何题的畏惧心理，在考试中能迅速找到解题思路。注意一题多解和一题多变，努力提高运算求解能力。