以多元函数最值问题,提升学生数学抽象素养
2018-02-27浙江省绍兴市诸暨市学勉中学楼旭慧
浙江省绍兴市诸暨市学勉中学 楼旭慧
普通高中数学的六个核心素养,是指数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。这些核心素养应贯穿于整个高中数学学习,尤其是对刚进入高中的高一学生而言。
函数是描述客观世界中变量关系和规律的最为基本的数学工具,是贯穿高中数学课程的主线,用函数理解方程和不等式是数学的基本思想方法,在解决实际问题中发挥着重要作用。《普通高中数学课程标准》指出:“用函数理解方程和不等式是数学的基本思想方法,帮助学生用一元二次函数认识一元二次方程和一元二次不等式,理解函数、方程和不等式之间的联系,体会数学的整体性。” 近年来,高考对函数的考查不再是简单的知识叠加型,更侧重于数学核心素养的综合型试题。从历年的各地高考和数学竞赛来看,我们不难发现:对多元函数最值问题的考查趋势逐年有所增加。这显然是为了更好地考查学生的数学抽象和直观想象等数学素养。
其中,数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,获得结论贯穿在数学的产生、发展、应用的过程中。在数学抽象核心素养的形成过程中,学生能更好地理解数学概念、方法和体系,理解和把握事物的数学本质,从而逐渐养成一般性思考问题的习惯,提高数据处理的能力,增强基于数学表达问题的意识。
本文以多元函数的最值问题为例,来谈谈数学抽象核心素养在多元函数最值问题教学中的体现,即体会函数思想在解决方程、不等式问题中的重要作用,帮助学生从函数的角度进一步认识方程和不等式,理解函数、方程和不等式之间的关系,提升数学核心素养。
一、数形结合,必要先行
本题旨在考查学生对函数与不等式联系的理解,对恒成立问题的转化;能力范畴旨在考查学生的数学抽象、直观想象的能力。
本题条件简洁,学生需要对题中所给的条件、数据进行恰当的分析,寻找突破口,探究本质,抽象出一般规律和结构,用数学符号或数学术语予以表征。
由于学生目前的数学抽象能力不强,因而在教学时,我引导学生:“若该题需要你求值f(2),你认为需要知道哪些条件?”学生能快速反应需要知道系数a,b,c三个量或其关系”。此时,学生顿悟本题的关键在于弄清a,b,c三者间的关系以及某元的取值范围,将多元转化为少元,直至单元。
由题中的恒成立条件着手,学生容易将其转化为自己熟悉的最值问题,并通过数形结合、直观想象,因而可得到:对任意实数x,不等式组恒成立,进一步可化简得到不等关系:但到此处,学生又遇到阻碍,止步不前。归其原因,变量过多、不等关系复杂,超出了高一学生的知识范畴。解决此类问题,应结合高一学生的实际学情,通过直观感受,借助几何直观和想象来感知函数的形态和变化,利用图形分析问题,建立形与数的联系。直观想象核心素养的形成过程中,学生能进一步发展提高数形结合的能力,感悟事物的本质,培养创新思维。因而教师应引导学生理解函数本质,数形结合,通过作图来观察函数f(x)图象所在位置。不难画出图像,如下图所示:
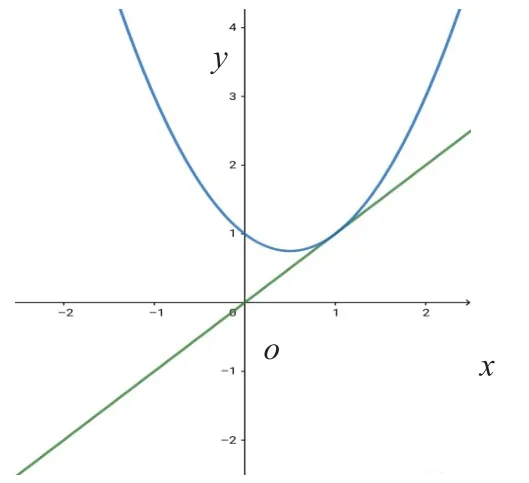
观察函数图像,直观想象,借助两函数的图像位置关系,建立形与数的联系,不难发现f(x)由于夹在两函数之间,即图像也夹在其之间,故必过它们的交点(1,1),从而可得到关系式再代入刚才的两个不等式,得到且有进一步代入可知故有解答完毕。
通过本题的学习,学生能体会多元函数最值问题的数学抽象过程,学会分析题中所给的数据,掌握条件的等价转化,构建适当的数学模型,数形结合,进而解决问题。
结合学生学情,为巩固和检验学生对该类多元最值问题的掌握,本人在课后设置了如下问题:
练习1:已知二次函数f(x)=ax2+bx+c(a,b,c∈R),满足f(-1)=0,对于任意的x∈R,都有并且当x∈(0,2)时有求函数f(x)的解析式。
该练习与例题在解题思路上有相似之处,有了上一题的解答经验,学生容易入手。结合例题,分析题中所给条件,类比方法,模仿解题,该练习能够进一步提高学生数学抽象的能力,再次体会直观想象、数形结合对研究函数问题的重要性。
二、代换消元,化繁为简
由上一问题的启发,本人对二次函数的多元最值问题进行深入探究。多元最值问题解决的另一常见方法,即是通过代换消元,化归为单变元问题,化繁为简,促进学生形成数学抽象、直观想象的数学核心素养。
题中条件同样简单明了,类比上一问题,分析题中所给数据“对任意的x∈R,有恒成立”,由该恒成立条件入手,学生容易利用二次函数图像,直观感知,数形结合,从而可以初步得到a,b,c三者间的不等关系和所求式子但与上一例题不同之处在于,本题中得到的并没有等式关系,而是不等关系,加上该式中仍有三个未知元,相较问题1有一定的难度,需要重新思考多变元问题的解决方法。但多变元问题的总体思想是一致的,即通过消元,达到少元直至单元解决问题。因此,本题中变元间只有不等关系,无等量关系,但不影响通过代换消元来处理a,b,c三者间的不等关系。在观察中学生不难发现,相较而言,变元c会结构单一,容易转换,于是有故可得原式此时,学生观察式子结果容易想到等价换元,构造新关系,建立新的数学模型,便有了如下解答:令再利用勾勾函数与基本不等式知识,得到当且仅当时,即b=4a时,原式取到最小值3,最终解决问题。
该练习的设置,是为学生巩固、提高对代换消元法来分析、处理二次函数多元最值问题。它与例题在数据的分析、处理上,所体现的数学思想和方法以及所要求的核心素养基本一致。故在此不再作具体展开。
三、主次变元,逐一解决
除以上常见的代换消元法来解决二次函数中多元最值问题以外,还有一类在多元问题中也时常遇到。如:
具体分析本题所给的数据,与前面两个问题比较,可以看到本题中有x,a,b三个变元,且相互之间似乎又找不到直接的联系。这样,就很难再用上述代换消元的方法解决问题。学生在解这类题时遇到的主要困难在于题目中不仅有多变元,且题中的存在、恒成立条件对每个变元都有要求,如若同时考虑三个变元,就会举步维艰。既然三个变元无法同时解决,就拆分逐一处理,故必须引导学生将三个变元进行拆开,分别当作问题的主元,其余先当作次元或常数来处理,再将存在、恒成立问题转化为最值问题,求出其对应的最值。可先将变元x看作问题的主元,即先考虑条件“存在实数使得不等式此时得到的成立”,学生比较容易将问题转化为是关于a,b的二元函数,再依次类比,分别再把a,b看作主元,转化为其最小值大于等于m的问题,从而解决问题。
学生解答本题时,容易利用换元将其转化为二次函数的绝对值最值问题,即则原命题等价于再记则原命题等价于再记从而原命题等价于
①当a=0时,
② 当a<0时,此时
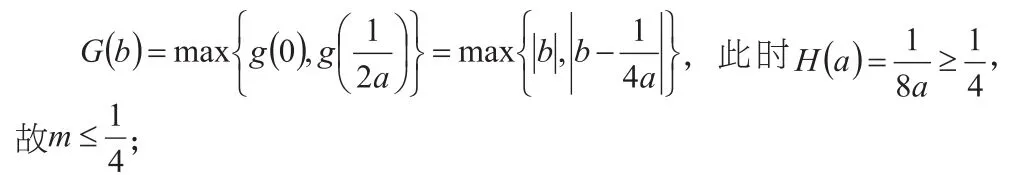
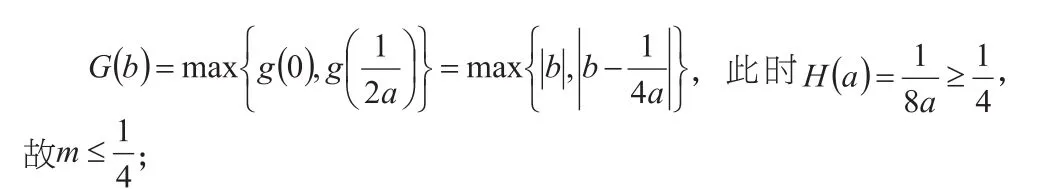
本题原本条件简洁,但结构复杂,学生较难入手。处理题中数据,将问题中的多元进行主次转换,逐一拆分,把问题转化成几个小的、同时又是学生掌握得较好的最值问题,再一一去解决,就会容易得多。此后的二次函数最值问题,则可结合函数图像,直观想象,恰当地分类讨论,数形结合便可解得
多元函数的最值问题有很多解决方法。函数问题的分析和解决,能使学生体会到数形结合、直观想象的重要作用,进一步提高对数据的分析、处理能力,培养学生的数学思维。不同问题的类比辨析,寻找共同之处,探究方法,学生的学习能力和核心素养都有所提高,这便是学习数学的意义和价值所在。
