“函”“方”互化，实现高效课堂——在中考复习中，如何运用函数与方程思想提高解题能力

广东省东莞市石排中学 邓沛森

在中考复习课中，提高课堂效率是一个重要环节，而怎样的数学课堂才是有效、甚至高效的呢？数学高效课堂应具备什么特征？

中考数学知识的考查过程中逐步加强数学思想方法的考查，数学思想方法是数学知识在更高层次上的抽象和概括，它蕴含于数学知识的发生、发展和应用的过程中。而函数与方程的思想方法作为基本的数学思想方法之一，在知识的互相联系，互相沟通中起到了纽带作用。抓住数学思想方法，善于迅速调用数学思想方法，更是提高解题能力根本之所在。因此，在复习时要注意体会教材例题、习题以及中考试题中所体现的数学思想和方法，培养用数学思想方法解决问题的意识。在中考复习过程中，“函”“方”互化，提高解题能力，实现高效课堂函数与方程思想共分为两个方面：函数思想与方程思想。

一、函数思想

函数思想，是抛开所研究对象的非数学特征，抽象其数学特征、利用函数的概念和性质去分析问题、转化问题和解决问题。方程思想，是从问题的数量关系入手，运用数学语言将问题中的条件转化为数学模型（方程、不等式、或方程与不等式的混合组），然后通过解方程（组）或不等式（组）来使问题获解。有时，还实现函数与方程的互相转化、接轨，使复杂问题简单化，达到最终解决问题的目的。

1．函数思想解决方程问题

例1 一次函数y=kx+b（k，b为常数，且k不为0）的图像如图所示，根据图像信息可求得关于x的方程kx+b=0的解为__________。

解答：∵一次函数y=kx+b过（2，3），（0，1）点，__________，__________，

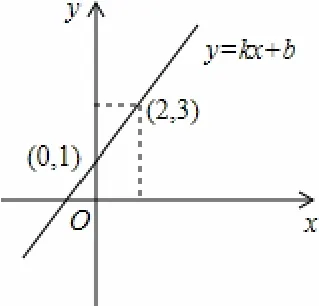
∵一次函数y=x+1的图像与x轴交于（-1，0）点，∴关于x的方程kx+b=0的解为x=-1，故答案为x=-1。

小结：函数解析式的函数值对应方程的根，就是该应函数图像与x轴交点的横坐标。

2．函数思想解决不等式问题

例2 如图，函数y=2x和y=ax+4的图像相交于A（m，3），则不等式2x＜ax+4的解集为______。

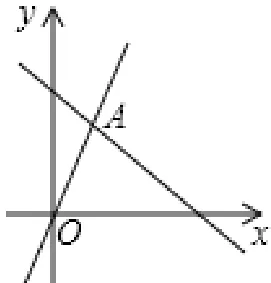
把A（m，3）代入y=2x，得2m=3，解得根据图像可得：当时，y=2x的图像在y=ax+4的图像下方。不等式2x＜ax+4的解集是故答案是

小结：判断函数值大于零还是小于零关键看函数图像在x轴的上方还是下方，上方函数值＞0，下方函数值＜0。判断一个函数值大于另一个函数值，看这一个函数图像是否在另一个函数图像的上方，在图像上方函数值大于在下方的图像的函数值。

3．函数思想解决实际问题

函数思想是有时运用运动和变化的观点，集合与对应的思想，分析和研究数学问题中的数量关系，建立函数关系或构造函数，运用函数的图像和性质去分析问题、转化问题，使复杂问题简单化，达到最终解决问题的目的。

例3 为改善生态环境，防止水土流失，某村计划在江汉堤坡种植白杨树，现甲、乙两家林场有相同的白杨树苗可供选择，其具体销售方案如下表：

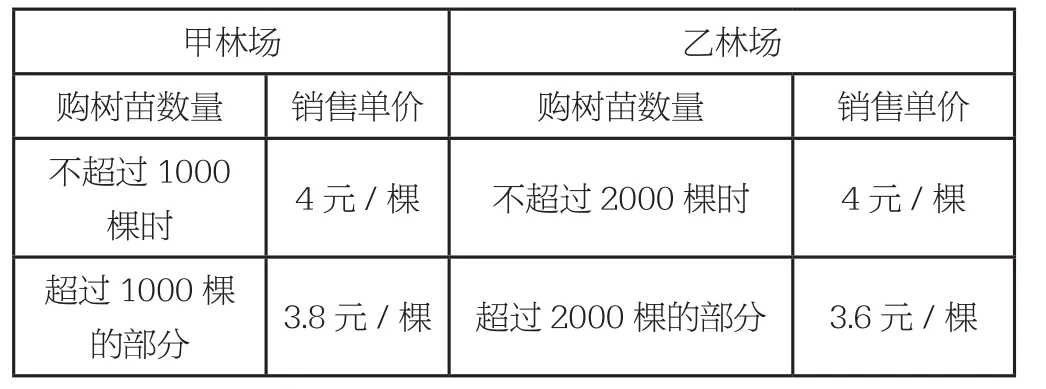
甲林场 乙林场购树苗数量 销售单价 购树苗数量 销售单价不超过1 0 0 0棵时 4元/棵 不超过2 0 0 0棵时 4元/棵超过1 0 0 0棵的部分 3.8元/棵 超过2 0 0 0棵的部分 3.6元/棵

设购买白杨树苗x棵，到两家林场购买所需费用分别为y甲（元）、y乙（元）。（1）该村需要购买1500棵白杨树苗，若都在甲林场购买所需费用为 元，若都在乙林场购买所需费用为___元；（2）分别求出y甲、y乙与x之间的函数关系式；（3）如果你是该村的负责人，应该选择到哪家林场购买树苗合算，为什么？

思路分析：（1）由单价×数量就可以得出购买树苗需要的费用；（2）根据分段函数的表示法，分别当0≤x≤1000，或1000＜x≤2000，或x＞2000，由单价×数量就可以得出购买树苗需要的费用，表示出y甲、y乙与x之间的函数关系式；（3）分类讨论，当0≤x≤1000，1000＜x≤2000时，x＞2000时，表示出y甲、y乙的关系式，就可以求出结论。

小结：用函数思想解决问题，在近几年中考中占有很大比重，许多省市的中考题都有这部分内容，尤其是用函数的观点看待方程（组）、不等式和几何知识等，利用函数解决实际问题，题型多样化，填空、选择、解答、综合题都有，主要考查学生应用函数知识分析、解决问题的能力，所以，实现“函”“方”互化，提高学生解题能力，实现高效课堂。

二、方程思想

方程思想是根据实际问题——数学问题——代数问题——方程问题，在数学的世界里，到处都是等式和不等式。哪里有等式，哪里就有方程；哪里有公式，哪里就有方程；求值问题是通过解方程来实现的……不等式问题也与方程是相近的且密切相关。函数的研究离不开方程研究.列方程、解方程和研究方程的特性，都是应用方程思想时需要重点研究的。

1．数与式中的方程思想

用方程思想解题的关键是利用已知条件或公式、定理中的已知结论构造方程组。

例4 如果单项式 -3x4a-by2与x3ya+b是同类项，那么这两个单项式的积是（ ）

A.x6y4； B.-x3y2； C.x3y2； D.-x6y4

本题通过同类项的相关定义，构造出方程组。

2．方程思想解决函数问题

两个一次函数图像的交点表示点在两条直线上的横坐标相同，纵坐标也相同。例如：求直线y＝x与y=3x-4的交点，就可以把两个二元一次方程组成方程组解得所以两条直线的交点坐标为（2，2），那么我们也可以在坐标系内画出这两条直线的图像，如右图所示，观察两条直线的交点，正是（2，2）。

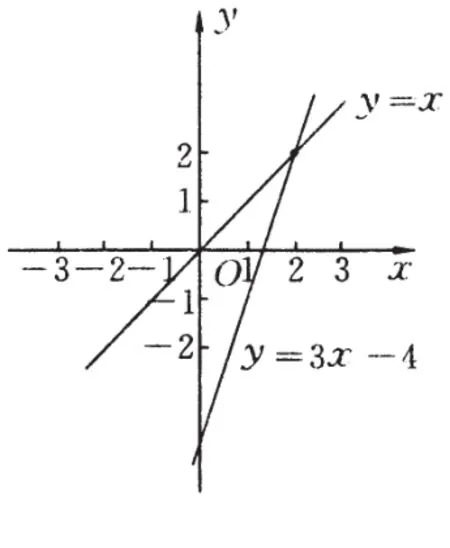
小结：两个函数图像的交点坐标就是对应函数解析式所组成的方程组的解。反过来，组成的方程组的解就是两个函数图像的交点坐标。

3．平面几何中的方程思想

例5 如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，则EF的长为_____。

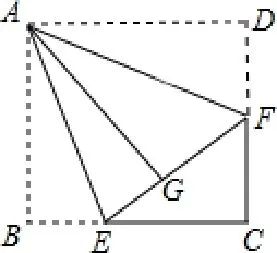
解：∵正方形纸片ABCD的边长为3，∴∠C=90°，BC=CD=3，根据折叠的性质得：EG=BE=1，GF=DF，设DF=x，则EF=EG+GF=1+x，FC=DC-DF=3-x，EC=BC-BE=3-1=2，在Rt△EFC中，EF2=EC2+FC2，即（x+1）2=22+（3-x）2，解得故答案为

评论：通过正方形、折叠相关的定理与性质，将平面几何问题，转化为方程思想问题。

小结：方程思想就是把问题中的已知量与未知量之间的数量关系，运用数学符号语言转化为方程（组）或其他形式的数学模型，使问题得到解决的思想方法。

（1）把问题归结为确定一个或几个未知数；

（2）挖掘问题中已知与未知数量之间的等量关系，建立方程或方程组；

（3）求解或讨论所得方程或方程组；

（4）检验并作出符合问题实际的回答。

方程的思想方法就是从问题的数量关系分析入手， 运用数学语言将问题中的条件转化为数学模型，然后通过解方程使问题获解。

函数研究是数学的主线，它用联系和运动、变化的观点研究、描述客观世界中相互关联的量之间的依存关系，形成变量数学的一大重要基础和分支。函数思想以函数知识做基石，用运动变化的观点分析和研究数学对象间的数量关系，使函数知识的应用得到极大的扩展，丰富并优化了数学解题活动，给数学解题带来一股很强的创新能力。

函数思想与方程思想的联用。在解综合题中，解决一个问题常常不止需要一种数学思想，而是两种数学思想方法的综合运用．例如函数思想与方程思想的综合运用，它们之间的相互转换一步步使问题获得解决，转换的途径为函数——方程——函数或方程——函数——方程等。所以实现“函”“方”互化，大大提高学生解题能力，实现高效课堂。