一种基于局部扩展优化的重叠社区发现算法*

李 慧，杨青泉，王慧慧

(首都师范大学教育技术系，北京100048)

1 引言

复杂网络是现实世界中复杂系统的高度抽象，如生物系统中的新陈代谢网、蛋白质相互作用网，科技系统中的因特网、万维网，社会系统中的科学家协作网、电子邮件网等。除了小世界特性和无标度特性外，社区结构是复杂网络最重要的拓扑结构特征之一，已成为多学科交叉研究的热点［15］。挖掘复杂网络的社区结构，对分析网络的拓扑结构、理解网络的功能及预测网络的行为等具有重要的理论意义和实用价值。

2002年，Girvan和Newman首次提出著名的社区发现算法GN，引起了国内外研究者的广泛关注，随后在社区挖掘领域取得了一系列创新性研究成果［6，7］。经典的社区发现算法包括图分割、层次聚类、谱聚类、模块度优化及基于模型的方法等，主要围绕非重叠社区探测问题展开，具有一定的局限性:(1)需要网络的结构信息、社区规模和社区划分数目等先验知识;(2)全局搜索和计算影响算法的运行速度，计算复杂度高;(3)难以发现复杂网络中社区的重叠属性。2005年，Palla等人［8］拓展了传统社区模式，允许节点同时属于多个社区，提出基于派系过滤的重叠社区发现算法，开启了重叠社区结构识别的研究热潮，迅速成为社区挖掘的前沿研究热点。派系过滤、标签传播［9］、局部边聚类优化［10］、局部扩展优化［11，12］等重叠社区发现方法，无需完整的网络结构信息等先验知识，基于局部拓扑结构揭示网络整体或局部的社区结构，在计算代价、网络局部社区特性挖掘等方面具有更多优势。

基于局部扩展优化的重叠社区发现算法，通常从不同种子节点开始，根据给定的优化函数，探索种子所在的局部社区结构，由所有局部社区结构融合成整个网络的重叠社区结构，代表性算法有LFM(Local Fitness Maximization)算法［11］和 GCE(Greedy Clique Expansion) 算法［12］。Lancichinetti等人提出的基于局部结构适应度的社区扩展方法LFM是第一个能同时发现重叠社区及其层次结构的算法。LFM随机选取初始种子节点，基于适应度函数的贪婪优化，从种子节点开始逐步合并使节点适应度增加的邻居节点或删除使其减小的节点，直至适应度函数为负值，得到种子节点所在的局部社区;搜索过程中，任意节点可以被多次访问，使得节点能够包含在多个社区，从而发现网络的重叠社区结构;调节分辨率参数可以获得社区的层次结构。LFM算法对初始种子节点较敏感，随机选取种子节点可能导致划分结果的不稳定，误选种子节点将不能得到合理的社区结构;当初始种子节点位于稀疏的重叠区域时，会出现左右摇摆的社区漂移问题，带来大量的计算冗余;在局部扩展过程中存在删除节点操作，可能导致最初的种子节点被删除，使得扩展过程不再围绕该种子进行，违背社区的“局部性”［13，14］。GCE 算法首先选取所有节点规模不小于k的最大团作为种子，然后采用贪心策略从种子开始逐步添加适应度函数最大的节点，直至适应度函数不再增大，得到种子所在的局部社区Ct;计算 Ct与已检测到的社区 C1，C2，…，Ct－1之间的距离，如小于给定的阈值则舍弃Ct，否则保留Ct。GCE算法选取的种子存在相似性，导致不同种子扩展得到相似或者冗余的社区。在种子扩展过程中存在社区删除操作，使得最终获得的重叠社区只能覆盖整个网络的一部分节点，即算法结束后存在一部分社区标签未知的节点。

针对上述问题，本文提出一种基于节点聚集系数和适应度函数的局部扩展式重叠社区识别算法CFLEM(Local Expansion Method based on Clustering-coefficient and Fitness)，主要步骤包括基于节点聚集系数的种子选取、基于适应度函数最大化的自然社区识别以及社区结果的对比与合并。本文的主要贡献:

(1)基于节点聚集系数的种子过滤规则能够得到局部性好、结构稳定的自然社区识别结果，避免了结果抖动性问题。

(2)对社区识别结果的对比与合并，能够在保证高社区覆盖率的前提下尽量减少冗余社区。

本文分别在 LFR(Lancichinetti-Fortunato-Radicchi)人工网络和真实网络数据集上对CFLEM算法的性能进行测试，并与具有代表性的基于局部扩展优化的重叠社区发现算法进行对比分析，结果表明本文算法在稀疏程度不同的网络上均能发现较高质量的重叠社区结构。

2 基本概念及定义

2．1 社区

复杂网络可以建模为图 G=(V，E)，其中V={v1，v2，…，vn} 为节点的非空有限集，n为节点数;E={e1，e2，…，em} 为边的非空有限集，m 为边数。节点vi的度定义为该节点的邻居数，表示为，其中A是图G的邻接矩阵。社区是图G的节点内聚子图，其内部节点连接紧密，不同社区间的节点连接稀疏，反映了网络的模块化与异质性。

定义1(社区相似度) 给定图G中的任意2个社区C1和C2，社区相似度定义为:

δ(C1，C2)表示社区C1和C2的相似程度，取值范围为［0，1］，值越大社区相似性越高。

2．2 适应度函数

其中，f(C+{v})和f(C－{v})分别表示在同分辨率情况下的节点v在社区C内部和在社区C外部的结构适应度。随着分辨率α的增加，网络逐渐呈现细粒度化趋势，直至每个节点自成一个独立的社区。根据节点适应度f(v)可以判定节点v是重叠节点还是离散点。

2．3 聚集系数

定义4(节点的聚集系数) 假设图G=(V，E)中节点vi有ki个邻居节点，则节点vi的聚集系数CCi定义为其所有邻居节点之间实际存在的边数Ei与可能存在的最大边数ki(ki－1)/2的比值，表示为:

节点vi的聚集系数CCi是衡量网络集团化程度的重要参数，用于描述节点的聚集程度，即与节点vi相连的两个节点也相连的可能性。节点的聚集系数越大，表明其局部聚集性较高，成为干扰点和离散点的概率相对越小。

3 算法思想与分析

本文综合运用网络的拓扑结构信息和节点的属性，提出一种基于局部扩展优化的重叠社区发现算法，首先根据网络中节点的拓扑特征(聚集系数)选取种子节点作为初始社区，然后采用贪心策略将初始社区扩展为局部自然社区，最后对比、合并不同的局部社区获得重叠社区结构。具体过程见算法1。

算法1CFLEM算法

输入:网络G=(V，E)，分辨率参数α。

输出:重叠社区结构C。

步骤1初始化，C=。

步骤2根据种子选取算法，得到种子集合S。

步骤3当S≠时，选择某个种子，执行步骤4;否则执行步骤6。

步骤4种子扩展成局部自然社区D，调整种子集合S。

步骤5将D加入到C中，返回步骤3。

步骤6对比、合并局部社区。

步骤7返回重叠社区结构C，结束。

3．1 种子选取

种子选取是基于局部扩展优化的重叠社区发现算法的关键步骤，对社区识别结果的影响不容小觑。LFM算法随机选取种子节点，不可避免地导致社区发现结果不稳定。GCE算法选取网络中所有节点规模不小于k的最大团作为种子，避免了社区发现结果不稳定的问题。但是，较小的k容易导致种子规模过大、扩展得到的局部自然社区数增多，形成冗余社区;较大的k则容易导致局部自然社区数减少，社区发现结果的覆盖率降低;由于不同最大团之间存在相似性，导致不同种子扩展得到的局部社区是相似的甚至冗余的。

针对上述问题，本文借鉴从中心节点出发进行社区发现可以提高社区识别质量的思想［15］，提出了选取网络的核心节点作为社区划分的种子节点。核心节点通常位于网络中节点连接紧密的区域，对信息传播的贡献较大。网络中的不同社区与核心节点之间往往存在对应关系，因此本文采用节点的聚集系数作为拓扑特征指标来选取种子节点，具体过程见算法2。

算法2种子选取算法

输入:网络 G=(V，E)。

输出:种子集合S。

步骤1初始化，S=。

步骤2将节点按聚集系数从大到小排序，形成候选种子列表L，所有节点初始化为无标记。

步骤3取出L中第一个节点v，如果v未标记，设置标记并将其加入种子集合S。

步骤4标记v的邻居节点N(v)，从列表L中移除已标记的节点集

步骤5当L≠时，继续执行步骤3;否则，输出种子集合S。

种子选取算法能够在网络中发掘彼此分散的、局部聚集系数大的节点，通过这些种子节点扩展而成的自然社区的局部性好，社区发现结果对全网络的覆盖率高。

3．2 局部扩展

在扩展阶段，CFLEM算法通过最大化局部社区适应度函数的方法对种子节点进行扩展得到自然社区，主要包含两个步骤:添加当前社区C的邻居中f(v)为正值的节点和删除社区C中f(v)为负值的节点，使得社区C的适应度函数f(C)达到最大。CFLEM算法采用批添加节点和批删除节点的方法扩展社区C，即首先遍历C的每一个邻居节点v并记录其f(v)，在遍历结束后将f(v)＞0的节点统一加入社区;然后再遍历社区C，记录其每个节点v的f(v)，遍历结束后将f(v)＜0的节点统一移出社区。具体过程见算法3。

算法3局部扩展算法

输入:网络G=(V，E)，种子s，分辨率参数α。

输出:社区C;

C←{s};

for each neighbor vertex v of C do

计算节点适应度f(v)

end for

将节点适应度值大于零的邻居节点统一加入社区C;

for each vertex v of C

计算节点适应度f(v)

end for

将所有适应度值小于零的节点统一移出社区C;

返回C，结束。

3．3 社区合并

重叠社区发现算法允许2个不同社区包含若干公共节点，因此种子扩展得到的自然社区之间存在一定的相似性。当相似性达到一定程度时，可能产生“过度重叠”现象，因此有必要对社区发现结果进行后处理，发现其中的冗余社区，简化社区结构。

针对局部扩展得到的自然社区，CFLEM算法采用公式(1)计算任意2个社区的相似度，即以它们之间共同节点在较小的社区中所占的比例来衡量社区是否需要合并。如果δ大于某个给定的阈值ε，则判定需要合并社区。具体过程见算法4。

算法4社区合并算法

输入:社区集合{C}，阈值ε。

输出:社区集合{C'}。

for each c in C do

if{C'}中存在社区c'和c的相似度大于ε

将c合并至社区c'

else

将c加入社区集合{C'}

end if

end for

返回{C'}，结束。

3．4 算法时间复杂度分析

CFLEM算法的实现过程可以概括为三个阶段:(1)根据聚集系数调整种子节点并生成初始社区;(2)将每个初始社区扩展为局部社区;(3)对比合并社区。阶段(1)需要计算种子及其邻居节点的聚集系数，最坏情况下计算给定网络中每个节点的聚集系数时，时间复杂度为O(d2)，其中d为节点的平均度。阶段(2)将每个初始社区扩展为局部社区的时间复杂度为O(n2)，n表示社区的节点规模，若存在M个种子节点和初始社区，那么阶段(2)的总时间开销为 O(M珔n2)，珔n 表示平均社区节点规模。当分辨率参数α较小时，新节点的加入导致f(C)增大的机会更大，使社区C能够接纳更多的节点，达到更大的社区规模(即珔n比较大)，时间复杂度随之增大，最坏情况下时间复杂度为O(N2)，其中N为网络中节点的规模。反之，当α越来越大时，新节点的加入对增大f(C)值的贡献越小，使新节点加入当前社区的难度增大，从而形成较小规模的社区(即珔n比较小)，时间复杂度将逐渐趋于线性O(N)。阶段(3)最坏情况下的时间复杂度为O(M2)。因此，CFLEM算法的时间复杂度在最坏情况下为O(d2+N2+M2)。在复杂网络中，由于节点的平均度dN，种子的个数M ＜N，因此总的来说，CFLEM算法的时间复杂度为O(N2)。

4 实验结果与分析

本文采用不同规模、不同属性的人工网络和真实网络数据集测试算法性能，设置如下2类实验:

(1)测试当节点数及混杂系数变化时算法性能的变化规律，网络数据为LFR网络数据生成器［16］模拟生成的人工网络。

(2)比较各算法发现不同网络结构的性能，网络数据为6个不同规模、不同类型的真实网络数据集。

为了实现算法的对比分析，采用模块度函数Qo作为度量指标。Newman等人［17］最先提出的模块度函数Q已成为评价不可重叠社区发现算法的重要指标。针对重叠社区划分的质量评价，Shen等人［18］提出了扩展模块度函数Qo，其函数表达式为:

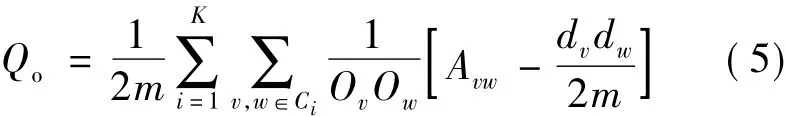
其中，v、w为节点;K是网络包含的社区数;Ov是节点v所属社区的数目;Avw为邻接矩阵A中的元素，如果节点v、w相连，则Avw=1，否则Avw=0;m=为网络中边的数目;d是节点v的度值，v表示在随机网络中节点v和节点w之间存在连边的可能性。

当复杂网络的社区内部节点连接越紧密而不同社区间节点连接越稀疏时，Qo函数取值越大，算法社区划分的准确率越高，算法性能越好。

4．1 不同清晰度的人工网络上算法性能的比较

为了比较具有不同清晰度网络上的算法性能，采用不同规模的人工网络测试CFLEM算法与LFM算法随网络节点数及混杂系数变化的规律。4类人工网络由LFR网络数据生成器模拟获得，分别为稀疏网络小社区(SS)、稀疏网络大社区(SL)、稠密网络小社区(DS)和稠密网络大社区(DL)，对应的LFR参数(网络节点数N、节点平均度值珋k、节点最大度值kmax、社区最大规模Cmax、社区最小规模Cmin、节点度指数t1、社区规模指数t2、重叠节点数On、重叠节点属于社区数Om和混杂系数μ)见表1。其中，混杂系数μ反映了网络社区结构的清晰程度，该值越小社区结构越清晰，当μ∈［0．7，0．9］时网络的社区结构通常不明显，因此分别在4类网络上生成μ∈［0．1，0．6］的测试网络。

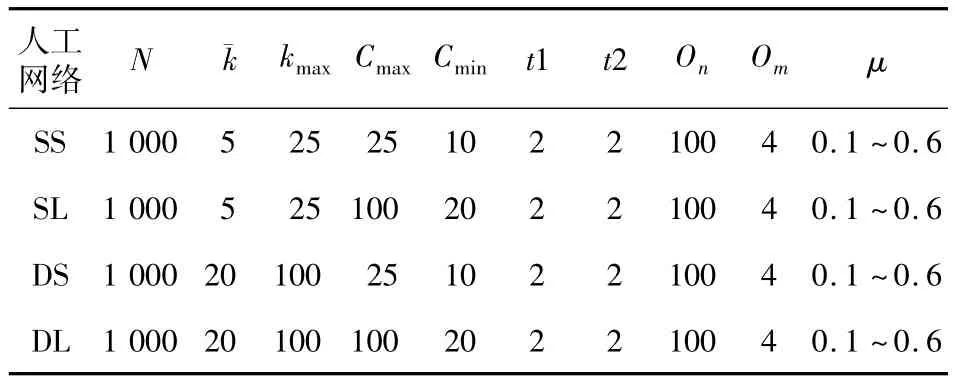
Table 1 Parameters setting of synthetic networks表1 人工网络数据集的参数设置

实验针对不同算法设置不同的参数，并选取各参数下Qo值中的最大值作为最终结果进行对比。具体地，LFM 算法中，设置参数 α ∈［0．8，1．6］，取值间隔为0．1，运行次数r=3;CFLEM算法中，设置参数 α ∈［0．6，1．2］，ε ∈［0，0．9］，取值间隔均为0．1。随着网络规模(节点数、边数)的增加和混杂系数μ的增大，CFLEM算法与LFM算法在不同清晰度的4类人工网络上的实验结果如图1所示。

总体来看，随着混杂系数μ的增加，网络中社区的内部节点连接社区外部节点的机会增大，导致社区结构变得模糊，社区发现的难度变大，使得2种算法社区发现结果的质量降低，因此在4类人工网络上2种算法得到的Qo值均有不同程度的下降。其中，LFM算法相对于CFLEM算法的下降幅度更大，尤其在稀疏网络小社区(SS)和稀疏网络大社区(SL)中，当社区结构越来越不明显时，CFLEM算法展现出一定的优势。

从图1中可以看出，CFLEM算法在绝大多数网络上的社区发现结果要好于LFM算法，原因在于CFLEM算法选取网络中的核心节点作为种子，扩展得到的社区具有更好的局部性;LFM算法则随机选取种子，在局部扩展时将节点适应度函数为负的种子删除，导致扩展过程不再围绕该种子进行，从而得到局部性较差的社区。

对比CFLEM算法、LFM算法在稀疏网络小社区(SS)、稀疏网络大社区(SL)、稠密网络小社区(DS)和稠密网络大社区(DL)的社区识别结果，2种算法在稀疏网络上的准确度更好。原因在于:当固定混杂系数μ时，稀疏网络相对于稠密网络的社区结构更为明显，能够较准确地发现其中的自然社区。

综上所述，与FLM算法相比，CFLEM算法在不同清晰度的4类人工网络数据集上能够取得较高质量的社区发现结果。

4．2 不同结构的真实网络上算法性能的比较

为了对比分析算法CFLEM、LFM、GCE的结构发现能力，测试网络采用6个不同规模、不同类型的真实网络数据集:人物关系网络(Karate、Football)、动物关系网络(Dolphins)、游戏网络(Risk)、论文合作网络(CA-GrQc)和产品销售记录网络(Amazon)，其基本信息见表2，更多信息参见http://www-personal．umich．edu/～ mejn/netdata、http://snap．stanford．edu/data 和 http://en．wikipedia．org/wiki/Risk_(game)。

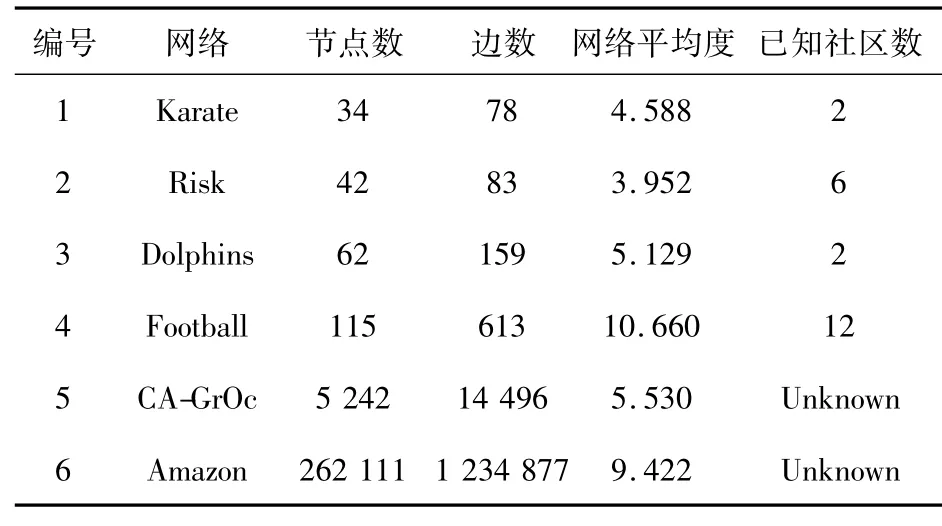
Table 2 Datasets of real-world networks表2 真实网络数据集表

由于绝大多数真实网络数据集的社区结构是未知的，因此除了重叠模块度函数Qo外，本文还采用社区连接密度和网络覆盖率Ro来综合评价算法性能。社区连接密度Do定义为:

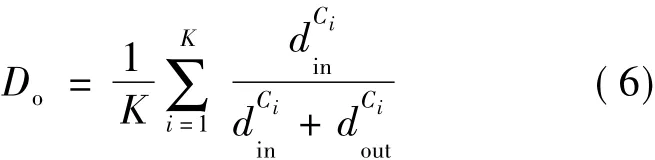
其中，K为网络中的社区数，Do可以看作当α=1时网络中所有K个社区的局部结构适应度的平均值。

网络覆盖率Ro定义为:

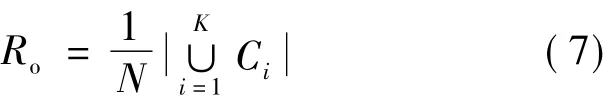
其中，N、K分别为网络中的节点数和社区数，Ci表示第i个社区。社区连接密度Do和网络覆盖率Ro的取值均为［0，1］，值越大表明社区发现结果的质量越好。

对于 GCE 算法，设置其参数 α∈［0．8，1．6］，取值间隔为0．1，参数 k∈{3，4}，ε =0．6;CFLEM算法和LFM算法的参数设置与4．1节相同，并选取各参数下的最优结果进行对比。各算法在6个真实网络下的社区发现结果质量的Qo、Do、Ro值分别如图2a、图2b、图2c所示，其中横坐标轴表示真实网络数据集的编号，纵坐标轴分别表示3种算法在对应数据集上的社区发现结果的Qo、Do、Ro值。

由图2a可以看出，针对大部分真实网络，CFLEM算法得到的Qo值最优，二者较GCE算法具有较为明显的优势，表明CFLEM算法能够得到质量较高的重叠社区结构。

图2b表明，CFLEM算法在所有真实网络数据集上都取得了最高的社区连接密度Do，LFM算法得到的社区连接密度相对较低，原因在于CFLEM算法的种子节点选取方法优于LFM算法随机选取种子的方法，社区扩展过程围绕所选种子进行，得到了局部性较好的社区。

如图2c所示，CFLEM算法和LFM算法在不同网络上均具有较高且较稳定的网络覆盖率Ro，而GCE算法的Ro值较差且波动较大。LFM算法从无社区标签的节点中随机选取种子，在算法结束时仅剩余极少数标签不明确的节点，因此其社区覆盖率很高。与GCE算法相比，CFLEM算法所选种子之间的相似性更低，扩展得到的自然社区能够覆盖更多的网络节点;而且CFLEM算法对社区发现结果进行了后处理，合并冗余社区，保证了网络的高覆盖率，更符合社区的真实情况。GCE算法将冗余的社区直接舍弃，导致算法结束时存在一部分社区标签未知的节点，社区发现结果的质量较低。

综合来看，在6个真实网络数据集上，CFLEM算法社区发现结果的质量最高，LFM算法的结果质量次之，GCE算法的结果质量相对较低。3种算法的结果均存在不同程度的波动，但CFLEM算法的波动相对较小。

5 结束语

本文提出一种基于节点聚集系数和适应度函数的局部扩展式重叠社区发现算法——CFLEM。该算法选取网络的核心节点作为社区划分的种子节点，采用贪心策略将种子扩展为局部自然社区，然后对社区发现结果进行后处理，合并冗余社区从而保持社区的高覆盖率。在LFR人工网络和真实网络数据集上的实验结果表明:与LFM、GCE算法相比，CFLEM算法能够在稀疏程度不同的网络上获得更优的社区发现结果。下一步的工作将拓展CFLEM算法至加权网络中，致力于加权网络的社区发现问题研究。