三维激光扫描系统参数标定及成像测试

李晋 刘家顺 黄苏军 谢尚佐

摘要 三维激光扫描技术是一项新兴而且前景非常可观的技术，在逆向工程、工程测绘、三维重建及虚拟现实等领域应用日益广泛，在三维激光扫描系统中各参数的标定对于实验结果往往产生影响是决定性的，本文主要对三维激光扫描的系统参数进行标定以提高精度，并提出了一种新的标定模板与算法，针对低成本三维激光扫描系统提出了降低误差的方法，实验结果表明，该标定方法较好的实现了三维激光扫描系统的参数标定和精度提高，与国外同类型低成本三维激光扫描仪Ciclop相比，精度有显著提升。

[关键词]三维激光扫描 激光三角法 系统参数标定精度

1 引言

三维激光扫描系统由于能够快速恢复物体的三维模型，并且精度较高，近年来在工程测绘、模型分析和虚拟現实等领域广泛应用，国内外许多实验室进行大量研究，基于激光扫描技术的三维重建技术成为研究热点。

本文主要介绍一种低成本三维激光扫描系统的参数标定及成像，主要对基于线结构光原理的三维激光扫描系统中的并针对校准过程中的相机标定与激光三角法扫描算法进行改进提出一种新的标定模板，并在最后对于改进后的扫描点云结果进行简要分析，与原标定模板扫描结果进行对比，可看出其在精度和误差控制上有显著提高。

2 本文三维激光扫描系统原理

本文中研究的低成本三维激光扫描系统正是基于此方法改进的，主要采用两颗一线型激光发射器和一颗罗技C270网络摄像头组成，其旋转平台采用42步进电机驱动，其扫描原理使用两颗激光发射器，使得被扫描物体在每次扫描时均可通过两次线型扫描。我们研究了以下几种可能：

2.1 只有一个激光发射器与摄像头且处于同一水平面

情况如图1所示。

图中的Pl点是光束射到投影屏高度的中点。Pl点的投影Pl点到摄像头光学中心的距离为摄像头的距离。因此，Pl点的求解可以直接带入上文单点激光三角测距的公式（2-4）中求解出真实距离。以下公式是对投影画面中任意一点P2的求解：

公式中Q2'y是点Q2在光敏元件上的实际高度，同理Ql'y，它们的求解可根据像素坐标乘以像素高度。

2.2 只有一个激光发射器与摄像头且不处于同一水平面

情况如图2所示。

对于这种情况可以假设处于同一水平面，其运算的过程同上，pl点由上文公式求到并作为参考点，pl到p2的实际距离通过算法可求出，在此不赘述。有图可知变化量为a角，己知量（dl，B，O，）通过三角形转换关系可得出a的值，其d2的表达式如下：

得到d2（C到P2的距离），求d（激光器Laser到P2的距离）须R（A到Laser）的长度，由公式可知tana=m/d2，则d=d2-d2。

以上的所用参数在实际的测量中，很难把握它的精度，且参数精度对实验结果有着直接的影响，比如安装好激光器后对它的悬臂长的测量就会存在误差。

2.3 两个激光发射器与摄像头且不处于同一水平面

本文三维激光扫描系统正是基于此种结构设计的，在每次扫描周期内均可通过至少两次激光扫描，每一侧激光发射器扫描原理同上文所示，此处不再赘述，本文两激光器的位置关系如图3所示。

3 系统参数标定

3.1 相机参数标定

三维激光扫描系统在扫描物体获得一系列点云数据前最为关键的一步便是对摄像机的参数进行标定。相机参数的标定就是将二维图像坐标中的点对应到空间中物体的三维坐标，并找到二者的关系，通过二者的关系从而找到相机的参数并将其标定提高系统的精准度。

3.2 本文提出的标定模板

在标定过程中可以看到，此种标定方法需要将标定板在不同角度至少获取三张图片才能进行校准，对于本三维激光扫描系统其标定过程较为繁琐，且对于用户使用有一定难度，为了能够迅速准确的得到相机内外参数，我们改进选择了如图4标定模板。

该标定板将77个标准的原白点印在标准黑色平面板上，呈阵列分布，且每相邻的两个白点的真实距离15mm。只需要将世界坐标系建在标定板上，即选取某一个圆定点为世界坐标系的圆心与标志点阵列的行列方向重合，Z轴垂直于标定板，即可确定全部标志点在世界坐标系下的坐标值。

在此，因为使用传统的曲线拟合定位圆心方法对背景环境要求较高，当环境噪声较大时，会导致精度下降，鲁棒性较差，因此我们改进引用基于CNN的激光圆形边缘提取算法以确定标定板各圆形圆心。

3.3 标定结果分析

本文所采用的算法与张氏标定算法所用的模板不同，使用改进后的孟.胡方法基于曲线拟合，并且不需要任何匹配，而张氏标定算法在摄像机的标定过程中需要不断移动标定板拍摄各个角度的图像，这一过程略加繁琐，张氏标定过程如图5所示。

本标定系统采用罗技C270摄像头，像素为500万。为确保本文改进后的标定板的精度对比原有标定板有所提高，为此本文采用如下方法进行了结果分析：

（1）在标定过程中可得到标定矩阵、相机的内外参数矩阵，以及在当前摄像机参数下标定板上圆点圆心对应的图像坐标值。

（2）将圆形标定板上各个圆心的图像坐标理论值和实际对应的坐标值进行比较。

（3）分析比较结果并计算标定板上所有点的平均误差以及最大误差。

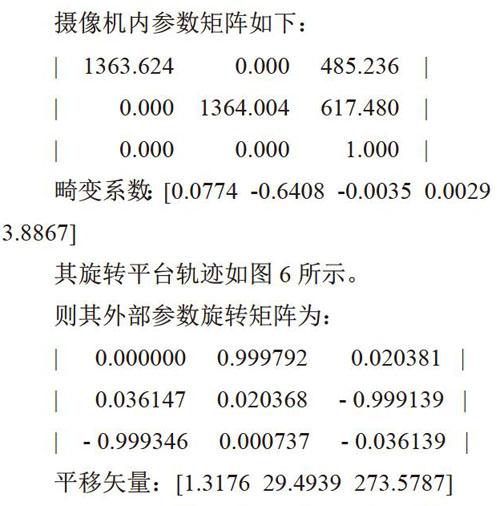
摄像机内参数矩阵如下：

1363.624

0.000 485.236

0.000 1364.004 617.480

10.000

0.000

1.000

畸变系数[0.0774 -0.6408 -0.0035 0.00293.8867]

其旋转平台轨迹如图6所示。

则其外部参数旋转矩阵为：

1

0.000000 0.999792

0.020381 l

1

0.036147

0.020368

- 0.999139

- 0.999346

0.000737

- 0.036139

平移矢量：[1.3176 29.4939 273.5787]

通過标定结果可以看到产生标定误差的主要是因为摄像机的像素不高，扫描环境光照不理想以及镜头的噪声水平很高，从前面的分析数据可知改进后新的标定板明显提高了扫描的精度要求。

4 实验结果分析

4.1 结果分析

采用匹配算法将扫描得到的点云进行匹配，在点云采集过程中出现孔洞时，可对针对特殊位置进行重复扫描，然后进行进一步匹配，得到更加完整的三维模型。

在采用本文提出的标定模板重新标定后，得到物体的扫描图像如图7。

运用前面提到的光条中心提取算法，即将光条中心提取算法应用于三维激光扫描仪中，以及摄像头的标定算法。重新对模型扫描如图8。

通过上面扫描的两个完整模型可以看出，本文提出的应用于低成本三维扫描仪的摄像机标定模板算法与图像中激光光条的中心提取算法取得了较好的效果，所需硬件均可3D打印，方便用户自行搭建系统，操作简单。

4.2 误差分析

可以造成三维激光扫描系统误差的影响因素较多，主要可以分为以下三类：仪器的系统误差、目标物体的反射面材料与外界环境条件的影响。

本文中采用被扫描物体放置在旋转平台的方式进行扫描，因为当电机步进过快是，此时摄像头拍摄的图像会产生一定拖影现象，导致线型激光器在图像中的光条过厚，降低了中心提取的精度，因此本文设定电机步进不应超过某一阈值，在一定程度上降低了误差。

另一方面，由于涉及两个线型激光器和摄像头，因此三者与被扫描物体的相对关系也会给扫描精度带来影响。研究显示扫描时线型激光器应与摄像头保持尽可能大的倾角，以保证扫描范围，此时30°-50°之间的夹角较为合适。

通过原理分析得出，本文改进的标定板和中心提取算法分别降低了其误差，摄像头的标定参数精度进一步提升，在扫描过程中，可通过修改摄像头外部参数来保证拍摄质量，降低背景环境带来的噪声影响，误差可进一步降低。

5 结论

本系统的硬件组成前面已有介绍，软件平台以Horus和Meshlab为工具。其配套的Horus软件是由BQ技术公司发布的开源软件，为Ciclop 3D扫描仪提供额外的功能。通过设置参数扫描自动生成通用的标准格式数据。生成后的点云数据导入到Meshlab软件中优化处理。

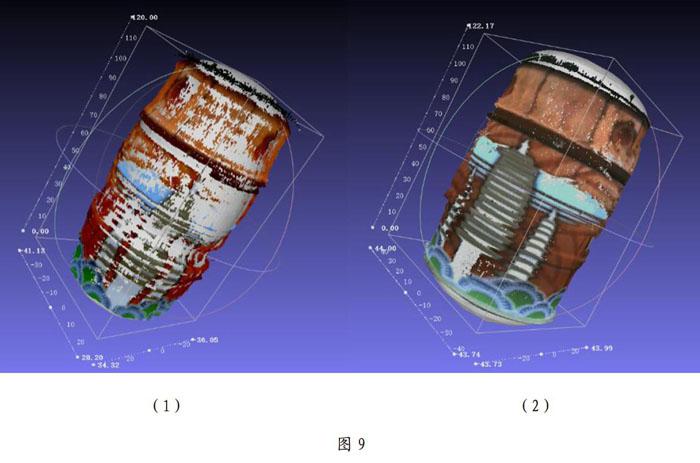
从图9中对比可以明显看出，本文中提出的标定模板及算法结果更佳。通过以上的两次的扫描模型可以看出，本文提出的针对基于低成本三维激光扫描系统的摄像头标定模板算法取得良好的效果，同时与原扫描系统Ciclop对比，其扫描结果不如本算法，在本文提到的标定模板校准后，模型误差显著降低。

参考文献

[1]付培.低成本三维激光扫描仪系统关键技术研究[D].哈尔滨工业大学硕士论文，2 010： 14-15.

[2]陈西，摄像机标定与三维重建研究[D].北京化工大学硕士论文，2007： 5-12，

[3]曲学军.基于空间平行直线束的CCD摄像机内外参数标定[J]，计算机工程与技术，2010.

[4]林育斌，基于计算机视觉的三维重建技术的研究[D].天津大学硕士论文，2010： 19-22.

[5]刘枝梅.结构光测量系统中光条中心的提取算法[J].北京机械工业学院学报，2009.