基于模块化设计的嵌入式伺服控制软件的研究

栾婷

摘要 本文研究一种模块化的嵌入式软件闭环算法的设计方法，分析了传统闭环算法设计的不足之处，给出了模块化闭环算法的设计理念和设计方法，并详细给出了几种闭环运算中常用的运算类型的模块化封装方法。在完全采用模块化设计方法后，缩短了伺服系统嵌入式控制软件的编写和调试时间，在提高效率节省资源的同时，也提高了伺服控制软件的可靠性。

[关键词]模块化 嵌入式 伺服控制

1 概述

伺服控制器是伺服系统的数字电子控制补偿装置，伺服控制器接收控制系统发出的数字指令信号，在伺服系统地面测试、发射准备、飞行等阶段，通过控制器内部的嵌入式软件运算，实现伺服系统内部信号采集、数字闭环控制、数字零位补偿及校正和与控制系统的通讯等功能。伺服系统总体要求伺服控制器嵌入式软件的闭环算法调整编写速度要快，出错次数要少，整体可靠性要高。为此伺服系统控制器的嵌入式软件进行了以提高可靠性为主要目的的软件模块化设计。

2 伺服系统嵌入式软件组成

本课题中伺服系统数字控制器以DSP（TMS320F2812）为计算平台，采用15 53B总线进行通信，采用TI公司为此配套的编译软件CCS来编写、调试和烧录程序。

伺服控制器软件的任务就是实现伺服系统与总线系统之间的通信，接收并执行BC的控制指令，并向BC发送伺服系统状态信息;定时采集伺服系统数据并按指定格式传送给总线系统;定时对采集的信号进行多项式擬合;定时对拟合后的冗余信号进行冗余表决，表决的结果作为数字闭环控制算法的反馈信号;定时接收BC发送的控制指令数据，进行伺服系统的数字闭环控制及补偿;同时软件具备初步的故障诊断及余度管理功能。

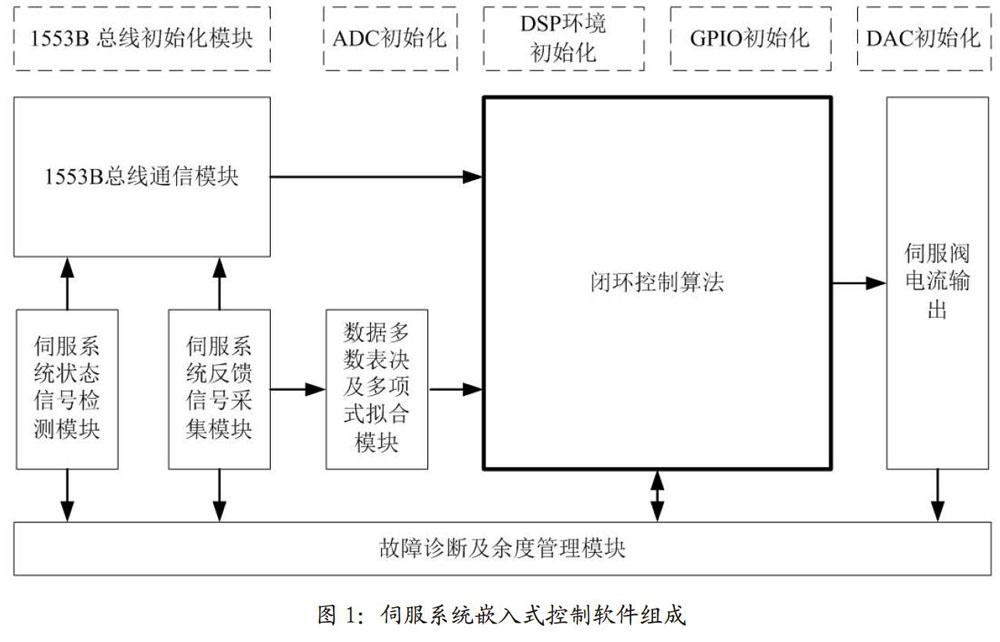
伺服系统嵌入式控制软件的主要组成如图l所示。

各模块分别执行自己的功能，进行模块间数据交互，执行闭环控制算法，完成对伺服阀的控制。

闭环控制算法通常需要进行三冗余反馈数据表决、拟合、故障诊断和余度管理等运算，闭环控制的步骤很多，如果还把闭环控制算法当成一个基本模块来编写，必然会使软件的执行步骤和复杂度大大增加。这不仅增加了嵌入式软件编写人员的工作量，在伺服系统调试过程中，也会不可避免的增加因软件编写错误而导致的无效启机试验，因此而造成大量有效时间浪费和不必要的经济损失。

为此，针对伺服系统闭环控制框图的特点，专门对伺服控制器嵌入式软件的闭环控制部分进行了模块化细化设计。

3 传统设计方法及技术改进点

3.1 传统闭环运算程序设计方法

传统的闭环计算方法把闭环控制框图当成一个基本软件模块来设计，主要采用的是面向过程的编写方法。因为以前的伺服系统闭环控制框图相对比较简单，采用面向过程的设计方法可清晰的表达控制框图中的对应关系。

下面示出了传统闭环控制运算中，陷波环节（二阶环节）的嵌入式C程序编写内容。

//陷波环节参数定义部分

//#define CurDifData_ CalCoeff 2.2019/*当前误差信号数据系数+/

//#define PrevDifData_ CalCoeff4.2328/*前一次误差信号数据系数+/

//#define PrevPrevDifData CalCoeff2.1164/*前两次误差信号数据系数*/

//#define PrevHYPData CalCoeff l.8575/*前一次闭环算法结果数据系数e/

//#define PrevPrevHYPData C alCoe ff0.9430/*前两次闭环算法结果数据系数*/

//陷波环节计算过程

g_stHistoryDifference [i].m_fCurData;

对于只有一个二阶计算节点的伺服系统闭环控制框图来说，该编写方法是比较合适的，如果在闭环控制框图中，二阶节点不只一个，并且在计算过程中还间插有一阶节点、多项式拟合等运算，这种面向过程的编写就显的有些乱，一旦总体要修改控制框图结构，程序调整起来工作量就比较大，并且很容易出现潜在错误。

3.2 改进的闭环运算程序设计方法

在闭环控制框图中，大致有“N阶节点”、“多项式拟合”和“3冗余表决”这三大类运算，如果把这三类运算分别进行模块化封装，使其自成一体、功能独立，则会大大简化闭环控制框图的嵌入式程序编写，软件的维护性也会有很大提高，便是总体临时决定改动闭环控制框图结构，程序的改动和传统方法相比，也会少很多，并且程序结构更加清晰，很难出现低级别的程序错误。下面分别介绍上述三大类运算改进的编写过程。

3.2.1 N阶节点

N阶节点的计算过程中，用到了前N次的输入/输出状态，为此，需要定义一些类似传统设计方法中的全局变量来保存这些状态，并且在每次运算时需逐次更新。为了简化闭环运算流程，采用了可面向结构的设计方法，把这些变量封装在结构里面，并由结构体对应的操作函数来执行运算。因每个节点的阶次和参数都不同，因此，便把它们作为了该操作函数的输入参数。这样，便可实现N节点的封装和独立运算。

下面示出了改进的闭环控制运算中，二阶陷波器的嵌入式C程序编写内容。

//N阶节点结构体封装（此处N<2），位于头文件中。

//……控制框图中基本运算节点结构体定义……

//控制框图中基本运算节点结构体定义

//控制算法框图中的每一个方框都看作一个控制节点，应该为每个方框都

//定义一个节点。节点中保存着该方框的输入和输出状态，默认为2阶系统。

//每个节点都带有积分输出保持开关标志和输出限位开关标志。

//该节点需要和对应函数ControlNode_Process（）配合使用。

struct ControlNode

{

//控制节点输入状态，降阶排列：O：当前状态X（K）1：前1状态X（k-l）2：前2状态X（k-2）…

float flnput[3];

//控制节点输出状态，降阶排列：O：当前状态Y（K）1：前1状态Y（k-l）2：前2状态Y（k-2）…

fioat fOutput[3];

//控制节点计算用分子参数降阶排列，和matlab离散化后数值与排列方式都相同

float fNum[3];

//控制节点计算用分母参数降阶排列，和matlab离散化后数值与排列方式都相同

fioat fDen[3];

//表示当前控制节点的阶数

int NodeOrder;

//输出保持开关1：使能输出保持，当前输出值保持为前一个状态值O：禁用输出保持

int Switch_OutputHold;

∥输出限位开关1：使能输出限位，当前输出值为最大限位值 O：禁用输出限位

int Switch_OutputLimit;

//节点输出最大值

fioat flvlaxOutput;

//节点输出最小值

fioat fMinOutput;

）;

extem

struct ControlNodestNode_Trap[2];

//陷波节点系数初始化，参数和matlab离散化计算值顺序相同，复制过来加逗号即可

float fXianbo_Coef_Num[3] ={0.5753，-1.0745， 0.5168）;

float fXianbo_Coef_Den[3]={1.0000，-1.7819， 0.7994};

//陷波节点初始化，陷波节点为2阶节点

InitiationNode（&stNode_Trap [i]，fXianboCoef_Num，fXianbo_Coef_Den，2）;

//閉环控制框图中的计算部分

//陷波节点计算mA

ControlNode_Process（&stNodeTrap[i]，fErrorResult_3）;

从改进后的程序中看出，在封装的结构体内还具有输出保持开关和限幅开关，如果当一个N阶环节为积分节点时，这两个开关就会有特殊的作用，通过控制这两个变量，便可自动实现积分开关和限幅的功能，而并不需要重新定义结构体。

N阶节点的分子和分母的离散化系数和matlab计算值排列顺序相同，只要复制过来，按C语言的语法添加逗号隔开即可。

3.2.2 多项式拟合

一个闭环控制框图中，会出现不同阶次的多项式拟合，改进的模块化设计中，提取多项式拟合的共同特征，把多项式系数和阶次作为多项式拟合函数的输入参数，从而实现了多项式拟合运算的封装。嵌入式程序的实现步骤如下所示。

//角位移反馈输入采样后拟合系数

//4阶拟合，系数排列顺序和matlab计算值相同

float fPolyCoefs_JiaoWeiYi[5]={0.00000146029， 0.0190893， 0.0000507086，＼

0.0000029009， 0.00000009069347）;

，/角位移传感器4阶拟合V.> Rad输入为电压，拟合后为弧度

fFeedbackjiaoWeiYiRad= Polyval（fPolyCoefsJiaoWeiYi，fFeedbackjiaoWeiYi_V，4）;

3.2.3 三冗余表决

三冗余表决的执行步骤比起N阶环节和多项式拟合要简单的多，改进后的模块化设计中，把三冗余表决运算封装成了函数。嵌入式程序的实现步骤如下。

//三冗余多数表决

fFeedbackjiaoWeiYi_Binary=

TripleRedundancyVote（giAcquisitionjiaoWeiYiData[i] [O]，

g_iAcquisitionjiaoWeiYiData[i] [1]，

g_iAcquisitionjiaoWeiYiData[i][2]）;

4 结论

在完全采用模块化设计方法后，伺服系统嵌入式控制软件的编写和调试时间缩短不少，因软件编写失误而导致的伺服系统开环事件大大减少，在提高效率节省资源的同时，也提高了伺服控制软件的可靠性。

伺服系统当前正向数字化转型，采用数字伺服控制器的型号越来越多，控制算法也越来越复杂，这种面向结构的模块化设计方法将越来越多地应用于各型号中。

参考文献

[1]苏奎峰，吕强，耿庆锋，陈圣俭编著.TMS320F2812原理与开发[M].电子工业出版社，2005.

[2]周航慈著，嵌入式系统软件设计中的常用算法[M].北京航空航天大学出版社.2010.