基于SSE的全局最优K-means算法

董炎焱

摘要 传统的K-means聚类算法对初值敏感，随机的初始聚类中心会造成簇的不稳定。本文采取全局搜索的方法避免了局部最优解，实验证明，采用SSE作为分类的标准，可以提高簇的稳定性。

[关键词]K-means聚类SSE 全局最优解 初始聚类中心

1 引言

聚类分析能够实现数据的归类，是数据挖掘的重要方法。K-means在聚类算法中的收敛速度较快，可以对数据进行预处理，产生数据的基本分布规律，但是传统的K-means算法中人为确定聚类数k，初始聚类中心的k个点随机选取，均影响到了聚类结果。本文针对k个聚类点的选取提出改进，增加K-means算法的稳定性。

2 K-means聚類算法

2.1 传统的K-means算法

设有数据点集{xu），xu是u维空间的一个点，u表示全部属性个数，人工设定聚类数为k：

（1）在{Xu}中任取k个初始聚类中心点，记为{wu}，k

（2）计算Xu和Wu的欧氏距离，归于最近的簇;

（3）更新聚类中心点，以各簇的均值代替原聚类中心点;

（4）重复（2）（3），直到连续两次聚类中心的距离小于或等于某阈值。

2.2 K-means的收敛测度SSE

聚类效果体现于聚类函数SSE的值，若SSE的值越小，认为聚类效果越好。设SSE=∑∑lI Xu-Wu || 2，对Wu求偏导数，并取为0，得到Wu=1/m∑Xu，m是以wu为聚类中心的点个数，1/m∑Xu就是SSE函数在wu类的最优解，每一次迭代，SSE将减小，最终趋于收敛。

2.3 传统K-means的局限性

聚类数人为确定，在大多数情况下，以人的先验知识不足以分清类别，要么k值偏小，忽略差别，要么k值偏大，过分强调类别，因此k值的选取需要多次的尝试，得到较为合理的聚类数。

SSE是非凸函数，由于初始聚类中心的选取是随机的，会形成局部最小值，不能保证是全局最小值，可多次更新初始聚类中心，重复算法，取其中最小的SSE。

3 全局最优解的K-means聚类算法

3.1 算法原理

设数据集点{xu}，k为聚类个数，{wu）为聚类中心点集：

（1）k=1，求解1/m∑Xu，其中m为数据点个数，得到第一个初始聚类中心wu1;

（2）k=2，将第一个聚类中心wu1分别与xul，xu2，Xu3，……xum进行K-means聚类，分别求出每次聚类的SSE.，找到min{SSEi），记录与之对应的第二个聚类中心wu2;

（3）k=3，将wu1、Wu2分别与xu1，Xu2，Xu3，……xum进行K-means聚类，记录与min{SSEi）对应的第三个聚类中心Wu3;

（4）依次类推，其中k

3.2 对比实验

实验数据来源为中华人民共和国统计局发布的“第六次人口普查”中“1—8各地区分性别、受教育程度的6岁及以上人口”的统计数据，选用该数据的原因是不考虑异常数据对实验的影响，取对数后进行聚类分析。

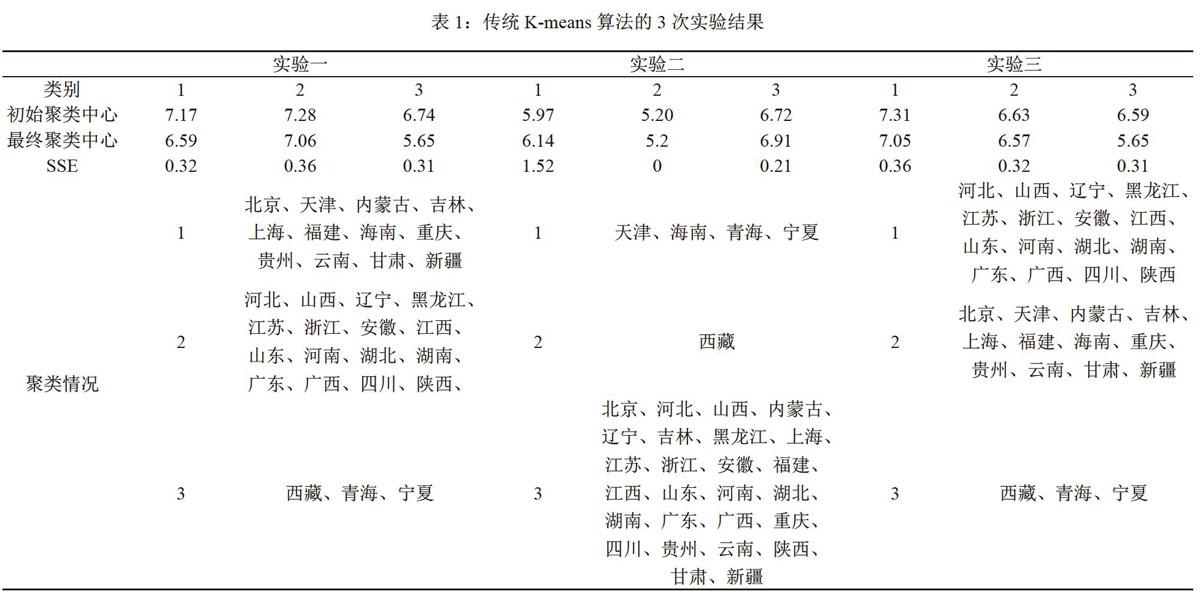
传统的K-means算法对初始聚类中心点随机选取，得到的聚类结果不稳定，设k=3，三次实验分别取不同的初始聚类中心，结果如表l。

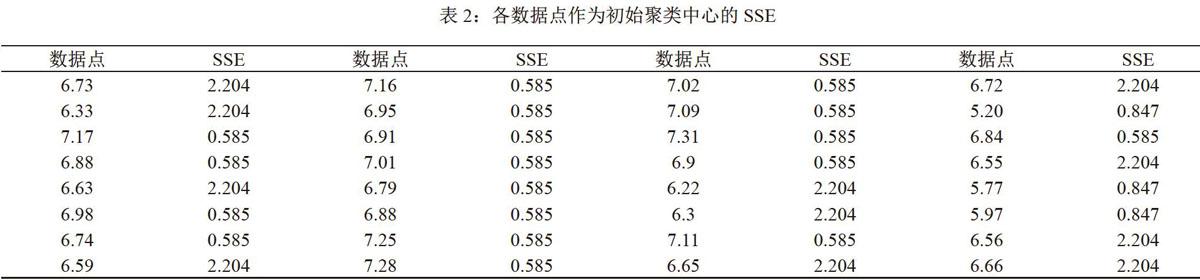
实验四为全局最优解的K-means聚类算法，第一个初始聚类中心是数据集的均值wul=6.73，数据集的每个点分别作为第二个初始聚类中心进行K-means聚类，得到SSE，如表2。

将表2的数值以图形表示，如图1。

3.3 实验分析

传统的K-means聚类算法对初始聚类中心选取敏感，造成簇的不稳定性。分析数据集{xu），x=6.73，σ=0.462，x±3σ的范围是（5.344，8.116），当数据点在这个范围内时，随机选择的初始聚类中心对聚类的稳定性影响小，否则会产生奇异的簇，如实验二。

实验四中如果按照全局最优解的理论算法，需要找到min{SSE），才能确定第二个聚类中心，但是通过数据点与SSE的图1就可以发现数据点己明显的分为三类，三个簇的SSE分别是0.585，0.847，2.204，数据点小于Wul，SSE就大。将SSE所对应的聚类中心作为初始聚类中心进行传统的K-means聚类，迭代5次后，最终的聚类中心是6.57，7.05，5.65，每个簇的SSE是0.32，0.36，0.31。实验四与实验一、三的最终聚类中心和SSE接近。

3.4 全局最优解的K-means聚类算法的改进

设数据集点{xu），k为聚类个数，{wu}为聚类中心点集：

（1）k=1，求解1/m∑Xu，其中m为数据点个数，得到第一个初始聚类中心wu1;

（2）将第一个聚类中心wul分别与wu1，Wu2，Wu3，……xum进行K-means聚类，分别求出每次聚类的SSEi，按照SSEi进行分类，相同SSE，的归为一簇;

（3）将不同簇的最终聚类中心作为初始聚类中心，进行K-means聚类，得到聚类结果。

4 结论

传统的K-means聚类高效而简单，应用范围广，但是随机的初始聚类中心和局部最优的存在影响了聚类的稳定性。本文从结合前人的研究成果对全局最优解的K-means聚类提出改进，缩短多次全局搜索的时间，增加聚类的稳定性。

参考文献

[1]谢娟英，蒋帅，王春霞，张琰，谢维信，一种改进的全局K-均值聚类算法[J].陕西师范大学学报（自然科学版），2010，38 （02）：18-22

[2]王晓东，张姣，薛红，基于蝙蝠算法的K均值聚类算法[J].吉林大学学报（信息科学版），2016，34 （06）：805-810.

[3]周世兵，徐振源，唐旭.新的K一均值算法最佳聚类数确定方法[J].计算机工程与应用，2010，46 （16）：27-31.

[4]Park H S，Jun C H.A simple and fastalgorithm for K-medoids clustering[J]. Expert SystemswithApplications，2009， 36 （02）： 3336-3341.

[5]王红睿，赵黎明，裴剑，均衡化的改进K均值聚类法[J].吉林大学学报（信息科学版），2006，24 （03）：172-176.