CT系统相关参数的标定和模板优化

付堉家 张津豪

摘要 CT （Computed Tomography）是一种可以在不破坏样品的情况下获取样品的内部结构信息的一种技术，目前在医学、考古学等领域有广泛应用。我们根据已知的吸收率反推几何模型时，利用MATLAB和radon变换绘制出图像，然后建立直角坐标系，将这两个图像相结合进行几何分析，建立模型I——几何分析模型。在射线垂直椭圆长轴入射、垂直短轴入射和射线穿过小球这三种情况下，分别计算探测器单元的间距，并对这些值取平均值得出探测器单元的间距为。利用托盘的中心和旋转中心在X轴和Y轴方向的偏差求出旋转中心的位置为。随后寻找出图像最宽和最窄处的角度为-90度和0度，进行逐步类推得出射线的转动范围。在已知未知介质的吸收信息的情况下，我们采用“滤波反投影法”建立模型Ⅱ

滤波反投影模型，并对滤波后的投影值进行内插，进行介质几何形状的确定。通过画出一个100*100的方框（正方形托盘）进行介质位置的确定。最后利用反投影得出十个位置处的吸收率。根据结果，由于物体内部含有大量孔洞，会产生大量吸收率过低的薄层。薄层的存在会使得投影图上少部分像素点缺失，从而导致反投影重建得到的原图产生丢失微小结构等后果。对于模型的改进问题，本文着重考虑影响CT系统参数标定的精度和稳定性的两个因素：椭圆长短轴测量次数少影响精度;噪声和射束硬化效应影响稳定性。因此，本文设计了一个由四个等大等间距椭圆和一个小圆组成的全新的标定模板以提高系统标定的精度和稳定性。

[关键词]CT系统 滤波反投影 灵敏度分析radon变换 图像处理

1 CT系统工作原理

X射线垂直于探测器平面平行入射，每个探测器单元看成一个接收点，且等距排列。X射线的发射器和探测器相对位置固定不变，整个发射.接收系统绕某固定的旋转中心旋转若干次。探测器上的等距单元测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到若干组接收信息并对物体进行分析。

2 模型的假设

（1）射线在空气中传播过程中不会衰减;

（2）在传播过程中不考虑干涉和衍射等光学问题;

（3）探測器旋转中心在旋转过程中不会发生偏移;

（4）光源不具有时间非均匀性和空间非均匀性。

3 模型的建立与求解

3.1 问题一的分析与求解

3.1.1 对问题的分析

我们利用MATLAB将附件一中的相关数据绘图，对数据利用MATLAB进行random变换处理，实现图像的重建和复原。

3.1.2 模型1：几何分析模型

模型的准备：

（1） CT成像原理的进一步分析。

有光学性质可知，当X射线穿过均匀材料的物质时，其强度的衰减率与强度本身成正比，即有：

射线穿过某物体时，（1）式中的μ并非常数，而是一个关于坐标平面（x，y）的函数μ（x，y），当射线沿平面内某直线L穿行时，当射线沿平面内某直线L穿行时，（2）式变为：

（2）利用Radon变换进行投影重建。

一个己知平面内沿不同直线对f（x，y）进行线积分，得到的像F（d，a）就是函数f的Radon变换。

一个己知平面内沿不同直线对f（x，y）进行线积分，得到的像F（d，a）就是函数f的Radon变换。

即：

平行束重建采用的是平移加旋转的扫描方式，如图1所示，射线源在某一角度下水平移动，将物体全部照射后旋转一角度，如此重复，在这个过程中探测器相应地运动以接收X射线。

平面中某一点密度可以看作是这一平面里所有经过该点射线的投影值之和。整幅重建图像可以看成是所有方向下的投影叠加而成。

因此有：

该式可当做反投影重建算法的计算。其中Xk表示像素k的值，Pk，表示经过像素k的第i条射线投影，np表示图像内的射线条数。

3.2 问题一的求解

以标定模板中的椭圆中心作原点，水平方向为x轴，竖直方向为y轴建系。

3.2.1 探测器单元之间的距离求解

（1）显然，光源和探测器绕着旋转中心旋转，当射线正好垂直标定模板的长轴入射时，此时被介质吸收的光源宽度最大，即图像的高度最大。

利用MATLAB对180个角度中不为O的个数N（吸收系数不为O，即穿过介质）进行计数，发现个数N最多为298或288（由系统误差引起），而椭圆实际长轴为L=80，所以探测器相邻单元之间的间距为：

（2）同理，当射线垂直于椭圆的短轴入射时，此时被介质吸收的光线的宽度最小，反映在图1中为180个角度中不为O的个数N（吸收系数不为O，即穿过介质）最小。

（3）小圆球在投影图中的体现为一条等距窄带，求出其对应的接收点个数N。

上述三种情况可得探测器单元间距。

3.2.2 CT系统旋转中心在托盘中的位置

我们知道CT旋转系统有其固定的旋转中心，以下称之为COR（Center of rotation）。理想状态是COR与托盘几何中心重合，在此情况下扫描可达最佳状态。而实际安装情况下往往因为种种外部因素，不能做到完全重合，因而存在一定的偏差。此偏差是影响成像质量的重要参数。

（1）首先我们考虑oo的情况。因为探测器有512个探测单元，因此该系统的旋转中心位于第256和257个探测器单元中间的位置。

（2） 900的情况。同理旋转中心纵坐标Y1与托盘中心纵坐标Yo的差值即为图中所示YC。

点（xc，YC）即为所求CT系统旋转中心与托盘中心的偏差。

由于探测器单元共有512个，其中间单元为256和257。现分别根据这两个进行计算：

3.2.3 X射线的180个方向

己知投影最窄出为0°方向，最宽处为-90°方向。其余的列数方案参照这两个度数一次类推。

值得注意的是，这里-90°和0°之间的间隔并非刚好90，而是92个，这也是因为系统存在一定的误差所致，详细的分析将在第4问的解答中体现。

3.3 问题二的分析与求解

3.3.1 模型的准备

（1）反投影重建。平面中某一点的密度可看作这一平面内所有经过该点的射线投影之和的均值。

即“反投影重建”计算式为：

Xk表示像素k的值，pk，i表示经过像素k的第j条射线投影，np表示图像内的射线条数。

（2）伪迹出现的原因。反投影的本质即取自有限物体空间的投影均匀地反投影到射线到达无限空间各点上，包括原先像素为零的点。

（3）滤波器作用。减弱或消除傅里叶变换的高频分量，从而减小噪声。经过查阅文献，为较完整保留目标图像的边缘，我们选用中值滤波进行去噪，可以用来减弱随机干扰和脉冲干扰。

3.3.2 模型的求解

因此在本题中，为了去除“伪迹”，我们采用“滤波反投影法（FBP）”进行本题的求解。

根据上问，我们己标定该CT系统参数，可以为具体测量做准备。在本问中，我们根据标定好的CT系统来求得物体的位置信息。

对每次测得的投影数据先进行一维傅立叶变换。据中心切片定理，将此变换结果看成二维频域中同样角度下过原点的直线上的值：

步骤5重复180次，完成全部反投影。

由于实际中物体是连续的，但是采样的投影数据是离散的，不一定能够正好落在采样点位置上，为了得到任意一点的值，需要对滤波后的投影值进行内插。

再根据matlab中自带滤波反投影函数iradon对投影数据进行反投影重建，再以旋转中心为正方形几何中心，画出一个100*100的方框。

3.4 问题四的求解与分析

3.4.1 问题的分析

如果计算每一次探测所得到的吸收率之和，在理想情况下吸收率总和应该为一个定值，但在問题（1）标定摸板中，吸收率总和是随探测次数而不断波动的，其中波动最大的位置在第130次-170次之间，除了噪声影响之外，这主要是射柬硬化效应造成的。CT中的x射线是具有频谱宽度的x线源，即x射线光子能量不同。在x射线穿过物体后，低能量部分易被吸收，高能部分较易穿过，因此在传播过程中，射线的平均能量会变高，即射线会“变硬”，称其为射束硬化效应。本题中，在第130～170次测量中，射线所需要透过的物体厚度最大，则此范围射线束较硬，导致所得吸收率误差较大，精度和稳定度降低。

3.4.2 问题的求解

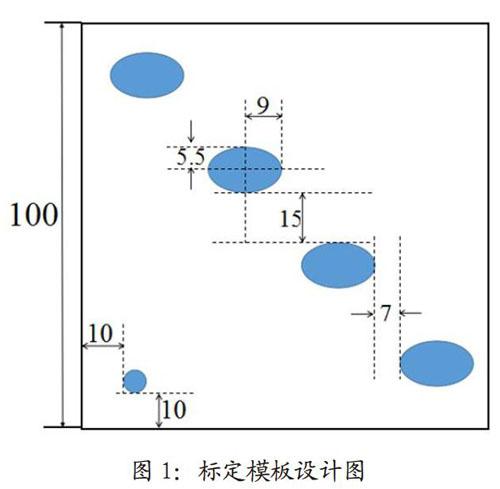
为解决上述问题，我们设计了如图1所示的标定模板。

该模板采用四个大小相等的椭圆，如图所示等距摆放在正方形托盘上，留足间距，保证X射线可以完整的照射到每个椭圆的长短轴。在左下角放置一个小圆形，用于确投影方向。相比于题目原来给定的一个椭圆和一个小圆的模板，该模板可以测量多次椭圆长短轴取均值，从而避免了单次测量的误差和损失，是标定更精确、更稳定。

4模型的评价和改进

4.1模型的优点

（1）在解决问题时，利用计算机软件进行计算较为方便，求解速度很快，工作效率高。

（2）在模型的推导中没有十分艰深的数学概念。理解方便，应用简单。

（3）模型可广泛应用于医学，考古等现实问题中，与实际问题紧密联系，通用性，推广性较强。

4.2 模型的缺点

在反Radon变换过程中，对滤波器选取，规避信号损失及其造成的尾影过程优化讨论不足。

4.3 模型的推广

系统优化和参数的标定在当前具有广泛的应用，因而本文所用的模型建立方法不仅适用于CT系统，还适用于其他在医疗、考古行业应用的大型设备。我国是一个大国，对于各种高档大型设备均具有很大的需求，所以从这个角度出发，本文提出的模型具有广阔的应用的前景。