基于强化学习的金融交易系统

傅聪 郝泳涛

摘要：强化学习（Reinforcement Learning）是解决序列化决策问题的途径之一，其在围棋、电子游戏、物理控制等确定环境下解决问题的能力已经得到证明。该文将强化学习应用到自动交易系统（Automated Trading System）的设计中，通过实验讨论了强化学习方法在混沌、动态环境下的表现，为自动交易系统的设计提出新的可能。不同于传统自动交易系统分别设计预测算法与策略算法的做法，基于强化学习的算法将两者合二为一，简化了设计步骤。该文第1章简述了强化学习发展现状;第2章阐述了金融交易问题的建模方法;第3章中通过实验，讨论了策略梯度算法与特征编码方式（RNN、CNN）在处理金融时序数据时的优劣。实验表明，使用RNN编码特征的方法有比较好的短期效果。最后，第4章总结了使用强化学习理论设计交易系统的优势与劣势。

关键词： 强化学习; 交易系统; 时间序列; 梯度下降

中图分类号：TP18        文献标识码：A        文章编号：1009-3044（2018）34-0172-04

1 引言

1.1 强化学习

随着AlphaGo[1]的成功，强化学习受到的关注日益增加，并被视为强人工智能的实现途径之一。作为机器学习的分支领域，强化学习基于Markov理论[2]，其思想是模拟智能体在与环境交互中学习的过程，非常适合处理序列化决策问题。

近年来，随着深度学习理论与硬件处理能力的发展，不少传统强化学习模型与深度学习理论相结合，使其能够处理的问题规模大大增加。例如经典的Q-Learning，在与神经网络结合之后，Deep Q Network算法（DQN）[3]在相当一部分Atari游戏中的表现超过了人类玩家。文献[4]证明了训练过程中最大化收益的过程就是沿着“策略梯度”优化参数的过程，基于这个理论的策略梯度算法在许多方面得到了成功应用。此外，与对抗网络（GAN）非常相似的演员-评论家（Actor-Critic）模型也是研究热点之一，该强化学习模型在学习过程中同时训练Actor与Critic两个网络，由Actor网络提出执行的动作，由Critic网络评估动作可能获得的收益，以此在交互过程中寻求最大收益。但是，由于AC模型的参数量的大，训练收敛速度不能得到保证，因此不少研究以加快AC模型的收敛速度为目标，例如文献[4]，提出了目标网络技术，提高训练稳定性与收敛速度。

除了基础理论与训练技巧，不少研究着重于使用强化学习解决实际问题。文献[5]使用AC模型，设计了水下机器人的自治控制算法;文献[6]研究了DQN在连续控制问题上的应用，为机器人连续控制问题提出了新的研究方向。强化学习在金融问题的应用也有一定的研究[7]阐述了强化学习主要算法应用到交易问题时需要做出的调整。文献[8]以DQN为基础，构造了Buy/Sell，Signal/Order 4个agent，设计交易系统，其在1999.1-2000.12的约30000个价格数据上训练，在2001.1-2005.12时间段内获得了最大约1138%的增长。

1.2 自动交易系统

交易过程可以看作一个序列化决策问题。在研究中，诸如股价、交易量等金融数据往往被研究者建模为时间序列，进而以统计分析、博弈论等方法为基础，分别设计自动交易系统的各个模块。交易系统的设计过程与各个模块如图1所示。据文献[9]所述，预测与决策是交易系统的两大主要组成部分，现有的研究大都只着眼于预测或者策略部分，少有将预测与交易策略结合在一起的研究。

本文将强化学习理论应用到交易系统的设计中，基于策略梯度算法设计了自动交易系统，并通过实验展示了交易系统的效果，同时比较了不同特征编码方式对于交易系统的影响，为交易系统的设计与研究提出新的可能。

3 实验

3.1 实验数据

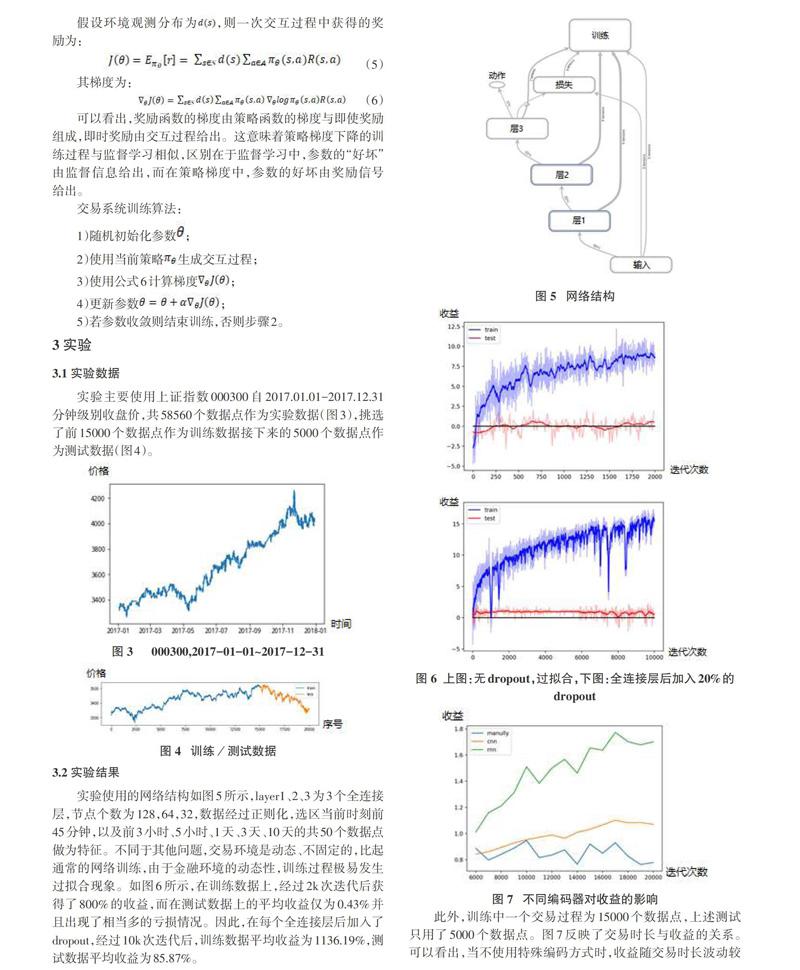
实验主要使用上证指数000300自2017.01.01-2017.12.31分钟级别收盘价，共58560个数据点作为实验数据（图3），挑选了前15000个数据点作为训练数据接下来的5000个数据点作为测试数据（图4）。

3.2 实验结果

实验使用的网络结构如图5所示，layer1、2、3为3个全连接层，节点个数为128，64，32，数据经过正则化，选区当前时刻前45分钟，以及前3小时、5小时、1天、3天、10天的共50个数据点做为特征。不同于其他问题，交易环境是动态、不固定的，比起通常的网络训练，由于金融环境的动态性，训练过程极易发生过拟合现象。如图6所示，在训练数据上，经过2k次迭代后获得了800%的收益，而在测试数据上的平均收益仅为0.43%并且出现了相当多的亏损情况。因此，在每个全连接层后加入了dropout，经过10k次迭代后，训练数据平均收益为1136.19%，测试数据平均收益为85.87%。

此外，训练中一个交易过程为15000个数据点，上述测试只用了5000个数据点。图7反映了交易时长与收益的关系。可以看出，当不使用特殊编码方式时，收益随交易时长波动较大，同时由于交易环境的不稳定性，随着时间偏差越大，收益越来越少。当使用CNN编码特征后，随着交易时长的增加，收益略微增加。并且由于其平滑了特征，波动较小。RNN編码特征的效果最好，虽然波动较大，但是其注重特征的近期变化，始终着眼于特征近期的变化，环境的不稳定性对于其影响较小，因此收益随时间的累计效应明显。

4 结论与展望

本文基于强化学习理论设计了自动交易系统，相比传统的交易系统设计，使用强化学习理论的优势在于简化了设计，免去了耦合预测、博弈算法的烦琐过程。此外，传统预测方法在预测价格时往往需要实时计算偏、正相关因数等统计学特征，以确定算法的参数（例如ARMA、GARCH等算法），计算量大，耗时严重。而前沿强化学习理论与深度学习结合紧密，使得使用RNN、CNN等各类特征编码器动态编码特征非常方便，减轻了人工设计特征的负担。

基于强化学习理论的交易系统也有不足，其缺陷主要分为以下两类：

一是由于强化学习还处在发展期，理论有待完善，能解决的问题也有限。比如当前后动作有逻辑依赖时难以定义状态-价值函数，比如在交易问题中，买入达到资金上限后，在卖出前不能买入;同理持有量为0时，不能做出卖出操作。本文同大部分研究者一样，将看涨、看平、看衰作为动作空间的定义，以此计算值函数与收益函数。有不少文献针对该问题进行研究，例如文献[11]，将三个动作作为特征，分别训练另外两个买入、卖出模型，使模型更加符合实际。

另一个难点在于金融环境的复杂与动态。不同时期的金融环境往往大不相同，没有一个模型能普世地在所有时期都能盈利。因此，如何将风险控制机制加入模型中也是研究的方向之一。

参考文献：

[1] Silver D， Huang A， Maddison C J， et al. Mastering the game of Go with deep neural networks and tree search.[J]. Nature， 2016， 529（7587）：484-489.

[2] Bradtke S J， Duff M O. Reinforcement learning methods for continuous-time Markov decision problems[C]// International Conference on Neural Information Processing Systems. MIT Press， 1994：393-400.

[3] Mnih V， Kavukcuoglu K， Silver D， et al. Human-level control through deep reinforcement learning.[J]. Nature， 2015， 518（7540）：529.

[4] Silver D， Lever G， Heess N， et al. Deterministic policy gradient algorithms[C]// International Conference on International Conference on Machine Learning. JMLR.org， 2014：387-395.

[5] Cui R， Yang C， Li Y， et al. Adaptive Neural Network Control of AUVs With Control Input Nonlinearities Using Reinforcement Learning[J]. IEEE Transactions on Systems Man & Cybernetics Systems， 2017， 47（6）：1019-1029.

[6] Zhao D， Zhu Y. MEC--a near-optimal online reinforcement learning algorithm for continuous deterministic systems[J]. IEEE Transactions on Neural Networks & Learning Systems， 2015， 26（2）：346-356.

[7] Eilers D， Dunis C L， Mettenheim H J V， et al. Intelligent trading of seasonal effects： A decision support algorithm based on reinforcement learning[J]. Decision Support Systems， 2014， 64（3）：100-108.

[8] Lee J W， Park J， Jangmin O， et al. A Multiagent Approach to Q-Learning for Daily Stock Trading[J]. IEEE Transactions on Systems， Man， and Cybernetics - Part A： Systems and Humans， 2007， 37（6）：864-877.

[9] Cavalcante R C， Brasileiro R C， Souza V L F， et al. Computational Intelligence and Financial Markets： A Survey and Future Directions[J]. Expert Systems with Applications， 2016， 55（C）：194-211.

[10] Du X， Zhai J， Lv K. Algorithm trading using q-learning and recurrent reinforcement learning[J]. positions， 2016， 1： 1.

[11] Lee J W， Park J， Jangmin O， et al. A Multiagent Approach to $ Q $-Learning for Daily Stock Trading[J]. IEEE Transactions on Systems， Man， and Cybernetics-Part A： Systems and Humans， 2007， 37（6）： 864-877.

【通聯编辑：唐一东】