基于Simulink的传染病模型仿真
2018-02-23石云凤,杨洪明,胡宇,张洪银,梁攀
石云凤,杨洪明,胡宇,张洪银,梁攀


摘 要:随着计算机的发展,数字仿真技术发展迅速且应用领域十分广泛。而传染病模型作为一类发展已十分成熟的数学模型,对其进行研究的相关文献数不胜数,传染病模型的实际应用也十分广泛,但很少有人将数字仿真技术应用于传染病模型。文章利用Simulink仿真软件对传统的SIR模型和在SIR模型中加入政府宣传防控效用的传染病模型进行仿真。首先建立传统SIR模型与在SIR模型中加入政府宣传防控工作效用的数学模型,然后针对这两类数学模型建立仿真系统,最后通过设置合适的参数值,得出仿真结果并与实际情况相对比,结果表明该仿真的结果与实际情况相吻合。
关键词:数字仿真;Simulink;SIR模型;宣传防控;过程仿真
中图分类号:TP391.9 文献标志码:A 文章编号:2095-2945(2018)06-0039-03
Abstract: With the development of computer, digital simulation technology develops rapidly and is widely used in many fields. As a very mature mathematical model, infectious disease model has been studied in numerous literatures, and the practical application of infectious disease model is also very extensive. But few people apply digital simulation technology to infectious disease model. In this paper, the Simulink simulation software is used to simulate the traditional SIR model and the infectious disease model which is added to the SIR model to promote the effectiveness of prevention and control. Firstly, the traditional SIR model and the mathematical model of the effectiveness of government propaganda and control are established in the SIR model, and then the simulation system is established for these two kinds of mathematical models. Finally, the appropriate parameters are set up. The simulation results are compared with the actual situation, and the results show that the simulation results are consistent with the actual situation.
Keywords: digital simulation; Simulink; SIR model; publicity and control; process simulation
引言
現代数字仿真技术是以相似原理、信息技术、系统技术及其应用领域有关的专业技术为基础,以计算机和各种物理效应设备为工具,利用系统模型对实际的或设想的系统进行试验研究的一种综合性技术[1]。与物理仿真技术相比,数字仿真不受被研究系统规模和结构复杂性的限制,以计算速度快、使用灵活、成本相对低廉等优势,成为分析、研究电力系统必不可少的工具,是系统仿真的重要研究方向[2]。随着计算机的发展,数字仿真技术取得突飞猛进的进步[3]。虽然数字仿真技术当前的应用领域很广,但是在该技术领域依然存在一些尚未攻克的技术难点,作为下一世纪重要技术竞争点,数字仿真技术需要人们给予更多的重视。
MATLAB中的一种可视化仿真工具Simulink,是一种基于MATLAB的框图设计环境,实现动态系统建模、仿真和分析的一个软件包,被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。Simulink软件在科学研究中应用十分广泛,它提供一个动态系统建模、仿真和综合分析的集成环境。在该环境中,无需大量书写程序,而只需要通过简单直观的鼠标操作,就可构造出复杂的系统。曾有人利用MATLAB中的Simulink仿真软件对无刷直流电机控制系统建模进行仿真[4],实现换热器稳态传热计算[5]。而传染病模型作为一类发展十分成熟的数学模型,相关的研究文献数不胜数。文献[6]刘玉英,肖燕妮等人研究了一类受媒体影响的传染病模型,文献[7]肖亚男研究了几类媒介传染病模型的稳定性。将传染病模型推广到实际应用中的文献也并不鲜见,例如赵剑华、万克文等人基于信息传播模型-SIR传染病模型研究了社交网络舆情传播动力学模型[8]。赵鹏飞,马民,谈依箴等作者曾基于SIR模型研究微信舆情传播[9]。王长峰,庄文英,于长钺等人基于改进SIR模型研究了的群体意见竞争演化[10]。虽然他们在研究过程中也有采用相关数学类软件进行问题分析,但利用数字仿真技术对传染病模型进行系统地仿真还较为鲜见。故本文首先建立传统的传染病模型——SIR模型,并建立在SIR模型中加入政府宣传防控工作效用的传染病模型,然后利用数字仿真技术对传染病模型进行系统地仿真,得到传染病传染过程的仿真结果,方便人们进一步对传染病的传染过程进行研究并推广到实际应用中。
1 传染病模型的建立
1.1 SIR传染病模型[9]
假设传染病考察区域的总人数为N,由于许多患者在传染病治愈后会对该病产生很强的免疫力,所以假设治愈者已经退出感染系统,故将人群分为健康者、病人和治愈者,则t时刻的这三类人群所占的比例分别为s(t)、i(t)、r(t),病人传染给健康者的传染率为?姿,日治愈率为?滋。设t=0时健康者、病人和治愈者所占比例分别为s0、i0、r0=0,于是便有微分方程的初值问题:
(1)
其中s(t)+i(t)+r(t)=1。
此传染病模型已是当前发展较为成熟的数学模型,也是比较传统典型的传染病微分方程模型,对传染病的传染过程能起到抽象描述作用。但在实际生活中,若突发传染病,政府为减少健康者染病的几率,会采取相应的宣传与防控措施。本文通过查阅相关资料[11],对传染病传染过程的仿真做进一步优化,建立了加入宣传防控工作的传染病模型。
1.2 加入宣传防控工作的传染病模型
在SIR传染病模型的基础上,加入政府的宣传防控工作效用,假设宣传防控工作的开展将使病人人数减少,减少的速度与传染病考察区域的总人数N成正比,其比例常数a取决于宣传防控的强度,故a也被称为宣传防控强度系数。设从t=t0>0开始做持续的宣传防控工作,于是便有微分方程的初值问题:
(2)
其中 称为Heaviside函数[12]。
此传染病模型在SIR模型的基础上加入宣传防控工作的效用,既考虑病人被治愈的情况,又考虑到政府的宣传防控工作,从而建立起更加符合实际情况的传染病模型,因而有助于本文对传染病的传染过程进行进一步的仿真,使得仿真结果更加真实可信。
2 仿真系统的建立
2.1 基于SIR模型的传染过程仿真系统
利用MATLAB软件中的Simulink仿真软件对SIR传染病模型进行仿真。此仿真系统通过人为设置日传染率a_1(即?姿)和日治愈率b(即?滋)的值、病人和健康者所占比例的初值,然后进行传染病传染过程的仿真,得到满足公式(1)所建立的SIR传染病模型,最终通过运行仿真系统得到基于SIR模型的传染病传染过程的仿真结果。总仿真系统图如图1。
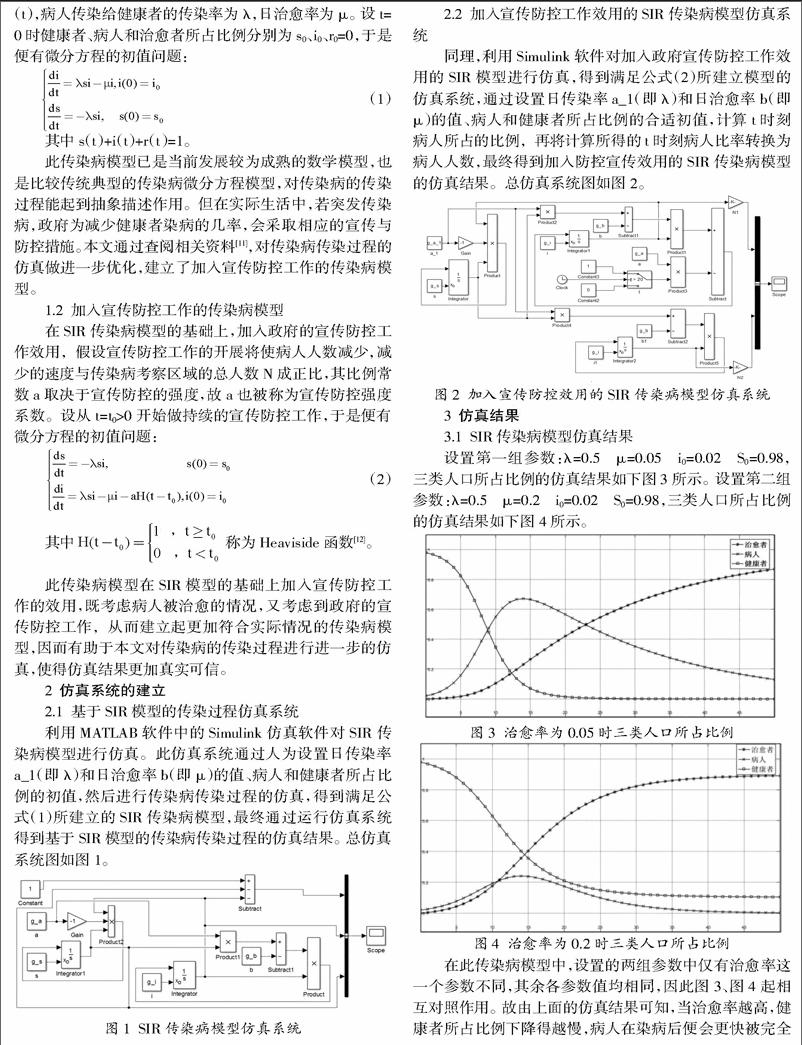
2.2 加入宣传防控工作效用的SIR传染病模型仿真系统
同理,利用Simulink软件对加入政府宣传防控工作效用的SIR模型进行仿真,得到满足公式(2)所建立模型的仿真系统,通过设置日传染率a_1(即?姿)和日治愈率b(即?滋)的值、病人和健康者所占比例的合适初值,计算t时刻病人所占的比例,再将计算所得的t时刻病人比率转换为病人人数,最终得到加入防控宣传效用的SIR传染病模型的仿真结果。总仿真系统图如图2。
3 仿真结果
3.1 SIR传染病模型仿真结果
设置第一组参数:?姿=0.5 ?滋=0.05 i0=0.02 S0=0.98,三类人口所占比例的仿真结果如下图3所示。设置第二组参数:?姿=0.5 ?滋=0.2 i0=0.02 S0=0.98,三类人口所占比例的仿真结果如下图4所示。
在此传染病模型中,设置的两组参数中仅有治愈率这一个参数不同,其余各参数值均相同,因此图3、图4起相互对照作用。故由上面的仿真结果可知,当治愈率越高,健康者所占比例下降得越慢,病人在染病后便会更快被完全治愈,成为治愈者。因此治愈者所占比例增加速率就越快,且当t→∞时,病人人数所占比例趋于0,符合现实生活中的实际情况,达到了对SIR传染病模型传染过程仿真的效果。
3.2 加入宣传防控的传染病模型仿真结果
设置参数:?姿=0.5 S0=0.98 ?滋=0.05 i0=0.02 a=0.2 t=20 N=10000,仿真结果如下图5所示。
在Heaviside函数中,本文设置在t=20时加入宣传和防控工作。按照Heaviside函数的定义[12],当0
在对传统的SIR传染病模型进行仿真时,设置了不同的治愈率,结果表明在治愈率高时病人人数比例下降速度明显高于治愈率低时的情况,该仿真结果符合实际,验证了仿真系统建立的正确性。在对加入宣传防控的传染病模型进行仿真时,本文设置了相同的治愈率,来对比加入了宣传防控工作效用与没有加入宣传防控效用时的传染病模型的病人人数变化趋势,从图5来看,加入宣传防控工作效用后病人人数明显下降,与实际结果吻合。
4 结束语
利用数字仿真技术直观、形象地反映传染病传染机制,从而对更好地理解传染病模型起到帮助作用。现代仿真技术不仅在传统的工程领域上应用广泛,而且正日益广泛地应用于如交通管理、环境治理、城市规划等领域,尤其对于制造业利用数字仿真技术具有更为重要的意义[3]。通过利用数字仿真技术对传染病模型进行仿真,掌握传染病模型的数学规律,可更加有利于对传染病的预防控制、经济行为以及其他社会实际问题提出实际建议。
参考文献:
[1]黄勇,孟庆鑫.浅谈仿真技术在军事领域内的应用[J].计算机与网络,2015,41(06):63-67.
[2]彭冲.电力系统数字仿真技术现状及展望[J].河北电力技术,2013,32(04):23-25+54.
[3]丁明瑞,施松新,周华民,等.基于数字仿真技术的家具产品的虚拟展示[J].机电工程技术,2014,43(12):183-185.
[4]纪志成,沈艳霞,姜建国.基于MATLAB无刷直流电机系统仿真建模的新方法[J].系统仿真学报,2003(12):1745-1749+1758.
[5]张泰岩,安连锁,刘树华.基于Simulink仿真实现换热器稳态传热计算[J].水利电力机械,2006(08):30-31+46.
[6]刘玉英,肖燕妮.一类受媒体影响的传染病模型的研究[J].应用数学和力学,2013,34(04):399-407.
[7]肖亚男.几类媒介传染病模型的稳定性分析[D].中北大学,2015.
[8]赵剑华,万克文.基于信息传播模型-SIR传染病模型的社交网络舆情传播动力学模型研究[J].情报科学,2017,35(12):34-38.
[9]赵鹏飞,马民,谈依箴.基于SIR模型的微信舆情传播研究[J].情报探索,2017(10):1-6.
[10]王长峰,庄文英,于长钺.基于改进SIR模型的群体意见竞争演化研究[J].情报杂志,2017,36(10):97-103+136.
[11]李汉龙,艾瑛,韩婷,等.Mathematica基础及其在数学建模中的应用[M].北京:国防工业出版社,2016:221-225.
[12]王海林,王吉民.Heaviside函数的Laplace变换建立超静定梁挠曲线方程[J].浙江科技学院学报,2012,24(06):466-469+487.
