标记平面立体线图的自适应遗传算法

熊思颖，董黎君



标记平面立体线图的自适应遗传算法

熊思颖，董黎君

(太原理工大学机械工程学院，山西 太原 030024)

针对由理查德·迈尔斯提出的标记线图的遗传算法进行改进：采取自适应参数调整法，同一代中适应度高于平均的个体杂交和变异率动态变化，适应度低于平均的个体杂交和变异率设为定值；在创建初始种群时加入了约束条件，旨在改善初始种群覆盖空间的不确定性和个体分布的相对不合理性；修正了遗传算法的适应度函数，使得以个体适应度为指标的选择算子能正确引导算法搜索解空间。用遗传算法标记6幅不同的线图，变量为杂交率、变异率公式中的参数和，分析算法标记成功率曲线的变化趋势，探讨算子参数设置对遗传算法性能的影响，结果表明属于区间[0，0.05]，属于区间[0.8，1.0]且为标记线图的遗传算法的最优参数设置。

线图标记；遗传算法；二进制编码；适应度

线图解释一直是计算机辅助设计和机器视觉研究的一个活跃领域，被广泛应用于建筑草图的处理和二维工程图的三维重建等方面。一致性标记问题由HARALICK和SHAPIRO[1]在20世纪70年代提出，起到排除线图的二义性和确定线图平面结构的作用，是三维流形物体重构的重要预备步骤。MYERS和HANCOCK[2]致力于研究多面体场景的线图的一致性标记，在此基础上，STANFILL和WALTA[3]提出了离散弛豫算法，表明使用一致性节点标记库便于在多面体对象的一致解释中指明搜索方向，通过分析三维场景及其二维投影之间的几何约束关系构造一致性节点标记库。文献[2]使用遗传算法确定线图棱线的最佳一致性标记，提出一种通过标记给出消失点的线图重建三维场景的方法，介绍了遗传算法是解决模糊线图标记问题的有效手段，证明基于种群和初始种群创建具有随机性特点的优化方法可以为线图标记问题提供优良的解。HANCOCK和KITTLER[4]将Faugeras和Hummel提出的贝叶斯框架应用于多面线框图的标记，BONNICI和CAMILLERI[5]将艺术线索如阴影和谱线与遗传算法结合的方法标记手绘图，文献[2]利用遗传算法的概率搜索和优化功能分配和评估线图的标记组合。

本文从杂交率和变异率、初始种群、适应度函数等方面着手改善由理查德·迈尔斯提出的标记线图的遗传算法易陷入局部最优和成功率低的缺点，验证改进后遗传算法的优越性，探讨标记线图的遗传算法的最优参数设置。

1 遗传算法设计

遗传算法的进化主要靠选择算子和杂交算子来推进，变异算子在算法的全局意义上只是起到修复和补充的作用[6]。传统遗传算法的杂交、变异率设为定值，在进化初期，固定的杂交、变异率能快速淘汰种群中性能低的个体，但是在进化后期，固定的杂交、变异率反而会破坏种群中的优质个体，放缓算法的收敛速度[7]。因此，在标记线图的遗传算法中引入自适应机制。

1.1 适应度函数

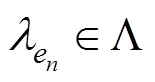
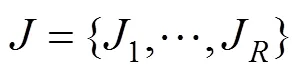
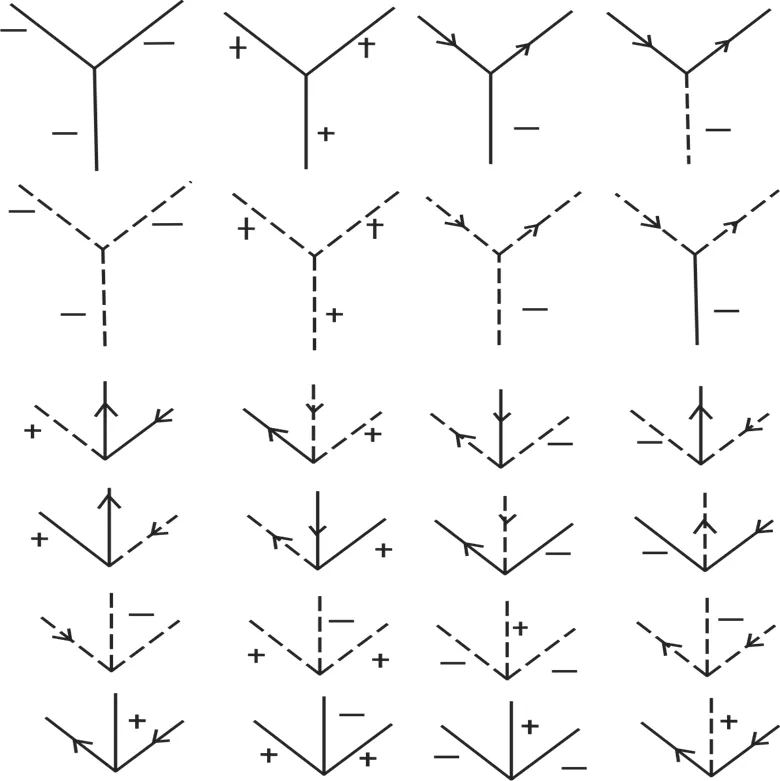
图1 24种合法的节点标记

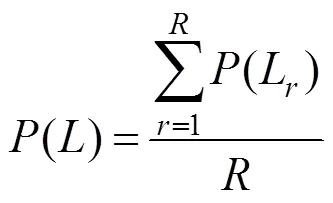
式(2)的待定参数是无记忆标记错误过程发生的概率。为了使汉明距离的指数作用更明确，可将式(2)改写为

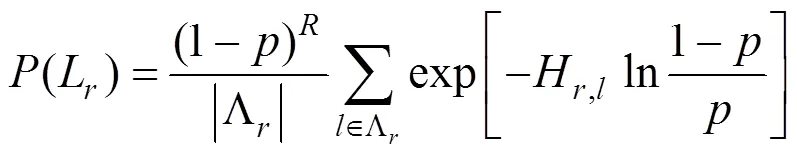
在多次运行遗传算法后发现，由理查德·迈尔斯提供的染色体适应度式(5)计算得出的染色体适应度过小，在选择操作中，某个个体的累计概率相对其之前个体突然变大，通常大于0.9，且其后个体的适应度变化非常缓慢，导致通过轮盘赌选出的个体适应度差异过小，甚至会出现种群中个体适应度相等的情况，导致优化无法进行，最终获得某个局部最优解。解决方案：引入与算法迭代次数相关的缩放参数，将其与式(5)中的价值函数C()相乘，新的适应度函数由式(6)~(8)表示，即

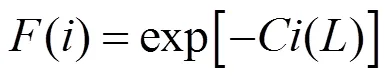
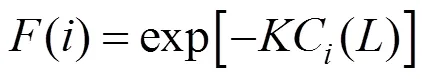
其中，C()为第个染色体的价值函数；()max为价值函数的最大值；为算法最大迭代次数；为算法的当前迭代次数；为一个随算法迭代次数非线性变化的正数。

1.2 染色体编码

线图标记算法将线图的棱边描述为凸棱(共有凸棱的两个面对于视点而言均为可见面，且位于棱线右侧的面逆时针转过一个大于90°、小于180°的角与位于棱线左侧的面重合，由记号“+”表示)、凹棱(共有凹棱的两个面对于视点而言均为可见面，且位于棱线右侧的面逆时针转过一个大于180°、小于270°的角与位于棱线左侧的面重合，由记号“–”表示)或遮挡棱(共有遮挡棱的两个面中只有一个面可见，由记号“→”或“←”表示，顺着箭头的方向走，被遮挡平面在左手边)。为标记一幅线图，需将线图表示为节点的集合，从预定义的节点库中为构成节点的每条棱线分配一个记号，节点库由该节点所属的某型节点的所有合法记号汇编而成。对于每一个节点，其节点库中包含多种记号样式，线图标记算法的任务是找出使得线图中所有节点被正确标记的棱线记号集合。

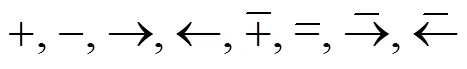
1.3 创建初始种群

本文采取文献[2]中建议的种群规模popusize=100。经典遗传算法的初始种群是随机产生的，初始种群在搜索空间的覆盖范围是不确定的，若初始种群空间不涉及全局最优解所在区域，而算子又不能在有限的进化代数内使种群个体分布覆盖到最优解区域，就不可避免地发生算法陷入局部最优解的问题，因此初始种群个体分布的相对合理性对于改善算法的全局收敛性至关重要。

代表一幅线图的染色体是由数个代表一个节点的基因片段拼接而成，结合24个合法的节点标记和在1.2节中叙述的染色体编码方法可以知道，每个棱线标记对应的字符的二进制表示中“1”的数目恒为3，每一条基因片段上的24个基因中“1”的个数恒为9个，因此可以在创建初始种群时约束染色体上“1”的数目，使得种群能够科学地表征解空间并且节约算法运行时间。

1.4 选择算子

选择算子的作用是利用某种策略在当前种群中选出优质的个体，增大其进入交配池的几率，以提高算法的全局收敛性，使算法具有良好的效率。

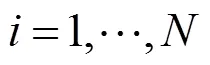
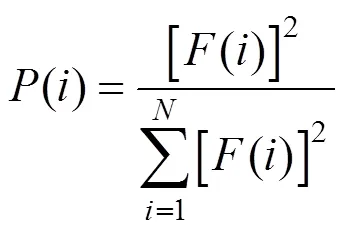
累计概率为

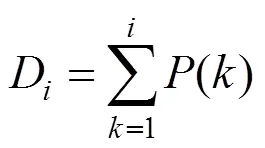
1.5 杂交和变异算子

破坏性杂交算子可以更好地探索搜索空间，因此本文采取均匀交叉。首先生成一个在0到1之间的随机数，如果杂交率P≥，则将随机配对的2条染色体上的基因互换，互换方式有别于点式杂交：随机生成一条与父代染色体长度相同的二进制位串，其中“0”表示不交换父代染色体对应位置上的基因，“1”则表示交换，称这条二进制位串为杂交掩码[10]。变异操作是按概率对染色体上随机选取的基因位取反，该操作对恢复种群的多样性有一定作用。首先产生一个在0到1之间的随机数，如果变异率P≥，则将变异算子作用于父代染色体，随机选取染色体上的变异位，变异位上的二进制代码是0则变为1，1则变为0。

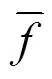
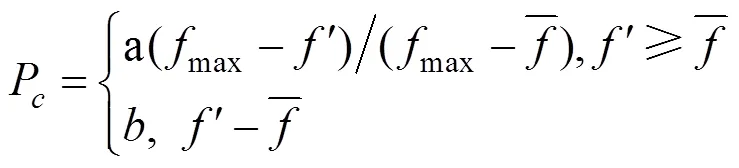
其中，a、b、c、d为小于等于1的常数。父代染色体经杂交变异操作获得子代染色体，比较父代染色体和子代染色体的适应度并将适应度低的一方淘汰，适应度高的一方进入交配池。首先应从适应度优于平均值的子种群popu1中每次随机取出2个要参与杂交的个体，重复populsize/2次，并将待杂交个体顺序放入杂交交配池中。

1.6 遗传算法流程图

遗传算法的基本流程如图2所示。终止条件：算法最大迭代次数=200。

图2 遗传算法流程图

1.7 判断算法标记成功的方法

根据编码规则，利用逆向思维对遗传算法最终迭代结果进行解码操作，码串中每长度为25的1个串经解码后可翻译为1个节点标记。每个节点由3条边组成，而每条边又可以作为另一个节点的1条边，也就是说每个节点都与3个面邻接，即将节点标记根据节点标记传播理论“粘”起来可以形成一个封闭的“标记环”，且每个节点属于3个“标记环”。将上述“标记环”与所标记的线图进行匹配，匹配成功则表示算法标记成功，反之，则失败。

1.8 改进后的遗传算法的优越性

选取图3所示的线图作为实验对象比较改进后遗传算法(improved genetic algorithm，IGA)和理查德提出的标记线图的遗传算法(genetic algorithm proposed by Richard，RGA)的收敛速度和稳定性。RGA算法随机生成初始种群，种群大小取100，选择操作为一般轮盘赌法，采用多点交叉和基本位变异，杂交率取0.9，变异率取0.03；IGA算法中a取1，b取0.6，c取0.1，d取0.05。不限制算法的迭代次数，两种算法各执行50次，记录算法成功率、获得正确标记所需的平均迭代次数，结果见表1。

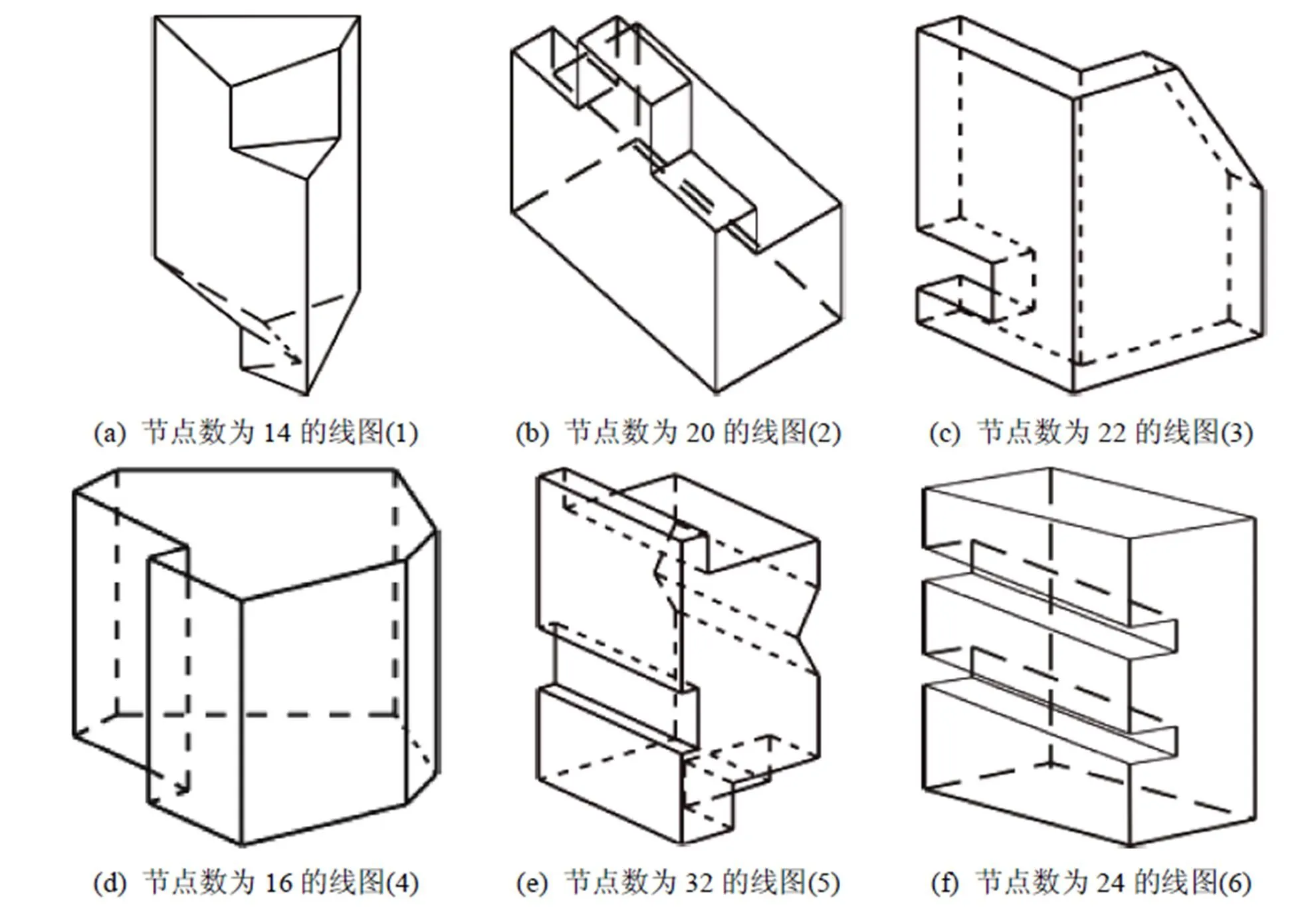
图3 实验线图

表1 两种算法实验结果比较

从表1的数据可以看出，RGA算法的成功率在30%左右，且收敛的代数偏大。IGA算法的成功率在58%左右，收敛代数明显降低，改进后遗传算法的稳定性和收敛速度相较于标准遗传算法均有较大提升。

2 实验设计

实验用的测试线图如图3所示，标记后的线图如图4所示。遗传算法用MATLAB R2012b编写。统计遗传算法成功标记线图的次数并计算其占总实验次数的比例(平均值)，绘制成折线图，分析折线走势探讨遗传算法的最佳参数设置，讨论杂交率和变异率的选取对算法性能的影响。常数b和d是针对适应度小于平均值的个体设置的杂交率和变异率，沿用RGA算法b取0.6，d取0.05。如果将实验变量、的取值编码为－、－，上述希腊字母分别代表参数、的具体数值(表2)。设定参数为定值时研究参数取不同值时的成功率，表3的9个横行代表代号为i~ix的9组实验，每组实验有9个不同的参数设置，每个参数设置对应的遗传算法均运行50次，每次迭代200代，根据运行结果计算每个参数设置对应的算法成功标记线图的概率，计算出每组实验的平均成功率，反映在图5折线的纵坐标上；设定参数为定值时研究参数取不同值时算法标记成功的概率，表3的9个纵列代表代号为I~IX的9组实验，按照上述方法绘制图6。

图4 标记后的线图

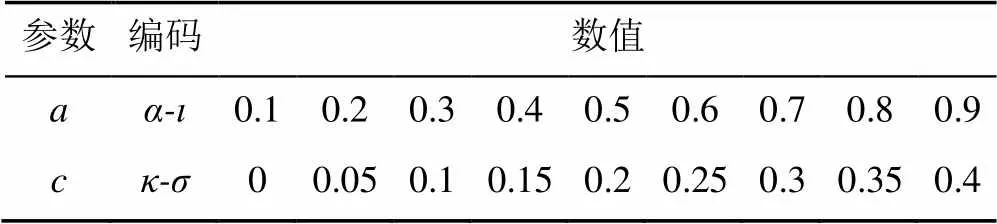
表2 参数a、c的取值

表3 18组实验参数设置

图5 参数c对算法成功率的影响

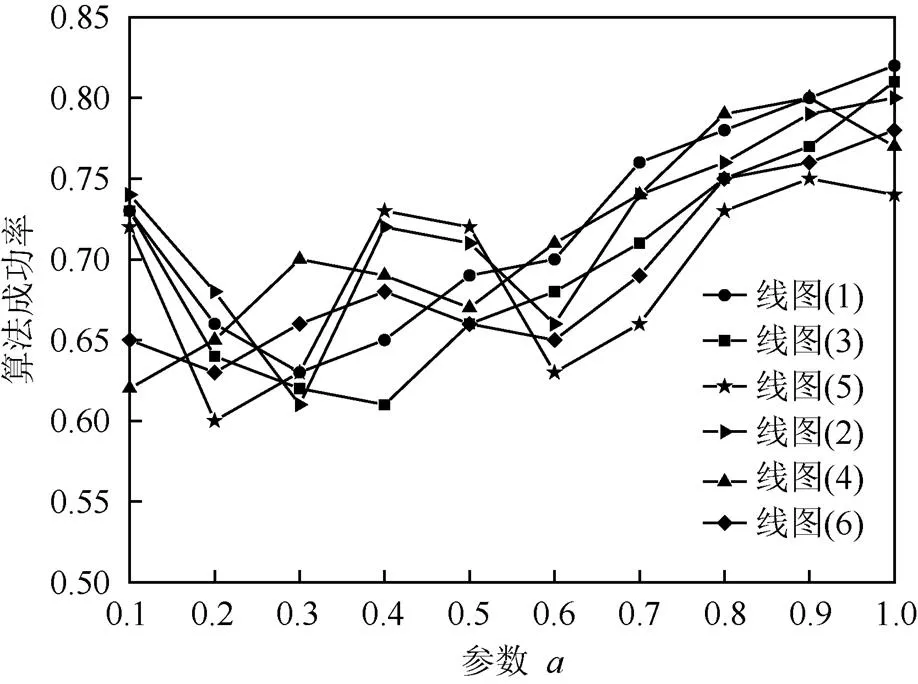
图6 参数a对算法成功率的影响

3 实验结果

由图5可知，参数的变化对算法成功率的影响颇为显著。当大于0.2时，6幅线图标记成功的概率除了线图(4)有小幅上升外均大幅下降，且当大于0.35时，成功率基本上不足50%；当位于区间[0，0.05]时，算法成功标记线图的概率较高，对于线图(1)、(2)、(5)，算法成功率在取0.05时达到峰值，虽然在此区间内线图(3)、(4)和(6)标记成功的概率呈下降趋势，但就整体变化而言，下降趋势相对较缓，且概率下降小于10%；当位于区间[0.05，0.20]时，线图(1)、(2)、(4)的成功率曲线均呈现不同程度的直线下降趋势，线图(3)、(4)、(6)的成功率曲线有所波动，但相比于区间[0，0.05]成功率是有所下降的。参数的选取直接影响种群中适应度相对较高个体的变异率，且与变异率是正比关系，因此在选取参数时，最好不要在大于0.1的区间内选取。实际上，小但非零变异率是种群进化的重要手段，但不是算法最终收敛的关键因素。

分析图6，随着参数的变化，线图成功率曲线波动较大，当在某些小区间上增大时，成功率上升到某个上限便会有所下降，在区间[0.8，1.0]时曲线变化相对缓和且此时算法的成功率较高。参数的取值对应种群中较优秀个体的杂交率，且二者是正比关系。

综上所述，参数属于区间[0，0.05]且参数属于区间[0.8，1.0]时为标记线图的遗传算法的最优参数设置。

4 结束语

遗传算法虽然是一种广泛应用的全局搜索算法，但仍然存在许多不足，比如容易发生过早收敛、收敛速度慢、陷入局部最优等问题。通常可以将遗传算法与具有较强局部搜索能力的启发式算法如爬山法、梯度法等结合起来，在一定程度上改进遗传算法的性能。

二进制编码的长度与线图的节点数成正比。用遗传算法标记复杂线图时，由于这类线图包含数量可观的节点，普遍存在编码串过长的问题，算法的计算精度虽有提高，但由于算法的搜索空间急剧扩大，计算量增加，导致算法的效率变差，同时会削弱变异算子对染色体的作用。可以尝试从以下两个方面改进上述缺点：直接方法是换一种编码策略，可以采取浮点数编码，用在算法搜索空间较大的情形，便于将遗传算法和经典的优化算法结合使用；间接方法就是从线图着手，先将复杂线图划分为若干简单线图，对简单线图进行标记后再将其依据标记的一致性或标记的传播理论“粘合”起来。

上述只探讨了平面立体完整线图的标记情况，对于不完整的线图，可以将线图补全后再用改进后的遗传算法标记。亦可以将上述方法根据曲面的标记特点运用于曲面立体线图的标记。

[1] HARALICK R M, SHAPIRO L G. The consistent labeling problem: Part I [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 173-184.

[2] MYERS R, HANCOCK E R. Genetic algorithms for ambiguous labeling problem [J]. Pattern Recognition, 2000, 33(4): 685-704.

[3] STANFILL C, WALTA D. Toward memory-based reasoning [J]. Communications of the ACM, 1986, 29(12): 1213-1228.

[4] HANCOCK E R, KITTLER J. Edge-labeling using dictionary-based relaxation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(2): 165-181.

[5] BONNICI A, CAMILLERI K P. A constrained genetic algorithm for line labeling of line drawings with shadows and table-lines [J]. Computers & Graphics, 2013, 37(5): 302-315.

[6] 李雅, 黄少滨, 李艳梅, 等. 基于遗传算法的反例理解[J]. 哈尔滨工程大学学报, 2016, 37(10): 1394-1399.

[7] 曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究[J]. 计算机应用研究, 2015, 32(11): 3222-3225.

[8] GAO M T, CAI X P. Labeling line drawings with hidden-part-drawn of planar object with trihedral vertices [J]. Computer Aided Drafting, Design and Manufacturing, 2015, 25(2): 1-13.

[9] BURKS A R, PUNCH W F. An analysis of the genetic marker diversity algorithm for genetic programming [J]. Genetic Programming and Evolvable Machines, 2017, 18(2): 213-245.

[10] LATIF A H M M, BRUNNER E. A genetic algorithm for designing microarray experiments [J]. Computational Statistics, 2016, 31(2): 409-424.

[11] LI H Y, ZUO H F, LIANG K, et al. Optimizing combination of aircraft maintenance tasks by adaptive genetic algorithm based on cluster search [J]. Journal of Systems Engineering and Electronics, 2016, 27(1): 140-156.

A Self-Adaptive Genetic Algorithm for Labeling Line Drawings of Planar Objects

XIONG Siying, DONG Lijun

(College of Mechanical Engineering, Taiyuan University of Technology, Taiyuan Shanxi 030024, China)

This paper improves the genetic algorithm for labeling line drawings presented by Richard Myers in the following areas: self-adaption parameter adjustment method was used, the hybridization rate and mutation rate of individuals with high fitness in the same generation were dynamically changed, and the rate of hybridization and mutation of individuals with lower fitness was set as a fixed value; the constraints were established when the initial population was created, with the aim of improving the uncertainty of the initial population coverage space and the relative irrationality of the individual distribution; the fitness function of the genetic algorithm was modified so that the selection operator with the individual fitness as the index could correctly guide the algorithm to search the solution space. The genetic algorithm was employed to mark six different line drawings, the parameterandin the formula of hybridization rate and mutation rate were used as experimental variables, the change tendency of the algorithm’s mark success rate curve was analyzed, and the influence of operator parameter setting on the performance of genetic algorithm was discussed. The results show thatbelongs to interval [0, 0.05] andbelongs to interval [0.8, 1.0] andis the optimal parameter setting of the genetic algorithm for labeling line drawings.

line drawing label; genetic algorithm; binary coding; fitness

TP391.41

10.11996/JG.j.2095-302X.2018061105

A

2095-302X(2018)06-1105-07

2018-03-15；

2018-03-28

熊思颖(1993-)，女，江西九江人，硕士研究生。主要研究方向为计算机图形学。E-mail：1140980289@qq.com

董黎君(1962-)，女，山西运城人，教授，博士，硕士生导师。主要研究方向为计算机图形学、图学理论及应用。E-mail：dlj_lmq@163.com