桥梁应变监测数据中的温度效应分析

杨海红

（山西交通控股集团有限公司 运城南高速公路分公司，山西 运城 044000）

1 概述

桥梁健康监测中应变监测是最重要的监测内容，但由于桥梁结构受到复杂的温度场影响，导致实测应变数据受温度影响呈现较明显的波动。事实上，桥梁结构除了受到车辆荷载作用之外，温度也是较为重要的环境激励。近年来，已有学者针对实测数据采用滤波的方法提取缓慢变化的温度周期趋势，从而将车辆荷载与温度效应分离，为结构后续的安全监测及状态评估提供参考。

但是针对温度周期趋势的研究仍有不足，由于车辆荷载对结构的运营的安全有着重要的影响，人们重点关注的是车辆荷载效应，而忽视了温度效应。实际上结构实测应变的变化趋势很大程度上与温度有关，因此有必要对温度效应进行深入研究。

本文依托风陵渡黄河大桥健康监测，该桥上部结构为预应变变截面连续梁，由主孔桥和边孔桥组成。主孔桥跨径组成为（87+7×114+87）m，边孔桥跨径组成为5×87 m。选择主孔桥第13跨跨中下缘应变及相应的温度测点。

2 实测应变的变化规律

风陵渡黄河大桥健康监测系统自2010年运行至今已将近8年，积累了大量的实测数据。虽然传感器已经进行了温度系数标定，但由于桥梁现场与实验室的环境存在着很大的不同，因此，采用多年的实测应变和温度数据进行回归分析，并在此基础上对应变传感器进行温度修正，尽量剔除温度的影响。

应变监测的采样频率为3 min采集一次，由此造成全年的数据非常庞大，每个传感器全年有17万多条数据，由此使得后期处理相对较难。通过对数据进行认真分析,每天应变数据是随着日照温差的波动而周期变化，清晨是一天中箱梁内外温差最小的时段。因此选择每天清晨5：00时刻的应变测试数据进行分析。首先提取每天5：00～6：00范围内实测数据，取其平均值作为当天应变及温度测试结果代表值。通过绘制应变温度曲线图，发现其与温度之间具有较好的线性相关，经回归分析，可决系数R2接近于1，温度与应变回归分析见图1。

图1 应变温度回归分析

在进行回归分析过程中，应变和温度均换算为相对变化量，回归方程中的截距也相应为零，便可得到应变温度的回归系数。按照上述方法对历年的监测数据进行回归分析，结果如表1所示。

表1 历年温度回归系数表

从表1可看出，历年温度回归系数偏差不大，可决系数均接近于1，采用历年回归系数的平均值对实测应变进行温度修正，修正后的2018年8月实测曲线见图2。

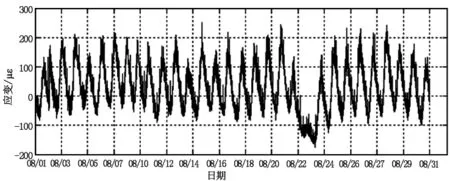
图2 2018年8月实测应变曲线图

从图2可以看出，虽然采用历年的温度回归系数对实测应变进行了温度修正，但应变实测曲线仍然每天随温度产生较大的波动。应变曲线中存在着大量的毛刺，而这些毛刺是由车辆荷载产生的[1]。

由此，本文针对实测应变数据的变化规律，结合相应的温度测试结果，对实测数据中的温度效应进行分析。

3 实测应变的温度效应分析

3.1 实测应变的平滑处理

从图2可看出，实测应变受车辆荷载影响曲线并不光滑，因此，首先采用小波分析的方法将车辆荷载分离出来，从而得出光滑的仅受温度影响的应变曲线见图3。

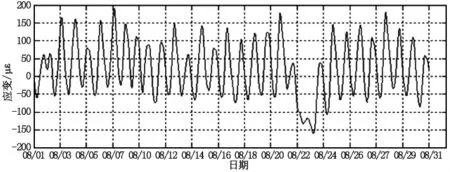
图3 小波分析后的应变曲线图

3.2 温度滞后的处理

对温度测试数据进行分析，温度变化曲线如图4所示。

图4 温度变化曲线图

对比图3与图4可以看出，应变与温度变化规律基本一致，二者存在明显的相关关系，同时相对应变而言，实测温度有一定的滞后，这是由于测试的为箱内温度，相对密封的箱梁结构导致箱内温度与大气温度进行热交换慢于结构的导热过程。在数据处理过程中，对温度数据进行平移，从而建立二者的真正对应关系。

3.3 多段温度回归模型

经上述分析之后，直接对温度与应变进行回归分析，结果发现二者完全没有相关关系，曲线拟合较差。考虑到二者曲线形态较相近，因此，将曲线进行分段，分别进行温度回归[2]。首先根据曲线变化规律，寻找相应的特征点，采用特征点将曲线分隔为若干段，总共划分57段曲线，对每段曲线进行回归分析。

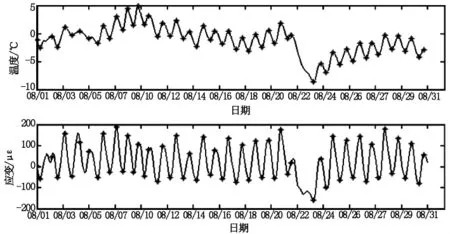
图5 利用曲线特征点进行分段

通过对每段曲线进行回归分析，仅有两段曲线的可决系数在0.5～0.6之间，其余所有曲线的可决系数在0.89～0.99之间，说明二者具有较好的拟合优度。图6为其中一段曲线的拟合结果。

图6 应变温度回归分析

从分段曲线来看，应变与温度之间有着较强的线性回归关系，但当总体进行回归却没有这种规律，说明每段曲线其相应的回归系数各不相同。为了能够总体把握温度与应变的相互关系，需要对每段曲线的回归系数进行分析，寻找其相应的规律，选择每段温度的平均值、相对值（最大值与最小值的差值）作为自变量，每段曲线的回归系数作为因变量进行回归分析。

经多次组合分析，发现截距（即拟合公式中的b）与平均值之间有着较强的线性关系，而温度系数（即拟合公式中的a）与相对值之间存在一定的指数关系，回归分析见图7和图8。

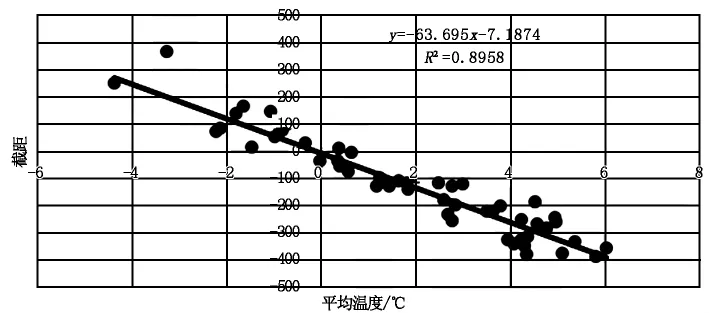
图7 截距与平均温度的回归分析

图8 斜率与温差的回归分析

3.4 利用温度回归公式进行应变预测

采用上述方法便可得到温度与应变回归的一般公式为：

式中：Si为某时刻的应变；Ti为当前时刻的温度；T1为当前温度段的最大温差；T2为当前温度段的平均温度；a1、b1、a2、b2分别为回归系数。

按照上述方法对温度进行分段平移之后，便可按照式（1）进行计算。然而在每段的分割点处，由于该点两侧的回归公式计算结果不同，导致在该点出现台阶式的突变。导致曲线不连续，为了解决这个问题，经多次调整试算，采用以下办法对计算应变进行修正：

a）首先分别根据该点两侧回归公式的置信区间计算相应的置信度。

b）如果两侧的置信度较为接近，则该点的应变值为两侧计算结果的平均值，并以此结果对该点两侧的回归公式进行修正，重新计算这两段的应变值。

c）如果两侧的置信度相差较大，则选用置信度较大一侧的计算结果作为该点的应变值，并以此为依据对置信度较小一侧的计算结果进行修正。

按照上述方法计算结果见图9，计算残差均值为5.38με，说明多段回归是能够满足工程实际需要的。

图9 修正后的应变计算结果

4 结论

a）应变与温度之间存在着线性相关关系，但不同时间段内，二者的相关系数不同，采用分段的温度回归模型能够获得较好的拟合优度。

b）每段应变回归模型中，曲线斜率与该段时间的温差存在相关关系，若采用线性回归时，温差较大时会导致出现负值，而采用指数拟合，温差越大其变化率也相应较慢，更符合实际情况。

c）每段曲线的截距与该段时间的平均温度存在较强的线性负相关。

d）应变与温度的多段回归模型也可应用于主梁挠度等其他参数，可在此基础上对桥梁进行荷载识别与安全评估。