转子偏心对U型单相永磁同步电机的影响

付敏 于静 张晗 沈镭

摘 要：为了研究转子偏心对U型单相永磁同步电机性能的影响，采用有限元法分析了电机内的电磁场，在虚位移法和麦克斯韦应力法的基础上，计算了当转子分别发生静态偏心和动态偏心时，电磁转矩的变化量以及定子侧所受到的径、切向电磁力。并通过傅里叶分解，研究了转子偏心对电磁力波阶次和频次的影响。计算结果表明，转子偏心引起电机内电磁场不对称分布，且气隙磁密幅值随偏心距离的增加而增大;不同偏心状态对电磁转矩波动有不同的影响;偏心导致电磁力波奇次谐波分量大幅度增加。

关键词：单相永磁电机;有限元法;转子偏心;电磁力

DOI：10.15938/j.jhust.2018.06.012

中图分类号： TM351

文献标志码： A

文章编号： 1007-2683（2018）06-0062-08

Abstract：In order to analyze the impact of rotor eccentricity to the performance of u-shaped single-phase permanent magnet synchronous motor the finite element method is adopted to analyze the electromagnetic field inside the motor. On the basis of the virtual work method and the Maxwell stress tensor method the variation of electromagnetic torque radial and tangential electromagnetic force densities in stator side were calculated when static eccentric and dynamic eccentric occurred in rotor. Then the influences of rotor eccentricity on the electromagnetic force order and frequency were studied through the Fourier decompose. The calculation results indicate that asymmetrical distribution of electromagnetic field in the electric machine due to rotor eccentricity and the air gap flux density amplitude increases with the increases of the eccentric distance; different eccentric states have different effects on the electromagnetic torque volatility; eccentric results in a substantial increase of electromagnetic force odd harmonic component.

Keywords：single-phase permanent magnet synchronous motor; finite element method ; rotor eccentricity; magnetic force

0 引 言

U型单相永磁同步电机目前越来越多的应用于人们的日常生活，特别是在小功率的家用电器中广泛应用。U型永磁同步电机以其结构简单、高效节能和使用寿命长等优点被大规模加工生产，并且在微特电机制造行业中具有很大的成本优势[1]。

目前对该电机的研究主要集中在该电机的运行原理、起动问题的研究。文[1]分析了阶梯气隙结构对电机内部磁场、定位转矩以及转子初始位置角的影响，得到最优气隙参数，优化该电机的起动性能。文[2]基于二维有限元法对该电机绕组电感、磁链和定位转矩进行了计算，同时讨论了电源合闸角、转子初始相角、磁链和负载转矩对电机转速和旋转方向的影响。文[3]阐述了U型单相永磁同步电机的自起动原理，并通過Matlab仿真以及实验具体分析了该电机气隙结构、气隙半径以及极弧包角对定位转矩以及定位角度的影响。文[4]提出了一种新型结构的U 型单相自起动永磁同步电机，在原电机转子外侧增加1 个铜质套筒，该铜套起到抑制转速波动、降低振动的作用，同时提高了电机带载起动的能力。文[5]通过Workbench和LMS Virtual.Lab对 U 型单相永磁同步电机进行联合仿真，获取声压在空间的分布和声压频响特性。得出电机在运转时定子侧发生较大的振动位移、振动速度以及加速度，导致电机结构的金属疲劳，从而极大的影响了该电机的使用寿命。

在电机应用过程中会出现一些故障，其中转子偏心是最常见的电机故障之一[6-8]。转子偏心是由于在电机生产过程中受到加工装配工艺的限制、转子刚度不足以及运行中轴承磨损等原因导致。从而造成定、转子间气隙不均匀，气隙磁场发生畸变，加重了电机的振动和噪声[9-11]。由上述可知转子偏心影响电机的运行，但关于转子偏心对该电机影响的文献还未见到。

本文基于有限元法对U型单相自起动永磁同步电机进行仿真计算，得到转子发生偏心故障时的磁场分布、在此基础上采用虚位移法和麦克斯韦应力法分析偏心对电磁转矩及定子所受电磁力的影响。

1 电机数学模型的建立

1.1 U型单相永磁同步电机的结构

U型单相永磁同步电机结构如图1所示，转子由两个铁氧体材料制成的半圆柱组成，定子铁芯由U型硅钢片叠压制成，同时为了实现电机自启动，定子铁芯内径采用三段半径不同的同心圆弧连接的结构，该电机的特殊结构使得不同位置的气隙大小不相等，其中气隙最大为1.1mm，气隙最小为0.5mm。由于气隙不对称使得转子的初始相位角θ≠0[1]。考虑到该电机转轴直径较小，对电机的磁场和启动性能影响不大，所以该电机在仿真中可将转子按实芯永磁圆柱体处理。

1.2 磁场有限元计算

1.2.1 电磁场的计算

利用有限元法对该电机进行磁场分析时，为了简化分析，作如下假设：1）不考虑磁場在轴向上的变化;2）忽略位移电流及其影响;3）取电机外边界5cm处定义为计算区域的外边界，并令其满足第一类边界条件。于是得到U型单相永磁同步电机电磁场方程[12-13]：

基于有限元法计算该电机在空载状态下达到稳定运行时（0.4s～1s）的定子电流随时间变化曲线如图2所示。为了验证该电机仿真模型的正确性以及计算结果的可靠性，对电机进行空载运行实验，得到定子电流随时间变化曲线如图3所示。

结合图2和图3可以看出，仿真计算结果与电机测试结果基本一致，说明利用本文计算方法所得到的计算结果具有可靠性。

1.2.2 电磁转矩的计算

由于麦克斯韦应力法和虚位移法在计算电磁转矩时，仅需用到各单元的磁通密度和磁场强度，所以适用于各种电机不同运行方式的转矩计算。

麦克斯韦应力法是将Tm表示为转子气隙内一个闭合曲面S的积分。虚位移法是采用差分代替偏微分的方法，通过计算虚位移发生前、后的磁场能或磁共能的变化来确定电磁转矩。本文采用虚位移法计算电磁转矩，求得电磁转矩公式为[14]：

1.2.3 电磁力的计算

麦克斯韦应力法是用等效的面积力代替体积力来计算交界面上的电磁应力，利用该方法，可求出U型电机定子表面受到的电磁力。设n、t为交界面上单位面积ds的单位法向量与单位切向量，则定子侧受到的电磁力的法向和切向分量为[15-16]：

由于电机铁芯的磁导率远远大于空气的磁导率，根据麦克斯韦张量理论，可将公式化简为：

2 电机转子偏心故障分析

2.1 转子偏心类型及解析模型

偏心是电机最常见的故障之一，偏心大体上可分为两种： 一种是静态偏心，指定、转子不同心，转子以自身几何轴心O'为旋转轴，即转子相对定子在某一方向上发生了偏移，且最小气隙的位置不发生变化如图4（a）所示; 另一种是动态偏心，指定、转子不同心，但转子以定子的几何轴心O为转轴，转子自身的几何轴心不断的变化，导致最小气隙磁密的位置随着时间的变化而变化，如图4（b）所示[17]。还有一些复杂的偏心都是由以上两种类型的组合，例如混合偏心。

2.2 转子偏心对磁场的影响

现利用软件分别得到理想状态下的模型以及偏心距为0.3mm时的静态偏心模型，由于在稳态场中静态偏心可以看做为动态偏心在某一时刻下的状态，所以利用有限元法只需分别得到无偏心和静态偏心这两种情况下的气隙磁密分布图，如图5、图6所示。

由图5、图6可知，当发生偏心时，会导致磁感应强度幅值增加，为更清晰的显示出偏心对气隙磁密的影响，利用气隙磁密处的云图进行观察，如图7所示。

由图7可知，当转子发生偏心时，电机内的气隙长度发生变化，气隙磁场整体向气隙较小的方向偏移，而且气隙磁密在偏心朝向处比偏心反向处的高，偏心朝向处的气隙磁密比不偏心时的气隙磁密增加0.02T，同样，偏心反向处气隙磁密比不偏心时幅值有所降低，磁密变化相对平缓。

为具体分析转子偏心距离对气隙磁密幅值的影响，表1给出了偏心距离对径向气隙磁密的影响。

从表1中可以看出，当电机转子发生静态偏心时，气隙磁密幅值随着偏心距离的增加而增加，并且该气隙磁密对应的空间角逐渐变小，即磁场向偏心方向偏移。

2.3 转子偏心对电磁转矩的影响

由于转子偏心改变了U型电机气隙内的磁场分布，从而对电磁转矩产生了影响。图8中给出了该电机空载时，其分别在无偏心、静偏心、动偏心状态下的电磁转矩。

由图 8可知，在偏心情况下，由于电机受到内部不对称气隙磁场的影响，使得电机在运行过程中，转子的电磁转矩出现了明显的变化，从而加重了电机振动和噪声。

为进一步分析出偏心对转矩的影响，以静态偏心为例进行分析。表2给出了电机在空载状态下发生静态偏心时转子偏移距离对转矩的影响。

由表2可知，该电机在空载状态下，随着转子偏心程度的增加，电机电磁转矩的平均值有所增大。转子偏心距为0.3mm时，与转子不偏心相比，电磁转矩的平均值增加了2.86%，但电磁转矩的波动振幅随转子偏心程度的增加而略有减小。由此可见，转子静偏心对电机电磁转矩有一定的影响。

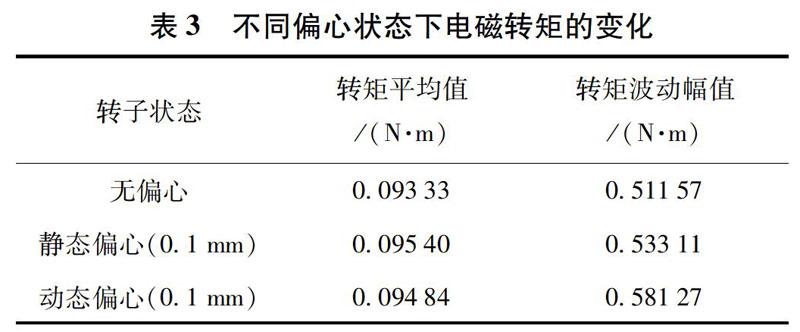
在静态偏心对电机转矩影响的基础上，表3给出了U型电机在空载状态下，不同偏心形式对电磁转矩的影响。

由表3可知，在U型单相自起动永磁同步电机中，静态偏心时电机转矩的平均值最大，且转矩的波动振幅相对较小，尽管变化不是很明显，但在降低转矩波动方面具有一定积极作用。动态偏心下电磁转矩的平均值略有增加，而转矩波动振幅有较大的增加，所以动态偏心将会增加电机转矩的波动，使电机的振动和噪声进一步恶化。

2.4 电磁力的分析

转子偏心引起磁场的改变，不仅直接影响了电磁转矩，同时也引起了电磁力的变化。发生偏心故障时，转子铁心受到不平衡磁拉力，在转子静态偏心状态下，转子所受到的不平衡磁拉力方向指向气隙小的一侧，致使转子的偏心程度加剧，对轴承造成损害。

研究发现，电机在运行时气隙磁密中含有丰富的谐波分量，会引起电机的振动和噪声，同时电机径向电磁激振力是造成电机振动和噪声的根本所在[6]。所以本节采用有限元计算，得到电磁力在空间、时间上的变化情况，以及电磁力的时、空频谱，研究在不同偏心状态下电磁激振力的变化情况。

图9和图10为U型单相永磁同步电机在不同的偏心状态下定子侧径向电磁力和切向电磁力随空间角度变化的情况。

從图9和图10中可以看出，电磁力波曲线波动较大，这是由于该电机采用不均匀气隙，且存在较大的定子齿槽，使得定子内径侧磁密出现较大的波动和局部突变;静态偏心产生的径、切向电磁力幅值大于无偏心情况下的电磁力，且动偏心状态下的电磁力波动最大。电机在正常运行时，其电磁力呈对称分布，但在偏心故障中气隙不再呈对称分布甚至是随时间变化的，这导致电机在偏心下产生更多谐波，所以加重了电机的振动和噪声。

为了进一步的讨论偏心故障对电磁力的影响，通过matlab将上述得到的径、切向电磁力进行傅里叶分解，分别得到图11和图12。

由图11和图12可知，在低阶次谐波中静态偏心的径、切向电磁力谐波幅值最大，这是由于静态偏心时，气隙偏向某一位置，使磁导和磁密具有倾向性，导致力的幅值增大;从图中还可以看出在静态偏心和动态偏心状态下径向电磁力波的1、3、5、7等奇次谐波幅值大于无偏心状态下的奇次谐波幅值。

同样，采用麦克斯韦应力张量法来计算定子内径侧气隙中某一点处的径、切向电磁力随时间的变化情况。图13和图14分别为转子在无偏心状态、静偏心和动偏心状态下的径、切向电磁力随时间的变化图。

从图13和图14中可以看出静态偏心时，这一点受到的电磁力的变化幅值是平稳的，而静态偏心和动态偏心时，电磁力的幅值变化不再是平稳的。

图15和图16是对上述得到的电磁力随时间变化的数据进行频谱分析，得到不同频率下的径、切向电磁力幅值。

从图15、图16中可知：在偏心状态下，电磁力并未产生新的频率，且动态偏心时会在50Hz和150Hz等低频率情况下产生很大的电磁力，而在高频率中静态偏心产生的电磁力更大。

3 结 论

本文运用有限元法和麦克斯韦应力法，针对U型单相自起动永磁同步电机的偏心故障进行仿真计算，得到转子偏心对该电机内的磁场、电磁转矩以及电磁力等的影响。并得出以下结论：

1）通过对该电机进行定量的分析计算，验证了转子偏心会导致电机内磁场分布不对称，出现局部气隙磁密过大的情况，并且气隙磁密的幅值随着偏心距离的增加而增加。

2）通过对该电机在三种偏心情况下的对比可以发现，转子静态偏心对电磁转矩及其波动影响较小，但在降低转矩波动方面具有一定积极作用。而在动态偏心时，会导致转矩的波动振幅有明显的增加，对电机的性能有很大影响。

3）转子偏心导致电磁力中1、3、5、7等奇次谐波分量增加，在偏心状态下，电磁力并未产生新的谐波分量，但动态偏心会使电磁力低频谐波分量大幅度增加，而静态偏心使高频率状态下的电磁力增加。

参 考 文 献：

[1] 付敏 于长胜 白宏哲等. 阶梯气隙结构对U型单相永磁电机自起动性能的影响[J]. 电机与控制学报 2010，14（16）：39-44.

[2] 付敏，邹继斌，李文娟等. U型单相自起动永磁同步电机参数计算与起动特性分析[J].微电机，2006，39（2）：22-25.

[3] 王凤翔，王晓鹏，高雅. U 型铁芯单相永磁同步电动机起动特性[J]. 沈阳工业大学学报 2009，31（1）：1-6.

[4] 付敏 邹继斌 戈宝军等. 新型单相永磁同步电机中导电套筒的作用及其对磁性能影响的研究[J]. 中国电机工程学报 2006，26（15）：150-155.

[5] 付敏，陈洋. U型单相永磁同步电机振动及噪声的有限元分析[J].哈尔滨理工大学学报，2015，20（3）：86-90.

[6] 毛可意. 大型汽轮发电机转子偏心故障动态分析[D]. 哈尔滨：哈尔滨理工大学 2015.

[7] 仇志坚，李琛，周晓燕，等. 表贴式永磁电机转子偏心空载气隙磁场解析[J]. 电工技术学报，2013，28（03）：114-121.

[8] 朱海峰，祝长生. 转子静偏心时异步电机径向力特性分析[J]. 机电工程，2013，30（08）：981-986.

[9] 孔汉，刘景林. 永磁伺服电机转子偏心对电机性能的影响研 究[J]. 电机与控制学报 2016，20（1）：52-59.

[10]狄冲，鲍晓华，王汉丰，等. 感应电机混合偏心情况下径向电磁激振力的研究[J]. 电工技术学报，2014，29（01）：138-144.

[11]李明，王巍. 转子静态偏心对电动汽车永磁同步电机转矩波动的影响[J]. 微电机，2016，49（04）：32-34+71.

[12]谢颖，冯春爽，杨忠学等. 笼型感应电动机断条故障前后转子电磁力计算及结构静力学分析[J]. 电工技术学报，2015，30（15）：164-171.

[13]王荀，邱阿瑞. 笼型异步电动机径向电磁力波的有限元计算[J]. 电工技术学报，2012，27（07）：109-117.

[14]汤蕴璆. 电机内的电磁场[M]. 2 版. 北京：机械工业出版社，1998：348-351.

[15]梁艳萍，刘金鹏，陈晶. 大型感应电动机单相短路故障动态力计算[J]. 中国电机工程学报，2012，32（09）：109-115+17.

[16]李志强，罗应立，蒙亮. 基于有限元的虚位移原理在汽轮发电机局部电磁力计算中的应用[J]. 中国电机工程学报，2007，27（15）：47-52.

[17]鲍晓华 吕强. 感应电机气隙偏心故障研究综述及展望[J].中国电机工程学报，2013，33（6）：93-100.

[18]SAMAGA R VITTAL K P. Air Gap Mixed Eccentricity Severity Detection in an Induction Motor[C]. IEEE Inter. Conf. on Recent Advances in Intelligent Computational Systems 2011： 115-119.

[19]王玎 祝长生 符嘉靖. 基于有限元的异步电机电磁振动分析[J].振动与冲击 2012，31（2）：140-144.

[20]SUBHASIS N RAJ M B HAMID A T. Mixed Eccentricity in Three Phase Induction Machines： Analysis Simulation and Experiments[C]//IEEE Inter. Conf. on Industry Application Conference 2002：1525-1532.

[21]刘金鹏. 高效高压感应电动机铁耗及电磁力分析计算[D].哈尔滨：哈尔滨理工大学，2011.

[22]RAHIDEH A KORAKIANITIS T. Analytical Open-circuit Magnetic Field Distribution of Slotless Brushless Permanent-magnet Machines with Rotor Eccentricity [J]. IEEE Transactions on Magnetics 2011 47（12）： 4791-4808.

（編辑：关 毅）