不同规模地形模型对某山区桥梁设计风特性确定的影响

2018-02-13刘黎阳张志田汪志雄

实验流体力学 2018年6期

刘黎阳, 张志田, 汪志雄, 汪磊

(1. 云南省交通投资建设集团有限公司, 昆明 650228; 2. 海南大学土木与建筑工程学院, 海口 570228; 3. 湖南大学土木工程学院, 长沙 410082; 4. 云南省交通规划设计研究院有限公司, 昆明 650041)

0 引言

中国中西部高速公路网的建设过程中，不可避免地会出现许多跨河、跨深切峡谷的大跨度桥梁。大跨度桥梁是柔性结构，对风效应敏感，因此抗风设计是保证这些大跨度桥梁安全的必不可少的环节。中国《公路桥梁抗风设计规范》(JTG/T D60-01-2004)[1]将桥梁所处的风环境分成4类。根据这4类场地，结合该地区的基本风速可得到桥面高度处的设计风速。《公路桥梁抗风设计规范》隐含了一个基本假定，即将地表特征如平坦的海面、起伏的山丘、林立的高楼等对大气边界层的影响等效成一种宏观的表面粗糙度，从而影响边界层内的平均风速分布梯度。这种处理方式在大范围内是有统计意义的，但不能处理局部风特性的问题。中国西部山区桥梁，或跨越非典型的山口，或跨越深切峡谷，所处地形千变万化，具有明显的局部风特性，因此桥址的设计风特性(如平均风速、湍流度、风迎角特性等)无法从《公路桥梁抗风设计规范》中得到合理取值。当前，山区大跨度桥梁合理设计风特性的取值仍然是一个没有解决的问题。

针对特殊地形下的风特性，国内外研究者进行了一系列的研究。Miller与Davenport等[2]率先对山区复杂地形中的风速加速效应特性做了一系列研究；Sierputowski等[3]、Bullard等[4]用简化的梯形状山体制作了山谷模型并进行了风洞试验。该研究对于位于地表主平面之上的山谷风特性具有一定的参考意义，但对位于地表主平面之下的深切峡谷无参考价值。Takahashi等[5]研究了一孤立山体周围的风特性，结果表明山顶的风速加速效应受山体粗糙度(植被覆盖程度)的影响。Kondo[6]、Lubitz[7]等则研究了沿一个孤立的简单山坡上的风速分布特性。Bowen[8]利用简单的山包线性排列成连续起伏的地形并进行了试验研究，结果表明山体对风场的影响遍及任意方位，其影响范围至少是2倍的山体直径。Yamaguchi等[9]针对实际复杂地形制作模型进行了风洞试验研究，结果表明在复杂地形区域很难应用规范中的指数规律来描述平均风特性，也不能依照公式从低海拔处的湍流特性推出高海拔处的湍流特性。陈政清等[10]采用地形模型试验方法对矮寨大桥的设计风特性进行了研究，结果表明桥址的风迎角、湍流度、风谱等与规范取值存在明显差异。白桦等[11]对三水河大桥进行了地形模型试验研究，结果表明该桥址没有明显的峡谷效应，但湍流度大。张玥等[12]对禹门口黄河大桥进行了地形模型试验研究，结果表明桥面风特性与规范结果差异明显。Li 等[13]对处于深切峡谷地带的龙江大桥进行了地形模型试验研究，结果表明平均风剖面从谷底往上变化复杂，必须分阶段进行描述。

在山区桥梁的抗风研究中，设计风特性常通过地形模型风洞试验来确定。地形模型风洞试验本身无法定量地确定设计风速值的大小，但通常可以确定平均风速分布的定性规律、风迎角以及基本的湍流特性。然而，地形模型所覆盖的范围总是有限的，不同范围大小的地形模型对桥址的风特性试验结果必然存在影响，但影响有多大，地形模型范围应当取多大是一个尚待研究的问题。

1 地形模型试验

1.1 模型制作

图1为某悬索桥的立面设计方案，该桥主跨约920m，跨越典型的深切峡谷。图2为该桥桥址Google地形，图中实线表示加劲梁位置。该桥址的峡谷两岸为起伏不大的丘陵地貌。在垂直桥轴线的上游，峡谷走向接近正北方向；在下游，峡谷走向为东南方向。

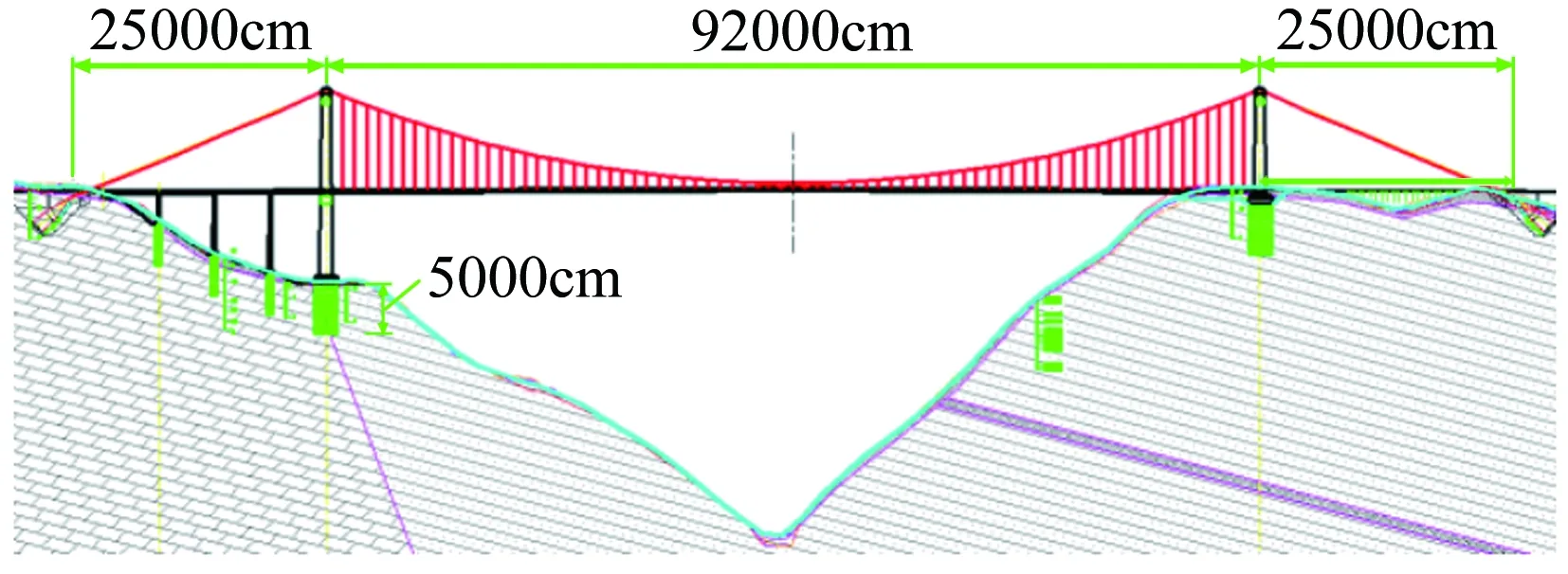
图1 某悬索桥立面设计方案

由图可知，该桥所在环境的局部风特性非常明显，根据中国《公路桥梁抗风设计规范》无法给出合理的设计风特性(如风迎角、湍流度和平均风速等),因此，地形模型试验结果可提供有价值的参考。为研究不同规模地形模型对试验结果的影响，制作4组不同规模的地形模型进行风洞试验，主要测试加劲梁高度处的风特性。图2分别给出4组不同规模的地形模型,表1给出了4组模型在东西(EW)、南北(SN)方向所覆盖的实际地形跨度，其中最大的A模型覆盖地形范围水平投影面积为25km2，最小的D地形模型仅覆盖1km2。地形模型缩尺比为1∶1000，A、B、C、D 4组模型在风洞中的阻塞比分别为8.8%、8.8%、3.9%和1.2%。图3给出了4组地形模型在风洞中的照片。

图2 4组不同地形模型的规模

图3 风洞中的4组地形模型

表1 4组模型的地形跨度Table 1 Terrain spans in the 4 models

以桥轴线所在位置处的峡谷宽度与高度的平均值为特征尺度，对地形模型无量纲尺度η定义如下：

(1)

根据本文定义的桥位处峡谷的特征尺度与式(1)可得到4组地形模型的无量纲半宽度、从桥中心到东边以及西边的无量纲距离，如图4所示。

图4 地形模型的无量纲尺度

1.2 风洞试验

风洞试验中，按B类场地采用尖劈+粗糙元的方法模拟无穷远处的来流特性，如图5所示。图6给出来流模拟得到的平均风速剖面以及3个方向的湍流度剖面，其中，Iuu为顺风向湍流度,Ivv为横风向湍流度，Iww为竖向脉动风湍流度。采用2个眼镜蛇探头进行风特性测试，如图7所示。眼镜蛇探头具有圆锥体的设计特点，可测试与探头主轴夹角在±45°范围内的来流风速，该范围内风速测试的典型误差为0.5m/s。探头1固定放置于地形模型前风速稳定的区域，并位于风速无明显变化的高度范围；探头2安装于风洞顶壁的电控移测架上，可前后、上下、左右移动，用于测试所关心位置的风特性。

图5 来流风场模拟

试验结果表明，来流风速一定的情况下，风向与河谷走向一致时,加劲梁高度处的风速接近最大。因此，东南(SE)方向为最不利风向工况。此外，SE风向时，由于气流顺着与风洞底板齐平的谷底进入，风特性受地形截断的影响最小。鉴于这2个因素，以下固定SE风向来探讨不同规模地形模型对试验结果的影响。对于该风向，桥位到地形东端的无量纲距离将为影响风场特性的控制因素。由图4可知，4组模型在该方向的无量纲跨度分别为5.20、3.70、2.20、0.75。

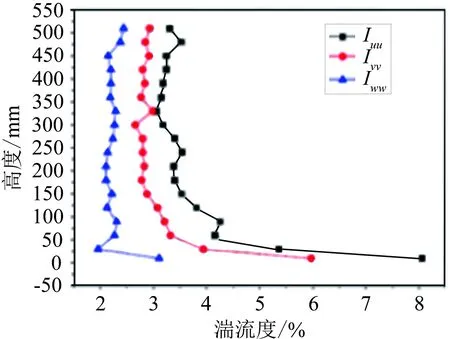
图6 来流平均风及湍流度剖面

Fig.6Themeanwindandturbulenceintensityprofilesoftheincomingflow

图7 眼镜蛇探头布置

2 平均风特性

2.1 平均风速特性

用眼镜蛇探头2所测得的山谷中的平均风速除以来流风速(探头1所测风速,其位置见图7)可得归一化风速。图8给出了左桥塔位置处归一化的平均风速剖面。从图中可知，A、B、C 3组不同范围的地形模型所得到的结果已经没有明显的规模效应，表明3组模型的地形规模均已经足够大而形成稳定的平均风剖面，其中A模型的结果位于B、C 2组模型结果之间。然而，最小的D模型所得到的结果与其他3组结果具有实质性的区别，具体体现在两方面：(1) 风剖面更陡峭，即风速沿高度上升得更快；(2) 风速数值明显低于A、B、C 3组结果，峡谷风速增大效应在D模型上基本消失。显然，D模型的地形模型还不足以形成能够反应实际情况的平均风场。

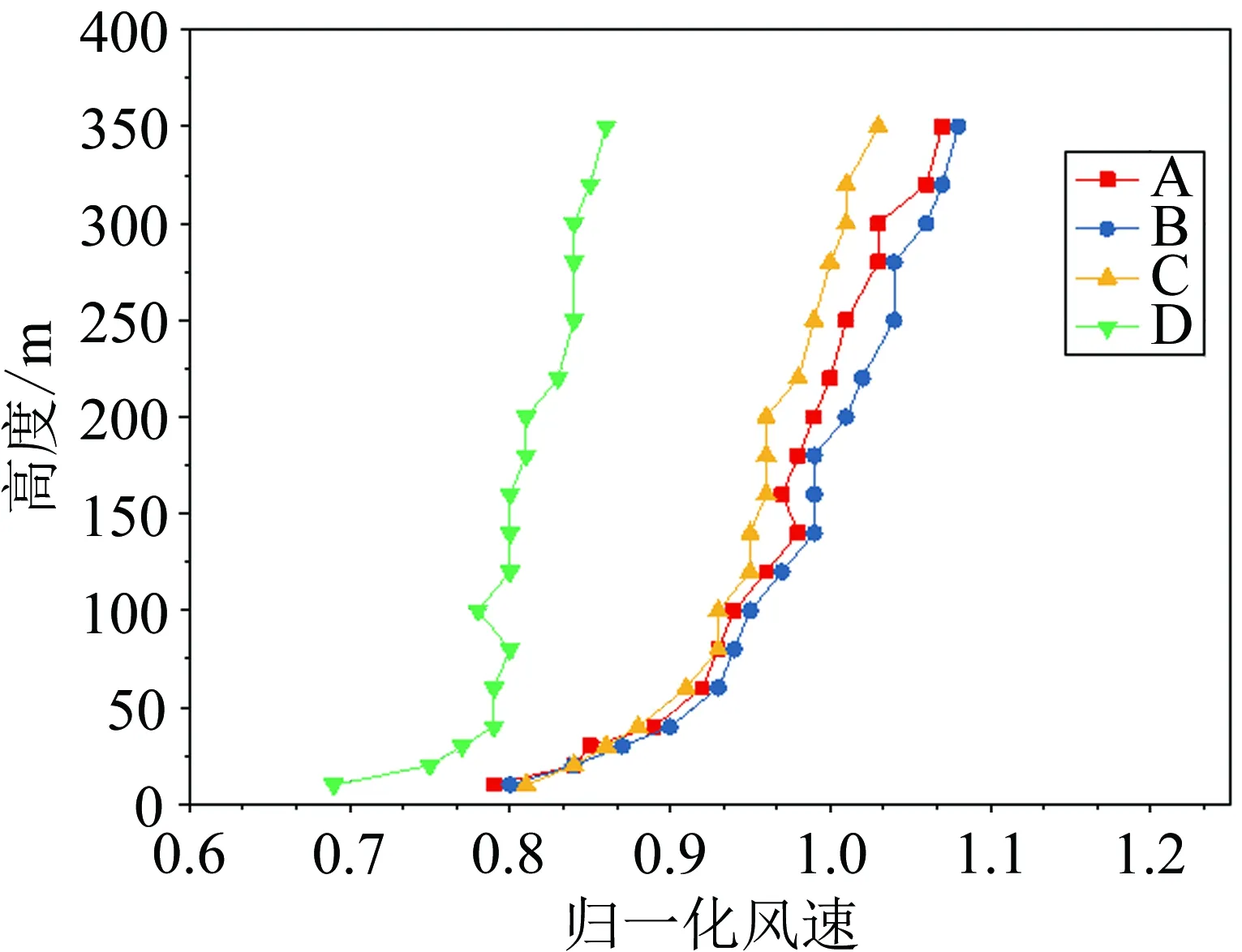
图8 左桥塔处归一化风速剖面

图9给出加劲梁几个主要控制点以及2个桥塔塔顶的归一化平均风速。从图中同样可以看出4组不同规模地形模型之间的差异。与垂直方向的风剖面类似，A、B、C 3组模型的测试结果比较接近，尤其是A、B 2组模型的结果已经非常接近。但三者与D模型之间的差距明显，主要体现在两方面：(1) 风速差距明显，最大达到30%左右；(2) 相比之下，D模型加劲梁3个控制点与两塔顶的风速差异不明显。

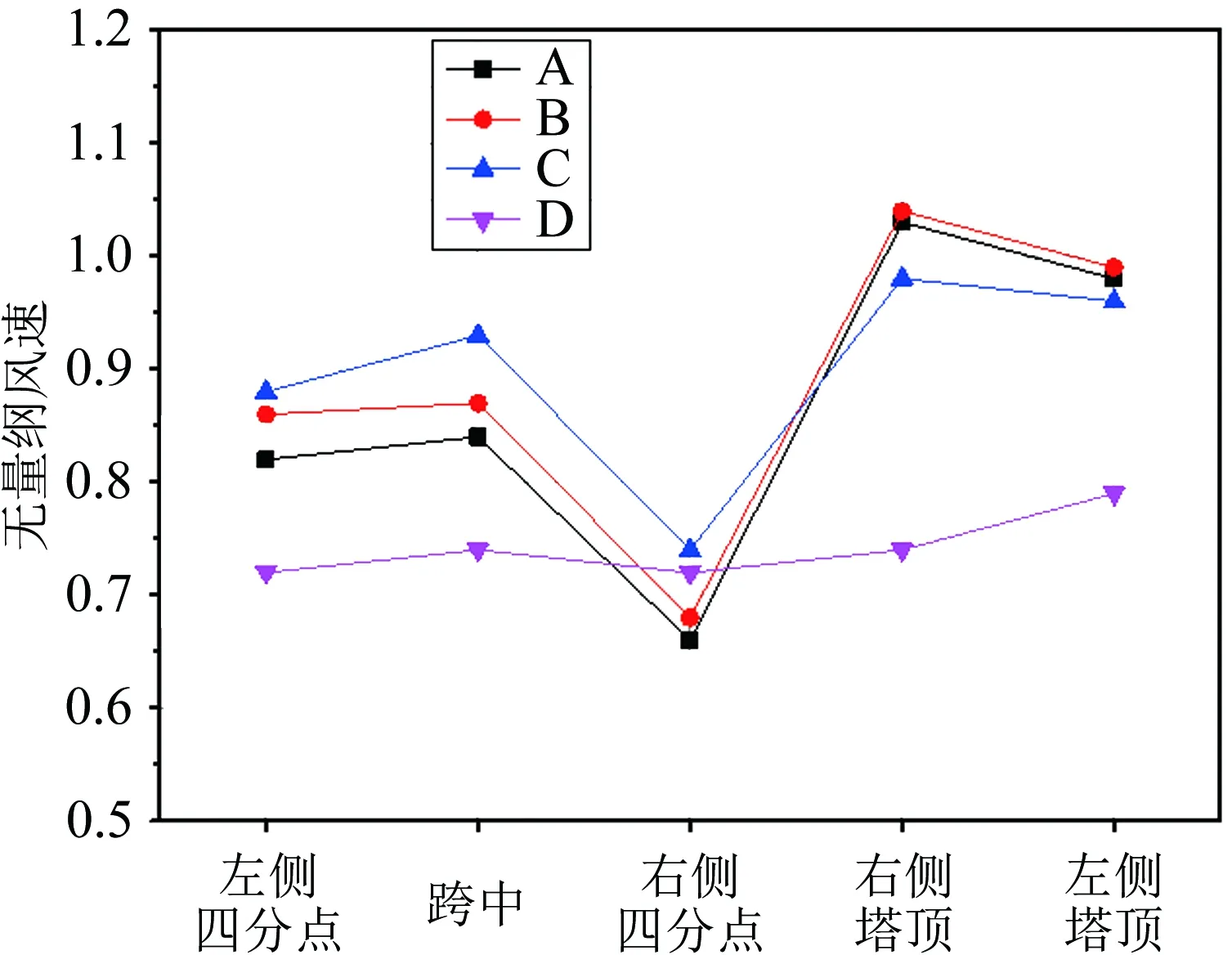
图9 主要控制点的归一化风速

2.2 平均风迎角特性

图10给出各控制点所测得的平均风迎角。由图可知：(1) A、B 2组规模的地形模型所得到的结果已经基本一致，C规模模型所得到结果在右侧塔顶与A、B 2组模型有较大差异，其他点基本一致；(2) D模型测试结果与前3组模型差异明显，集中体现在回劲梁跨中、右侧四分点以及右桥塔顶；(3)与《公路桥梁抗风设计规范》建议的±3°风迎角相比，本文试验所得风迎角远超出规范建议的范围。从较稳定的A、B 2组模型的试验结果来看，加劲梁位置处风迎角沿水平向变化剧烈，最大约为+2°，最小为-10°。

图10 主要控制点的平均风迎角

3 湍流特性

3.1 湍流度特性

图11给出了左桥塔位置处4组模型所测得的湍流度剖面。从图中可知4组模型所得到的湍流度剖面各不相同，没有因为地形规模的增大而收敛。这说明，就湍流度剖面而言，目前所使用的地形规模还不够大。另一方面，D模型的湍流度剖面在高度50～350m之间基本没变化，保持在9%左右，这一特征与另外3个剖面明显不同。

图11 左桥塔位置处湍流度剖面Iuu

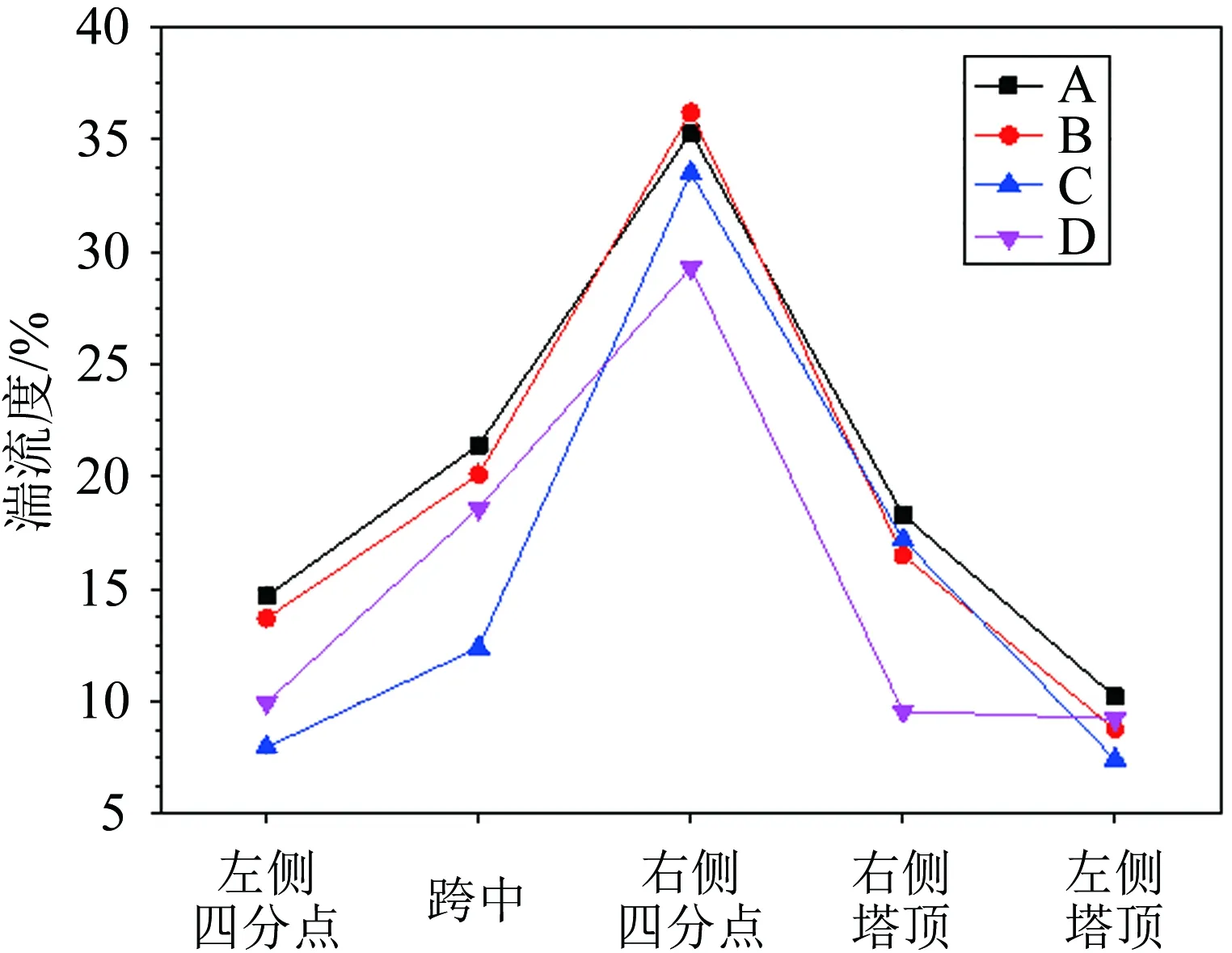
图12给出桥面高度处各控制点的湍流度。从图中可知，对于顺风向湍流度Iuu，A、B 2组模型已经基本上取得较一致的结果，表明其规模效应已接近“收敛”，而C、D 2组模型则因规模明显不足而表现出与A、B 2组模型结果有较大差距。竖向脉动风湍流度Iww与顺风向类似。在两塔塔顶，A、B、C模型基本取得了一致的结果，表明3组模型的规模在塔顶均满足“收敛”要求。但在加劲梁位置C模型与A、B 2组模型存在明显的差距。相比之下，D模型的结果相差较大，表明其地形规模不能满足要求。

3.2 湍流功率谱

图13给出了左桥塔以及加劲梁跨中的脉动风功率谱。从图中可知，左桥塔100m高处，4组地形模型得到的顺风向脉动风功率谱没有十分明显的差异。相比而言，竖向脉动风功率谱相差较明显。与Kaimal谱相比，顺风向功率谱在低频处相差较大，而竖向功率谱则有相同的趋势。对于加劲梁高度处的脉动风功率谱，A、B 2组模型已经十分接近，而D模型所得到的功率谱在高频处与前三者有明显的差距。