“ 高度”成就“ 深度”

季云

【教学片段1】感受平均数的概念

师：喜欢“打地鼠”的游戏吗？

出示小林1分钟打地鼠的成绩：玩了3次，平均每次打4个。

师：是不是一定每次都打4个呢？你觉得有可能每次分别打了几个呢？

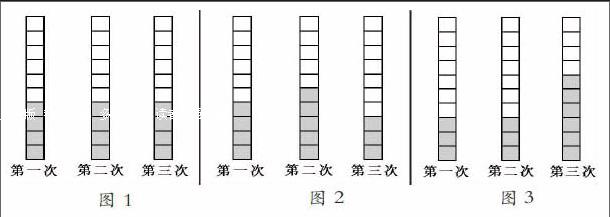
学生自主在条形方格图中画一画。

展示交流学生作品：

师（指图2、图3）：怎样才能证明平均每次打4个呢？

生1（指图2）：把第二次拿1个给第三次，每次打的都是4个了。

师：可以移多补少。

生2（指图3）：也可以算一算，用3+3+6=12（个），求出3次一共打了12个，再除以3次，算出平均每次4个。

师：还可以计算。以前，当我们看到“平均每次打4个”时，最先想到的是什么？

生：每次都是4个。

师：现在看来，是不是每次一定都是4个呢？

生：有可能每次都是4个，也有可能每次的个数不一样。

师：我们把这个很有趣的数叫做平均数。（板书：平均数）

【赏析】对于平均数，学生有着一定的生活经验和应用基础。魏老师的教学紧密围绕“平均每次打4个，是不是一定每次都打4个呢”这一十分具体的问题，逆向性地展开。学生通过操作和思考体会平均数的含义，并在“怎样才能证明平均每次打4个”的过程中学会灵活地运用“移多补少”和“计算”的方法求简单的平均数。使学生感受到平均数实质上反映的是一组数据的“平均大小”，体现的是一组数据总体的“平均水平”。

【教学片段2】体会“整体水平”的含义

出示统计图4

小林3次打地鼠情况统计图

师：可以用5来表示三次的平均水平吗？3呢？

生：5比3和4都大，3比4和5都小，不行。

师：用几可以表示出3次的整体水平呢？

生：4可以表示3次的整体水平，4比3多1个，比5少1个，刚好。

出示统计图5。

师：可以用6来表示3次的平均水平吗？3呢？

生：不行，6比3大，3比6小，也不能刚好移多补少。

师：不能用6，也不能用3，那可以是4或5，为什么不是5，而是4呢？

生：6只比5多1，不能使每一次的成绩都达到5。

出示统计图6。

师：3、4、5的时候，5太多、3太少，用4正好；而3、3、6的时候，3太少、6太多，选4正好。看来，4可以代表这组数据的整体水平。

师：这里的4可以代表哪些数据的整体水平？

生：第一组代表3、4、5的整体水平，第二组代表3、3、6的整体水平。

【赏析】如何使学生体会到平均数是反映一组数据“整体水平”的数据？魏老师的教学结合直条图，直观形象，让学生在思考、操作中进一步认识到“用来代表一组数据整体水平的那个数，应该与该组数据中的每个数都有联系”，初步体会到平均数的含义和大小范围区间。

【教学片段3】理解平均数的实际意义

1. 运动数据。

课件出示：全国平均3475步，自己排名第84名，跑了4687步。

师：怎样知道自己的跑步成绩有没有拖后腿？

生：和全国平均步数3475比，老师的成绩要高出1000多，所以成绩要高于平均水平。

2. 大数据显示：“双十一”白领人均消费金额2101元。

师：是不是所有的人消费金额都是2101元呢？

生：也许有的白领消费超过了2101元，也许有的还不到2101元，也有可能刚好是2101元。

3. 第五次儿童体格发育调查结果：我国9岁儿童平均体重25千克，10岁儿童平均体重35千克；我国9岁儿童平均身高135厘米，10岁儿童平均身高141厘米。

师：读一读这些平均数，和自己的身高体重比一比。

生1：我的体重45千克，和全国10岁儿童的平均体重相比，我发现自己太胖了。

生2：我的身高是134厘米，和全国9岁儿童的平均身高相比，接近平均水平。

师：提供这样的数据再比一比，有用吗？

生：有用，可以知道自己的体重和平均水平相比是过重还是过轻，身高是偏高还是偏矮。

师：体重过重怎么办？过轻呢？

师：可以了解到相关的信息，从而知道自己该怎样做。

师：这里的数据是怎样得到的？

生：把全国的这个年纪的儿童的体重和身高加起来，再除以总人数，算出平均每人的体重和身高。

师：这个数据可靠吗？

生：可靠，是调查全国所有人而得到的，代表的是全国的平均水平。

【赏析】理解平均数的实际意义是统计教学的核心。学生理解了平均数的意义，才能用平均数去刻画、描述、表达、分析数据，应用于实际问题中。教学中，魏老师引导学生运用平均数的知识解释生活中的现象，分析和解决实际问题，以此使学生体会到“平均数”的实质和作用，加强学生对平均数实际意义的理解，进一步积累分析和处理数据的方法，发展统计观念。

【教学片段4】体会平均数的“虚拟”和“范围”

1.感受平均数的“虚拟”。

（1）课件出示：2015年南京市成年居民人均纸质图书的阅读量为5.34本。

师：平均5.34本，出现了小数，是不是每人读的书都不是整本书呢？

生：不是，读的总本数是整数，但是平均分给每个人就出现了不满1本的情况。

（2）继续出示：2015年南京市0～17岁未成年人的人均纸质图书阅读量为10.06本。

师：对比两个数据，你发现了什么？

生：未成年人读的书是成人的近2倍，成人读的书太少了。

2.体会平均数的“范围”。

师：四年级一班第一小组的男、女生进行套圈比赛，每人套15个。下面的统计图表示他们套中的个数。（图7）

师：男生套得准一些，还是女生套得准一些？你想怎样比？

生：不能拿一个数去比较，比整体水平，比套圈的平均个数。

师：男生平均每人套几个？平均数大概在哪个位置？

生：比9少，比5多。

师：女生套圈的平均个数我估计是7，你认为对不对？

生：如果是7的话，吴燕给刘晓娟3个，还有孙芸、沈明芳没补完。

师：你估计是几？平均个数有没有大小范围？

生：平均数一定在最多的和最少的之间。

师生明确：男生平均每人套中7个，“7”是6、9、7、6這4个数的平均数；女生平均每人套中6个，“6”是10、4、7、5、4这5个数的平均数。

师：男生套得准一些还是女生套得准一些？

【赏析】学生对平均数的理解，始终还停留在“一个具体的数”的层面上，如何使学生实现从“具体”到“虚拟”的抽象和过渡，真正感受到平均数只是一种“代表水平”呢？魏老师的教学借助对实际生活中的一些数据的分析和解释，帮助学生彻底跳出原来的“框”，使学生对平均数的认识上升到一个新的高度。最后，魏老师通过比较“男生套得准一些还是女生套得准一些”这个实际问题的解决，加深学生用平均数描述数据、分析问题的体验，丰富平均数应用的现实背景及它的实际作用，深化他们对平均数的认识。endprint