考虑横向惯性效应时饱和土中大直径桩的纵向振动研究
2018-02-10龚志超杨冬英
龚志超, 杨冬英
(苏州科技大学 土木工程学院,江苏 苏州 215011)
桩-土耦合振动问题的难点之一就是如何建立合理的土介质模型,纵观现有的研究成果,有将桩周土视为单相介质,不考虑液相(土中水)的影响,比如Keshavarz、Wang、吴文兵等[1-3];有将土视为固液两相介质的,即桩周土体为饱和土比如Zeng、Wang、李强、杨骁、刘林超等[4-10],对饱和土中单桩纵向振动特性进行了研究;也有将土视为非饱和土来研究桩-土耦合振动问题,比如张智卿、王星华等[11-12],对非饱和土中单桩的纵向振动进行了理论与试验研究,取得了丰硕的成果。其中,现代工程中,由于工程规模日趋变大,大直径桩运用范围极广,而大直径桩的振动特性与普通直径桩的动力特性有所区别,李强等基于Biot饱和土理论并将桩等效为Rayleigh-Love杆研究了饱和土中大直径嵌岩桩的纵向振动问题,指出了大直径桩不同于普通直径桩的振动特性。刘林超等基于饱和多孔介质理论,利用Novak薄层法[13]研究了饱和土中桩基的纵向振动问题,得出了桩顶导纳和桩顶复刚度的表达式,并将研究结果与三维模型的结果对比验证了结果的正确性。杨骁等基于饱和多孔介质理论,研究了考虑横向惯性效应时成层饱和土中单桩纵向振动特性,得出饱和土中桩顶复刚度的解析解。
在桩受纵向动力荷载作用时,不仅产生纵向变形,横向变形也会随之产生。在小应变情况下横向变形是否能够忽略不计跟桩的尺寸有关,已有研究结果[14]表明对于大直径桩来说不能忽略桩身的横向变形对桩基纵向振动的影响。为了既能合理反映饱和土中大直径桩振动问题,又能使此耦合问题方便解耦获取大直径桩-土耦合振动解,本文基于饱和多孔介质理论和Novak薄层法,考虑桩的横向惯性效应,建立饱和土中桩基的纵向振动模型,并分析水的体积分数、桩径等参数对桩顶动力响应的影响,以丰富饱和土中桩基的振动理论。
1 数学模型与基本假定
本文研究的是均质饱和土中桩基的纵向振动特性,桩-土耦合作用模型如图1所示。各向同性的均质饱和土中有一桩长为H、桩半径为r0的黏弹性摩擦桩,桩顶受到竖向振动力q(t) 的作用,桩周饱和土体对桩身单位长度上的摩擦力f(z)=2πr0τ。为简化计算,作出以下假定:①桩为等截面的粘弹性桩,弹性模量和材料阻尼分别为Ep和ηp;②桩底为黏弹性支承,桩底分布式(单位面积上)弹性系数和阻尼系数分别为kb、ηb;③桩周土体为固液两相饱和多孔介质,并且径向无限延伸;④桩与桩侧土完全接触,没有相对滑移和脱离,桩侧土体对桩的作用力通过桩侧土复刚度传递。
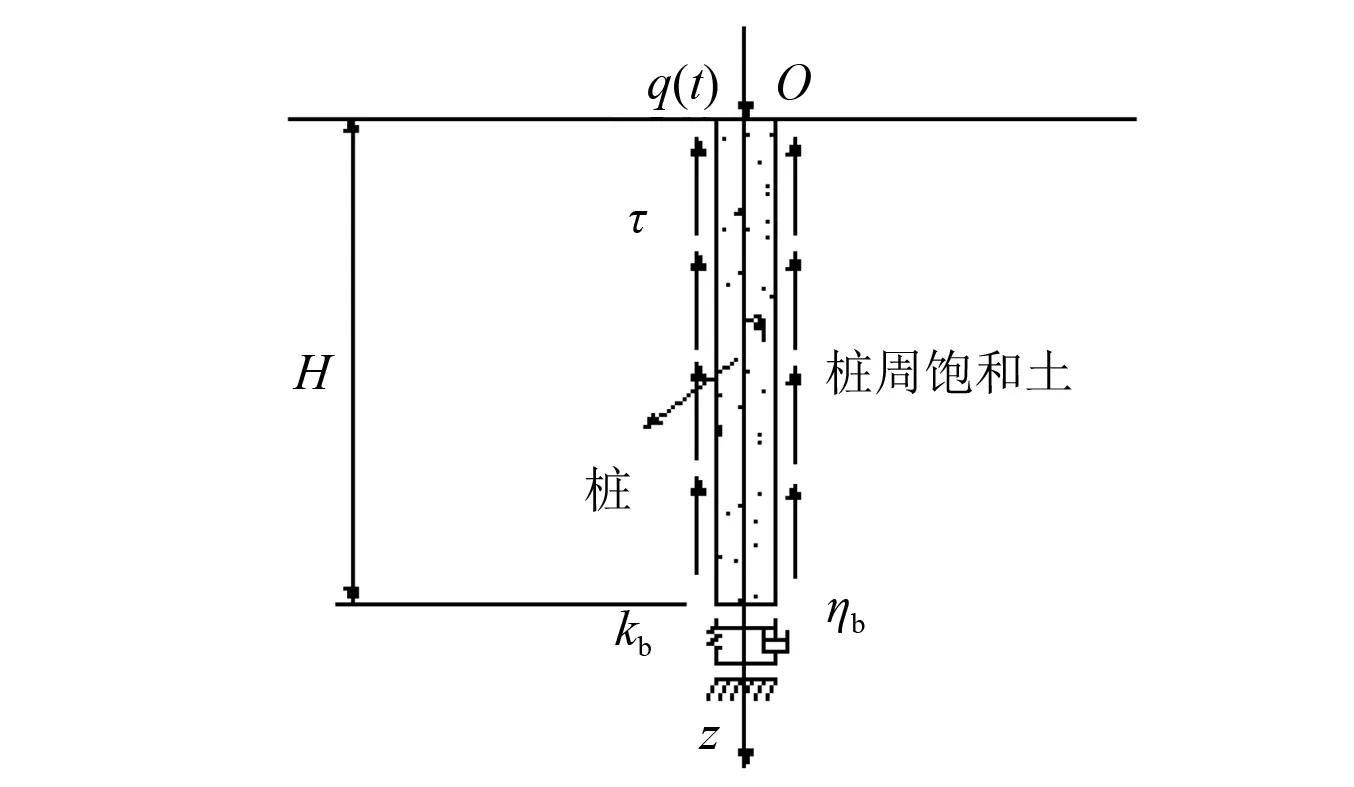
图1 桩-饱和土相互作用模型Fig.1 Model of saturated soil-pile interaction
2 饱和土体的动力响应
基于饱和多孔介质理论和Novak薄层法的假定可知饱和土体的动力控制方程[9]为
(1)
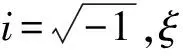
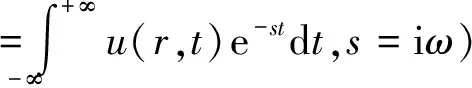
(2)
式中:
解方程式(2)得
(3)
式中:I0和K0分别为零阶的第一类和零阶的第二类虚宗量的Bessel函数,A和B分别为待定复系数。由于无穷远处土体位移为零,可得B=0,所以
(4)
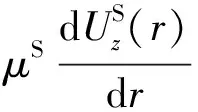
(5)
3 桩的纵向振动方程与求解
通过Hamilton变分原理[16]可知考虑横向惯性效应时桩的任一截面z处所受的截面力为
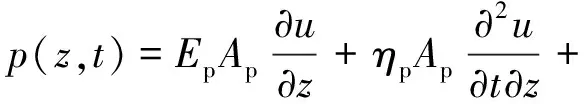
(6)
式中:Ep、Ap、ηp、υp、ρp分别为桩的弹性模量、截面面积、材料阻尼、泊松比、桩身密度,u=u(z,t)。在桩的任一截面z处取一微元段隔离体进行受力分析,可得考虑横向惯性效应时桩的纵向振动方程:
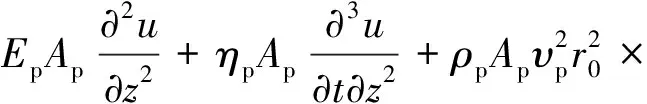
(7)
桩顶和桩底处的边界条件分别为
(8)
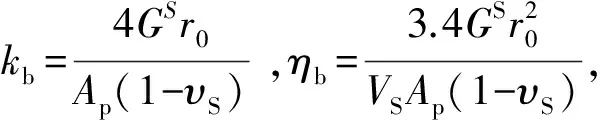
初始条件为
(9)
结合初始条件(9)对纵向振动方程(6)进行Laplace变换并进行整理可得
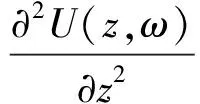
(10)

U(z,ω)=D1cos(λz)+D2sin(λz)
(11)
式中:D1和D2为待定系数,由边界条件决定。
由位移阻抗函数的定义(力除以位移)并结合桩底边界条件可得桩顶位移阻抗函数,即桩顶复刚度为
(12)

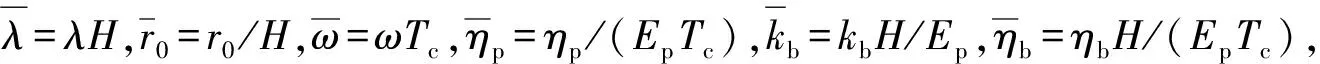
Zp0=Kr+iKi
其中Kr为动刚度,Ki为动阻尼。
由式(12)可得无量纲化桩顶位移阻抗函数为


(13)
桩顶速度频域响应函数为
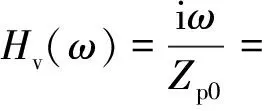
(14)
对Hv(ω)进行无量纲化可得
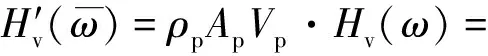
(15)
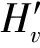
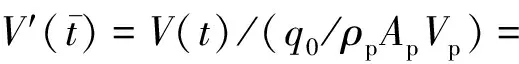
(16)
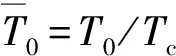
4 参数影响与分析
4.1 桩径不同时横向惯性效应对桩顶动力响应的影响
当令桩的泊松比为0时即可得到桩顶动力响应的一维解,图2~图5反映的是在其他参数不变的情况下(nL=0.33,nS=0.67),桩半径分别为r0=1.0 m和r0=0.4 m时桩的横向惯性效应对大直径桩顶动力响应的影响。
从图2(a)桩顶速度时域响应曲线可以看出,由于考虑横向惯性效应时波的传播过程中产生弥散作用,使桩底反射信号的波谷值明显减小,反射峰值的位置明显延迟,且反射波曲线出现剧烈震荡,这将会影响对桩底支承情况的判断;从图2(b)桩顶导纳曲线可以看出,在低频段横向惯性效应对桩顶导纳的影响几乎可以忽略,但随着无量纲角频率的增大,共振频率有所减小。这是由于桩的横向变形使波在桩中的传播是弥散的,较高的激振频率会引起较大的能量损失。同时也说明,对于饱和土中大直径桩基动力检测,应对反射信号在桩底附近振荡的原因加以区别。通过图2、图4的比较可以看出,当桩径明显减小时,横向惯性效应对桩顶速度时域响应和桩顶导纳的影响明显减小,几乎可以忽略。
图3、图5反映了大直径桩的横向惯性效应对桩顶复刚度的影响。从图3中可以看出在低频段,横向惯性效应对桩顶复刚度的影响可以忽略,但在高频段,是否考虑横向惯性效应将对大直径桩顶复刚度产生明显的影响:考虑横向惯性效应会使桩顶复刚度的峰值减小,并且频率越大,峰值差越大;通过图3与图5的比较可以看出,当桩径明显减小时,无论是低频段还是高频段,横向惯性效应对桩顶复刚度的影响均明显减小,甚至可以忽略。综合图2~图5的结论可以说明对于大直径桩而言,有必要考虑横向惯性效应对桩顶动力响应的影响,而忽略横向惯性效应的一维解只适用于细长桩。
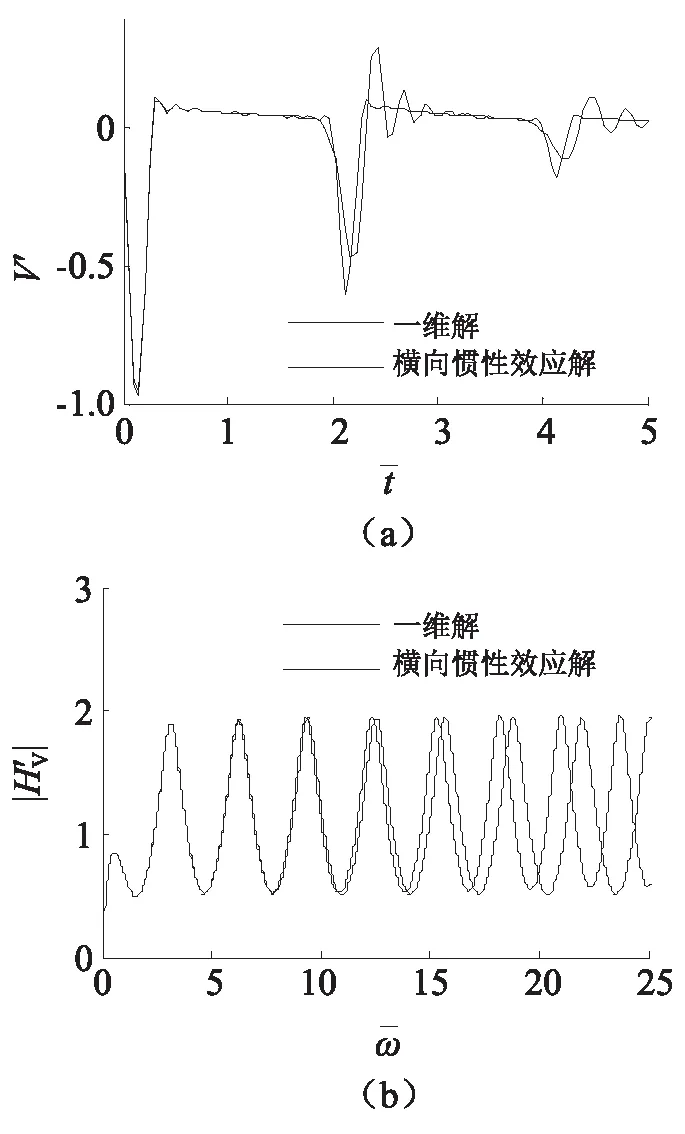
图2 桩的横向惯性效应对桩顶速度响应的影响(r0=1.0 m)Fig.2 Influence of transversal inertia effect on velocity response at top of pile(r0=1.0 m)
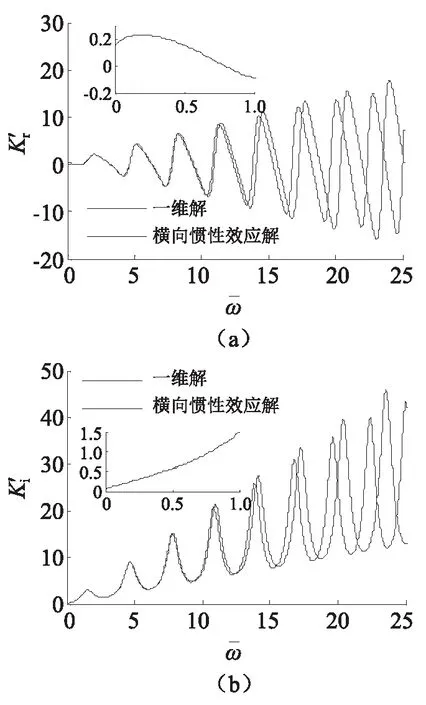
图3 桩的横向惯性效应对桩顶复刚度的影响(r0=1.0 m)Fig.3 Influence of transversal inertia effect on complex stiffness at top of pile(r0=1.0 m)
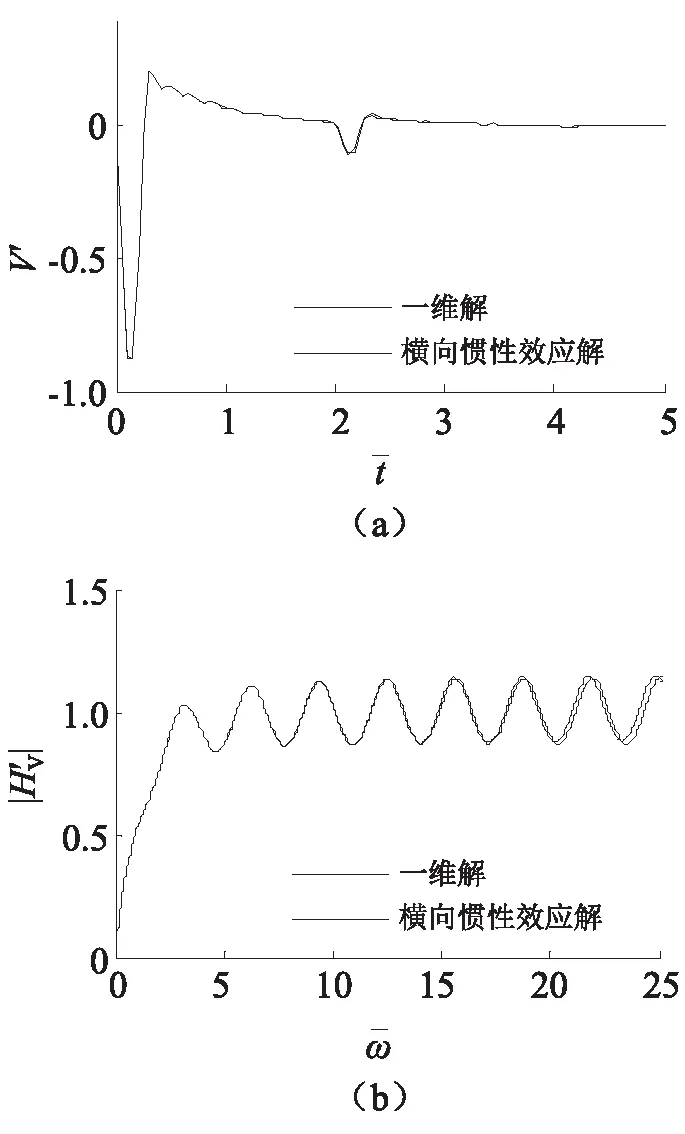
图4 桩的横向惯性效应对桩顶速度响应的影响(r0=0.4 m)Fig.4 Influence of transversal inertia effect on velocity response at top of pile(r0=0.4 m)
4.2 桩径对桩顶动力响应的影响
图6、图7反映的是在其他条件不变的情况下(nL=0.33,nS=0.67),桩径对桩顶动力响应的影响。
从图6(a)中的桩顶速度时域响应曲线可得,随着桩径的增大,桩底反射信号幅值明显增大,同时速度时域响应曲线的振荡也明显加剧。从图6(b)中可得,桩径越大,导纳曲线的幅值越大,共振频率越小。而在一维解中,桩径的增大并不会引起速度时域响应曲线的振荡,也不会使共振频率减小[17],这是由于受桩的横向惯性效应的影响,且桩径越大,影响越大。
图7反映的是在其他条件不变的情况下,在低频范围内桩径的变化对桩顶复刚度的影响。从桩顶动刚度曲线可得,在低频范围内,桩半径越大,桩顶动刚度越小;随着激振频率的增大,桩顶动刚度先增大后减小,且桩半径越大衰减的越快。从桩顶动阻尼曲线可得,当桩半径不变时,激振频率越大,桩顶动阻尼越大;对于同一激振频率,桩半径越大,桩顶动阻尼越小。
4.3 水的体积分数对桩顶动力响应的影响
图8反映的是在其他参数都不变的情况下(其中r0=0.8 m),水的体积分数对桩顶速度响应的影响(水的体积分数是指饱和土中水的体积与土体总体积的比值)。从图中可以看出,饱和土中水的体积分数越大,桩底反射信号幅值越大,桩顶导纳的幅值也越大,这是由于水的体积分数提高导致土体剪切模量降低的原因。

图5 桩的横向惯性效应对桩顶复刚度的影响(r0=0.4 m)Fig.5 Influence of transversal inertia effect on complex stiffness at top of pile(r0=0.4 m)

图6 桩的半径对桩顶速度响应的影响Fig.6 Influence of radius on velocity response at top of pile
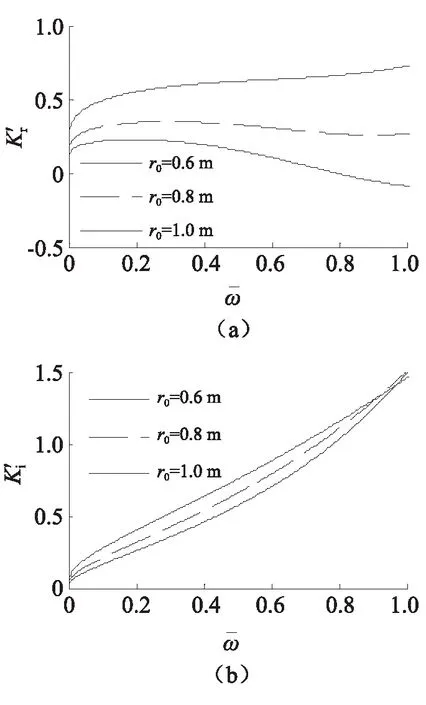
图7 桩的半径对桩顶复刚度的影响Fig.7 Influence of radius on complex stiffness at top of pile
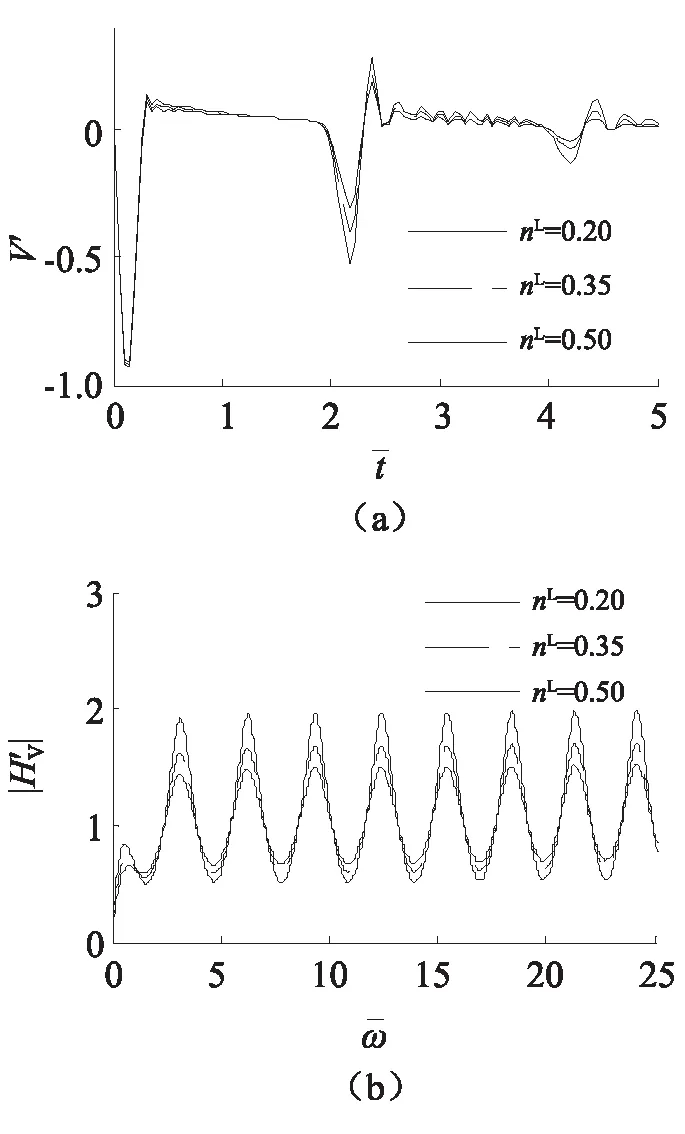
图8 水的体积分数对桩顶速度响应的影响Fig.8 Influence of water volume fraction on velocity response at top of pile
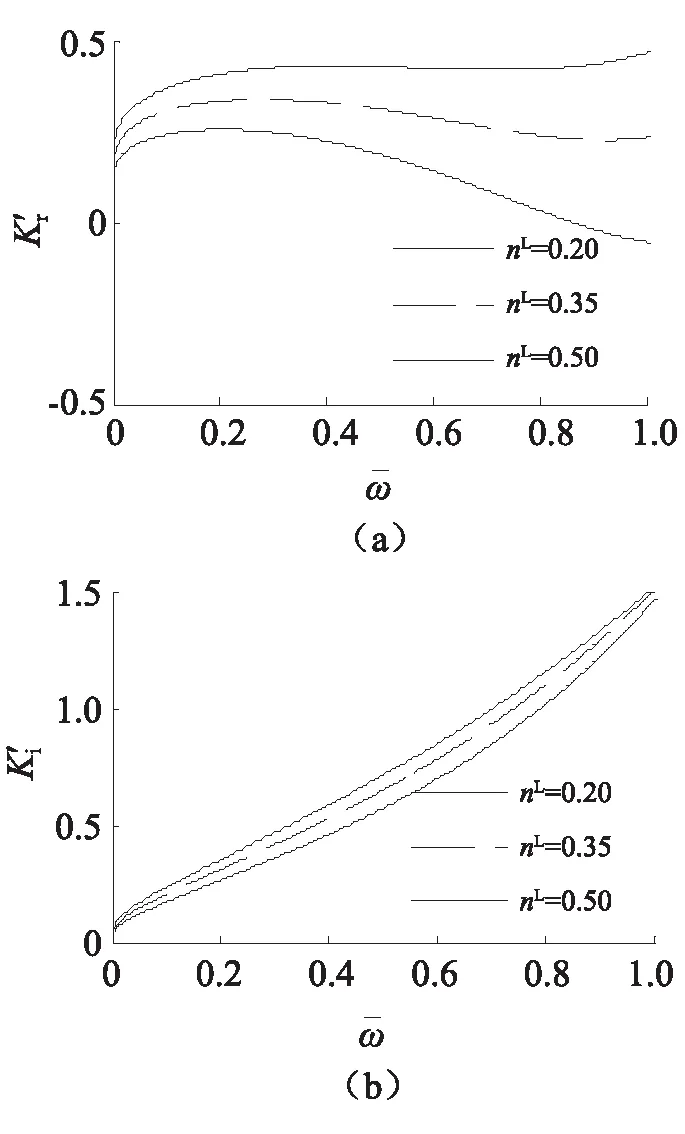
图9 水的体积分数对桩顶复刚度的影响Fig.9 Influence of water volume fraction on complex stiffness at top of pile
图9反映的是在其他参数不变时,在低频阶段,饱和土中水的体积分数对桩顶复刚度的影响。在激振频率不变时,随着水的体积分数的增加,桩顶动刚度明显减小,桩底动阻尼亦减小;在水体积分数不变时,随着激振频率的增加,桩顶动刚度先增加后降低,且水的体积分数越大衰减的越快,而桩底动阻尼随着激振频率的增加而增加。
5 结 论
本文分析了均质饱和土中考虑横向惯性效应时桩基的纵向振动特性,得出了桩顶导纳的解析解和桩顶速度时域响应的半解析解,并分析了相关参数对桩顶动力响应的影响,得到如下结论:
(1)对于大直径桩基,横向惯性效应对桩顶动力响应有着明显的影响:横向惯性效应会使桩顶速度时域响应曲线的振荡加剧,桩底反射信号的波谷值明显减小;在高频范围内,横向惯性效应会使桩顶复刚度的峰值减小,但在低频范围内,可以忽略横向惯性效应对桩顶复刚度的影响。
(2)忽略横向惯性效应的一维解只适用于细长桩。
(3)其他条件不变时,桩径的增大使桩底反射信号明显增强,反射波曲线的振荡明显加剧,桩顶导纳曲线的峰值增大,共振频率提前。在低频范围内,桩径的增大会使桩顶动刚度的衰减加快,会使桩顶动阻尼减小。
(4)其他参数不变时,随着饱和土中水的体积分数的增大,桩底反射信号幅值和桩顶导纳幅值均增大。在低频范围内,水的体积分数越大,桩顶动刚度越小,且衰减越快,桩顶动阻尼也越小。
[ 1 ] KESHAVARZ A, MALEKZADEH P, HOSSEINI A. Time domain dynamic analysis of floating piles under impact loads[J]. International Journal of Geomechanics, 2016, 17(2): 04016051.
[ 2 ] WANG K, WU W, ZHANG Z, et al. Vertical dynamic response of an inhomogeneous viscoelastic pile[J]. Computers and Geotechnics, 2010, 37(4): 536-544.
[ 3 ] 吴文兵, 王奎华, 窦斌. 任意层地基中黏弹性楔形桩纵向振动响应研究[J]. 振动与冲击, 2013, 32(8): 120-127.
WU Wenbing, WANG Kuihua, DOU Bin. Vertical dynamic response of a tapered pile embedded in layered foundation[J]. Journal of Vibration and Shock, 2013, 32(8): 120-127.
[ 4 ] ZENG X, RAJAPAKSE R. Dynamic axial load transfer from elastic bar to poroelastic medium[J]. Journal of Engineering Mechanics, 1999, 125(9): 1048-1055.
[ 5 ] WANG J H, LI Y L, QING B H, et al. Integral equation method for the dynamic responses of the pile-saturated-soil system to a moving load[J]. Geotechnical Special Publication, 2009, 27(186): 592-599.
[ 6 ] 李强, 王奎华, 谢康和. 饱和土中大直径嵌岩桩纵向振动特性研究[J]. 振动工程学报, 2006, 18(4): 500-505.
LI Qiang, WANG Kuihua, XIE Kanghe. Dynamic response for vertical vibration of large diameter pile in saturated soil[J]. Journal of Vibration Engineering, 2006, 18(4): 500-505.
[ 7 ] 杨骁, 蔡雪琼. 考虑横向效应饱和黏弹性土层中桩的纵向振动[J]. 岩土力学, 2011, 32(6): 1857-1863.
YANG Xiao, CAI Xueqiong. Vertical vibration of pile in saturated visco elastic soil layer considering transversal effects[J]. Rock and Soil Mechanics, 2011, 32(6): 1857-1863.
[ 8 ] 杨骁, 唐洁. 成层饱和土中考虑横向惯性的单桩纵向振动[J]. 岩土力学, 2013, 34(6): 1560-1566.
YANG Xiao, TANG Jie. Vertical vibration of single pile with transversal inertia effect in stratified saturated soil[J]. Rock and Soil Mechanics, 2013, 34(6): 1560-1566.
[ 9 ] 刘林超, 杨骁. 基于薄层法的饱和土桩纵向振动研究[J]. 岩土力学, 2010, 31(1): 92-98.
LIU Linchao, YANG Xiao. Study of longitudinal vibrations of pile in saturated soil based on layer method[J]. Rock and Soil Mechanics, 2010, 31(1): 92-98.
[10] 刘林超, 闫启方. 饱和土中管桩的纵向振动特性[J]. 水利学报, 2011, 42(3): 366-372.
LIU Linchao, YAN Qifang. Vertical vibration characteristics of pipe pile in saturated soil[J].Journal of Hydraulic Engineering, 2011, 42(3): 366-372.
[11] 张智卿, 王奎华, 李强, 等. 非饱和土中端承桩纵向振动问题简化解[J]. 工程力学, 2010,27 (5): 159-165.
ZHANG Zhiqing, WANG Kuihua, LI Qiang, et al. Simplified solution for vertical vibration of an end bearing pile embedded in unsaturated soil[J]. Engineering Mechanics, 2010,27 (5): 159-165.
[12] 王星华, 章敏. 非饱和土半空间中单桩竖向振动特性研究[J]. 岩土工程学报, 2013, 35(7): 1210-1220.
WANG Xinghua, ZHANG Min. Dynamical response of vertically loaded pile in an unsaturated porous media half-space[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1210-1220.
[13] NOVAK M, ABOUL-ELLA F, NOGAMI T. Dynamic soil reactions for plane strain case[J]. Journal of the Engineering Mechanics Division, 1978, 104(4): 953-959.
[14] 黎正根, 龚育龄. 波在大直径桩中传播的三维效应现象[J]. 岩石力学与工程学报, 1998, 17(4): 434-439.
LI Zhenggen,GONG Yuling. Discussion on three-dimensional effect of wave propagating in the pile with large diameter[J]. Chinese Journal of Rock Mechanics and Engineering,1998,17(4) : 434-439.
[15] LYSMER J, RICHART F E. Dynamic response of footings to vertical loading[J]. Journal of Soil Mechanics & Foundations Div, 1966,92(1): 65-91.
[16] 杨桂通, 张善元. 弹性动力学[M]. 北京: 中国铁道出版社, 1988: 240-242.
[17] 王奎华, 应宏伟. 广义 Voigt 土模型条件下桩的纵向振动响应与应用[J]. 固体力学学报, 2003, 24(3): 293-303.
WANG Kuihua, YANG Hongwei. Vertical vibration response and application of pile with general Voigt model[J]. Journal of Solid Mechanics, 2003, 24(3): 293-303.
