长期反复荷载作用对海上风电单桩基础的影响分析
2018-02-10马宏旺陈龙珠
马宏旺, 杨 峻,2, 陈龙珠
(1. 上海交通大学 船舶海洋与建筑工程学院土木工程系,上海 200240; 2. 香港大学 土木工程系,香港 薄扶林)
风能作为一种可再生新能源,近十多年在全球范围得到大力发展与建设。截止2015年底,全球风电累计装机容量已达到432.9 GW,并预计在2016~2020年间,风电增长率能保持近14.8%~11.2% 之间,在2020年底全球风电累计装机容量能达到792.1 GW[1]。目前风电主要以陆上风电为主,但随着陆上风能建设渐趋饱和,海上风能由于其固有的优势逐步成为风电发展的重要方向,截至2015年底,全球海上风电总装机容量达到12 GW。我国海上风电从2007年后得到快速的发展,截至2015年底已达到1 014.68 MW,目前还有2 307 MW海上风电正在建设中,1 240 MW 海上风电在待建中[2];规划到2020年,我国将开发建设有30 GW 海上风电。相比陆上风电,海上风力资源更为稳定、风速更高,且海上风电易于大型化,使得海上风电比陆上风电具有更高的效能。但另一方面,海洋环境下使得风电结构受力更为复杂,设计和建造难度加大,大大提高了风电建设的初期成本。另外,海上风电在设计使用期内长期承受波浪、潮流以及风荷载的反复作用,设计试验内一般反复作用的次数能达到约(~108)以上[3],在长期反复荷载作用后,结构整体自振频率和基础承载能力是否能够满足初期设计的需要,对海上风电结构设计安全性至关重要,是一个需要认真研究的课题。
Achums等[4]采用数值方法研究了砂土中单桩海上风电基础在长期反复荷载作用下的变形,研究表明在长期反复荷载作用下,随着反复荷载次数的增加,桩端位移会逐渐增加,建议在设计中要考虑长期反复荷载对桩变形的影响。但该研究采用了较复杂的数值模型,不利于直接进行工程设计。Domenico等[5]采用试验方法研究了长期反复荷载作用下单桩海上风电基础在黏性土中的变形,水平反复荷载次数为32 000~172 000次,研究表明长期反复荷载对桩的变形和整体风电结构自振频率都有一定的影响。张光建[6]基于无黏性土动三轴试验的基础上,建立土体刚度衰减模型,然后采用数值方法模拟了大直径钢桩在反复荷载作用下变形性能,并与室内模型试验结果进行对比,研究表明了长期反复荷载作用对桩变形的影响与荷载性质、桩长和桩径比以及土体参数有关。周济福等[7]在关于海上风电工程结构与地基的关键力学问题中指出长期循环载荷会导致地基土体强度衰减而可能引起地基破坏,需在设计中引起重视。
从工程实践和已有研究表明,对于海上风电结构,在设计时考虑长期反复荷载作用对其基础变形的影响是个十分重要的问题,也是个迫切需要解决的问题。本文就针对这个问题,采用 Cuéllar[8]基于模型试验提出的简化模型,以一工程案例为背景进行分析,定量研究长期反复荷载作用对桩基变形的影响。
1 长期反复荷载作用后海上风电数值模型
海上风电在整个设计使用期内承受风机荷载、波浪荷载以及风荷载等动荷载的长期反复作用,桩基础与桩周边土长期相互作用,Cuéllar采用模型试验对长期反复荷载作用下桩-土相互作用进行了研究,主要考虑砂性土。在研究基础上得出在反复荷载次数大于104后,桩周土变化可用一简化模型表示,见图1。 图1(a)显示了试验过程中,桩周土在长期反复荷载作用后,桩上部与土接触的部位,在一定范围土有所隆起,减少了桩的埋置深度;并把该现象用一简化的模型表示,见图1(b);桩上部形成一个倒圆锥状的空洞,最上部距离桩外壁距离为桩的直径,其深度采用公式(1)计算。通过土的材性试验研究表明,在反复荷载作用下,桩周边局部范围内土会变的会更密实,影响范围简化模型见图1(c)。

图1 长期反复荷载作用下桩周土变化简化模型Fig.1 Sketches of deformed soil around pile
图1中D是桩的直径(m),L是桩的长度,hs为反复荷载作用下减少桩的埋置深度,由下式计算:
(1)
(2)
式中:ΔVlong-term为长期荷载作用下桩周土的减少体积;ρ0是桩周土密度;ρmax是桩周土最大密度。
2 海上风电三维有限元模型
基于Cuéllar的研究成果,采用ABAQUS软件建立三维数值模型,见图2。模型包括风机叶片、轮觳和机舱(以集中质量设置于塔架顶端)、钢锥管塔架、连接段、钢桩、桩内土体、桩外土体和桩周边海水。连接段管壁厚度采用等效刚度确定,风机部位采刚体单元,集中质量按照风机类型放置于其质心位置。
桩周边海水以附加动水质量附加在相应的桩壁上,附加动水质量采用简化的Morrsion方法[10]计算。附加动水质量等效相同体积水的质量。由公式(3)计算每个节点等效附加水质量:
(3)
式中:j为与节点i相邻的节点;lij为单元有效长度;Ap为桩体相邻单元的面积;ρ为水的密度; 对于圆形桩体CM取2.0。

(a) 海上风电三维有限元模型

(b) 模型有限元与无限元区 图2 海上风电三维有限元模型和模型有限元与无限元区Fig.2 3D Finite element model of offshore wind turbine and finite element and infinite element zone
桩与内部填充土和外部土采用接触模型,ABAQUS软件在模拟桩-土接触时在计算模型的桩和土体上建立表面,定义出会相互接触的一对表面,采用单纯的主-从接触算法。为获得最佳的模拟结果,桩土表面,即主从面的选择必须遵守一些简单的原则:①从面应该网格划分更细的表面;②如果网格密度相近,从面应该采取较软材料的表面。基于这样的原则,在桩土相互作用中,将桩表面定为主接触面,土表面定义为从属接触面。 土体有限元模型见图2,采用无限单元模拟边界,桩周土体采用有限单元。无限元部分土体采用弹性模型,有限元部分土体采用Mohr-Coulomb模型。在本文研究中,为了进行对比分析,同时建立了不考虑长期荷载作用前海上风电三维数值模型,建模方法与上述方法一致。
3 数值模型侧向承载能力校核
Mohan等[11]在盐湖城地区进行的单桩水平载荷试验。单桩为内径0.305 m、壁厚9.5 mm的闭口钢管桩,桩长7.8 m,桩顶露出土面高度为0.4 m。混凝土弹性模量17 500 MPa,抗压强度20.7 MPa。由于在各级荷载作用下,钢筋及钢管应力都未达到屈服,故将钢材作为弹性材料,弹性模量最为2×105MPa,泊松比为0.25。
土层剖面如图3所示(图中长度单位是mm),土体采用摩尔库仑弹塑性模型,计算参数如下:(第一层砂土:摩擦角φ=20°,弹性模量E=6 MPa,c=10 kPa;第二层黏土:摩擦角φ=13°,弹性模量E=8.5 MPa,c=40 kPa;第三层砂土:摩擦角φ=25.5°,弹性模量E=11 MPa,c=15 kPa;第四层黏土:摩擦角φ=15°,弹性模量E=17 MPa,c=60 kPa;第五层砂土:摩擦角φ=35°,弹性模量E=38 MPa,c=15 kPa)。
桩顶水平荷载分级加载,分别为60 kN,120 kN和150 kN,每一级荷载下的桩顶位移试验值,见表1。采用上节中提到的建模分析方法:土体采用10 m×10 m×15 m(参考土体宽度大于20倍桩径,深度大于2倍的桩长),采用8结点四边形实体单元,钢桩采用壳单元,桩侧面与土之间采用接触单元,其摩擦因数取0.4。桩内部混凝土采8结点实体单元,不考虑其非线性。土体地面采用固定边界,四个侧面约束其法向变形。荷载作用于桩顶,在分析过程中,考虑了三种情况:
模型一:考虑桩-土相互作用,土体考虑弹性情况;
模型二:考虑桩-土相互作用,土体考虑非线性情况;
模型三:不考虑桩-土相互作用,桩土完全连接,土体考虑非线性情况。
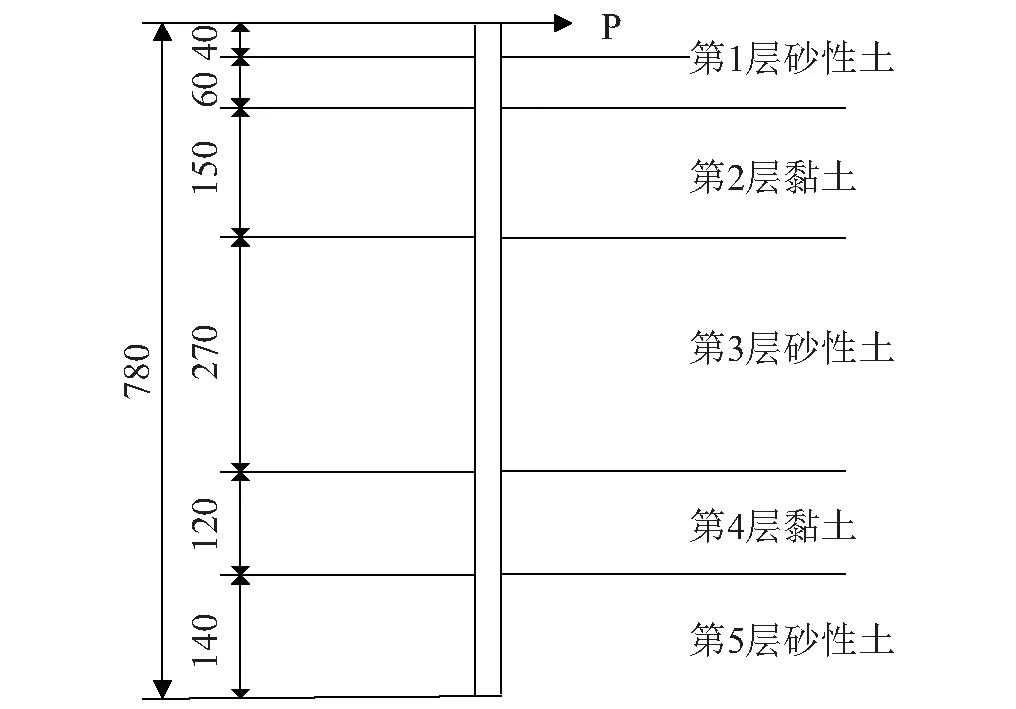
图3 分层土剖面图(mm)Fig.3 Soil profile in the field (mm)
分析结果见表1。从分析结果可以看出,考虑桩土摩擦相互作用和土的非线性与试验结果最接近,在加载初期误差较大,顶端位移误差达到近15%;随着荷载逐步加大,数值计算值和试验值误差在减小,基本处于10%以内,表明该模型能够较准确分析钢管桩在外力作用下的侧移反应,能够较真实模拟钢管桩在侧向荷载作用下的性能。而模型一把土体完全考虑成弹性在荷载较小时模拟结果与试验结果较接近,但随着荷载增大,数值模拟结果比试验结果逐步减小。模型三不考虑桩土相互作用,直接把桩土连接起来,在整个加载过程中,计算结果比试验结果都要小。

表1 桩顶位移试验值与各种情况计算值
4 分析实例
4.1 数值模型建立
在本文分析中,选取目前海上风电应用较多的3 MW风电机组。水深取10 m,轮嗀高度为90 m,桩入土深度为50 m,桩外径取6.0 m。风电机组总质量为1.546×105kg,叶片长度为54 m,每个叶片重8.4 t。桩、连接段和塔架的具体参数见图4。为了简化问题考虑地基为两层均质砂性土,土体基本参数见表2。塔筒内外的水以附加质量的方式附加在塔架上。塔架上施加自重荷载,风机重量以集中荷载形式作用于塔架顶端。在塔架顶端施加水平荷载1 300 kN模拟风机荷载,在平均海平面桩上施加波流荷载816 kN,在风机塔架上近似均布施加风荷载共318 kN,考虑极限承载力状态。在长期反复荷载作用下按照简化模型式(1)和式(2)计算hs时,需要有桩周砂土的初始密度和最大密度的比值,在本文里参考Cuéllar的研究成果,ρ0/ρmax≈0.82~1.0,hs≈0~12 m, 初步分析中取hs=6 m, 然后参数分析中考虑hs的深度对桩基础变形的影响。结构阻尼比取1%。三维整体数值模型见图5。
为对比分析,本文同时采用设计规范DNV[12]采用的非线性弹簧模拟桩周边土,弹簧的力与变形关系采用DNV给出的p-y曲线关系:
(4)
式中:p是泥面下深度Z处作用于桩上的水平抗力值;y是泥面下深度Z处桩的水平位移;A是荷载类型系数,考虑长期反复荷载取0.9;pu是泥面下深度Z处桩侧单位面积极限水平抗力标准值, 计算参考DNV规范附录F.2[12];k是土抗力初始模量。

表2 土材料参数
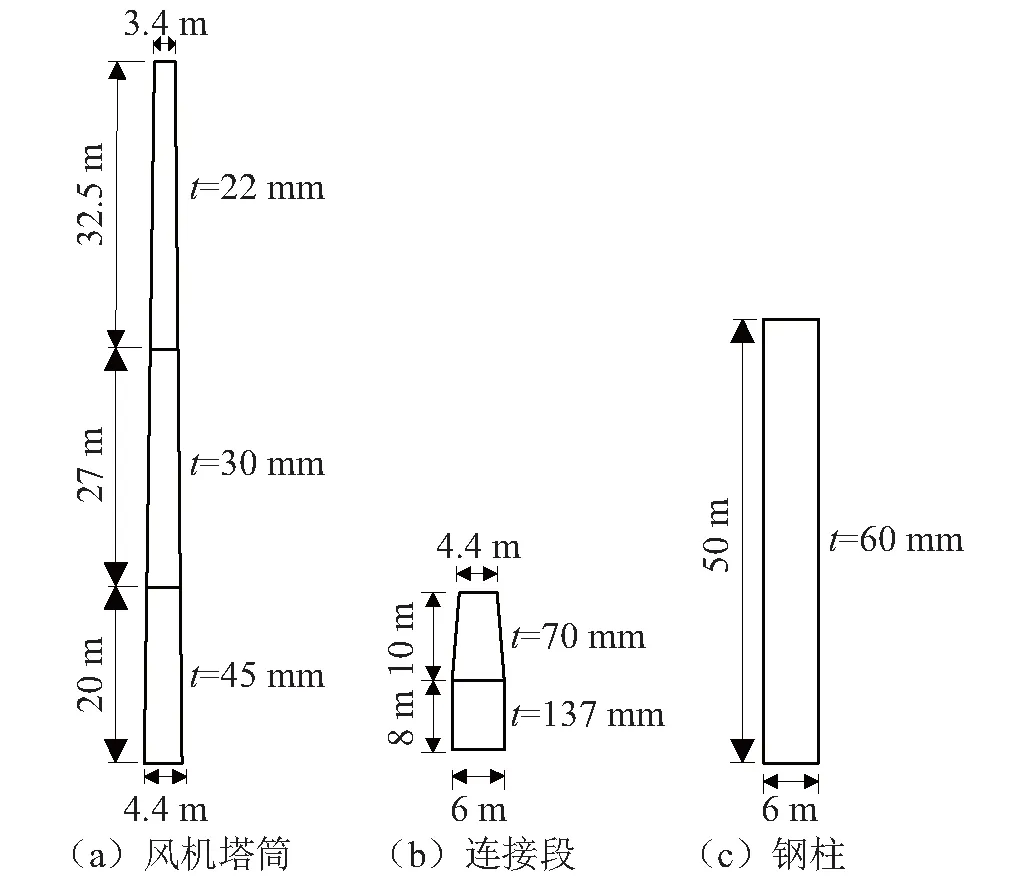
图4 塔架、连接段和桩的几何尺寸和壁厚Fig.4 Dimension and thickness of tower
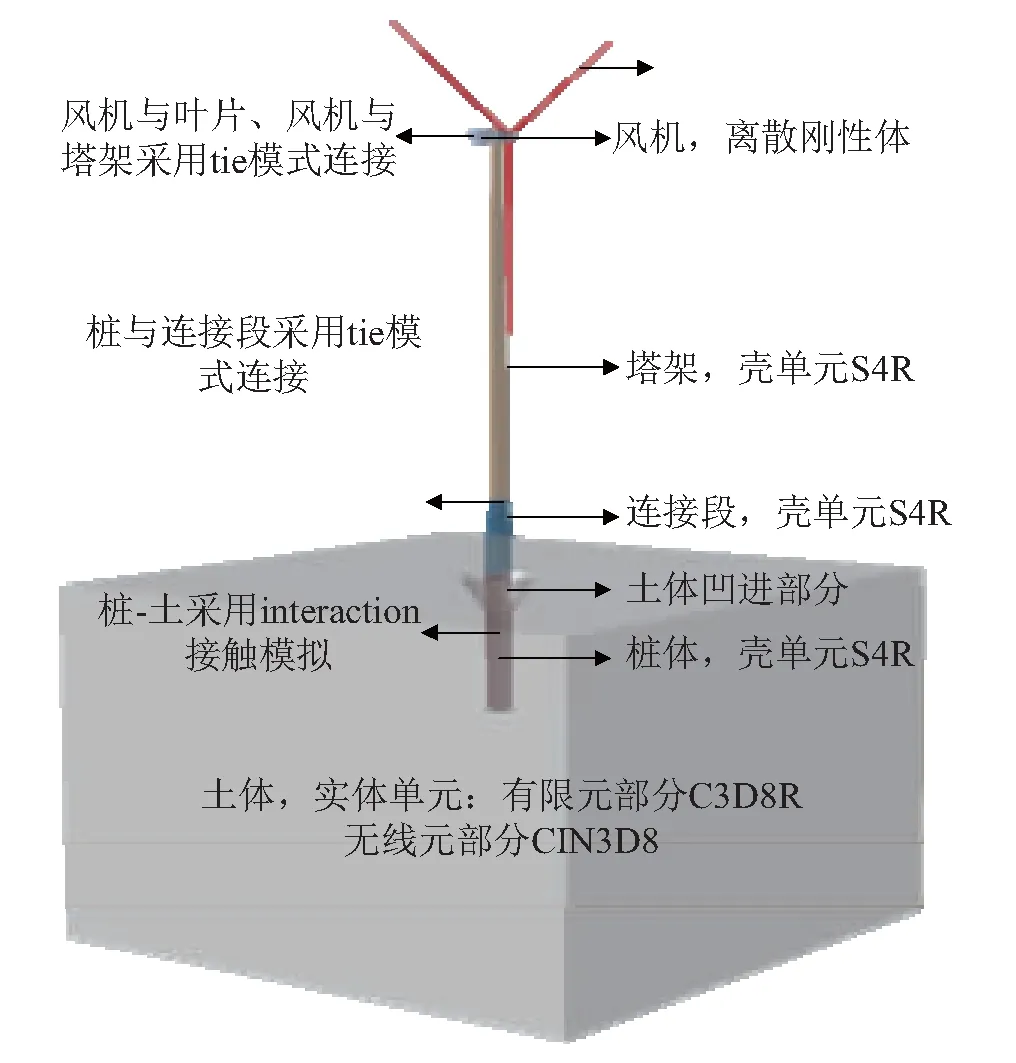
图5 3 MW海上风电三维有限元模型Fig.5 Threes dimension FEM model of 3 MW wind turbine
4.2 分析结果
在建立了海上风电三维数值模型后,具体分析步骤为:第一步进行地应力平衡;第二步施加各单元的自重荷载;第三步在塔架底部施加一固定位移;第四步释放固定位移进行自由振动分析,并采取塔架顶端位移(见图6);然后在风机顶端、塔架以及海水对应部分施加水平荷载。
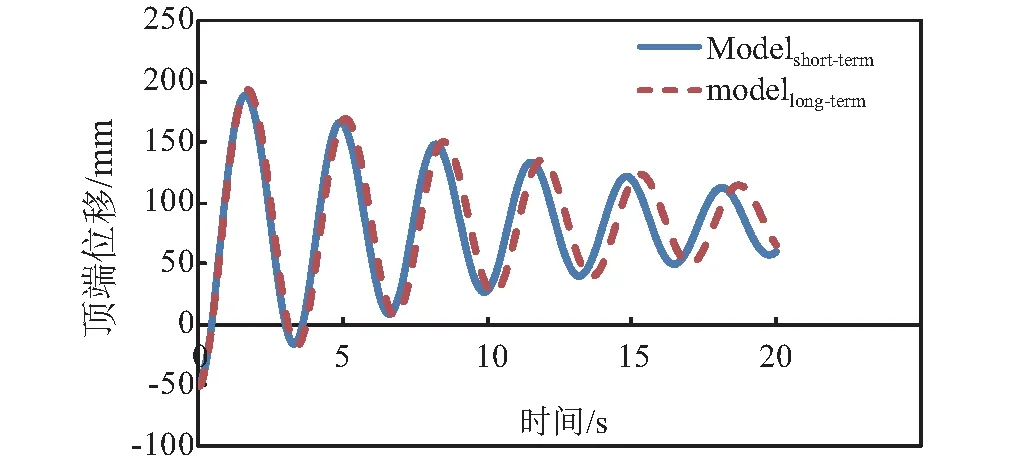
图6 两种模型塔架顶端自由振动位移时程Fig.6 Tower top displacement of two models
在施加了重力荷载和侧向水平荷载后,风电塔架、连接段和桩最大应力出现在塔架中下部。图7(a)给出在考虑长期荷载反复作用下桩周边土体的水平变形,可以明显看出,土体变形主要集中在桩-土接触的上半部分,桩体下面部分变形较小。图7(b)给出了没有考虑长期荷载作用后水平荷载作用后土体的水平变形,与图7(a)相似,变形主要发生在桩上部20 m的区域,土体变形略有减小。图8给出考虑和不考虑长期反复荷载作用下,桩-连接段在侧向力作用下水平变形,可以看出两者变形基本一致,考虑长期荷载作用后,连接段的水平变形较未考虑长期荷载作用的要大一些。
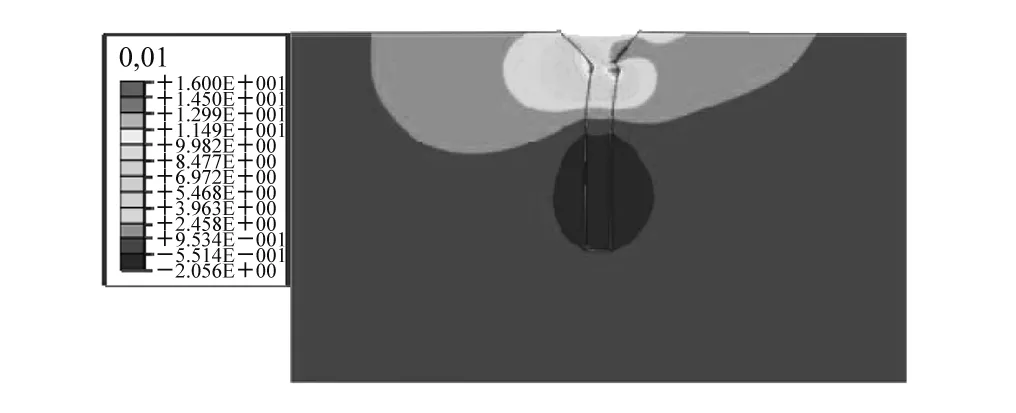
(a) 考虑长期反复荷载作用土体变形

(b) 未考虑长期反复荷载作用土体变形图7 考虑长期反复荷载作用土体变形和未考虑长期反复荷载作用土体变形Fig.7 Soil deflection under long-term loading and soil deflection without long-term loading
表3列出了考虑反复荷载长期作用后和未考虑反复荷载长期作用海上风电第一自振频率和塔筒底部水平位移和转角以及泥面处桩的水平位移和转角。两个模型分别表示为ModelLong-term和Modelshort-term。从表3可以看出,经过长期反复荷载作用后,风电结构第一自振频率降低了约6.25%,单纯从数值上看不是很大,但是考虑海上风电设计中,第一自振频率允许的范围为0.21~0.33 Hz,处于一个较小的区间,故第一自振频率降低6.25%是个不容忽视的影响,容易使结构第一自振频率落入共振区间。在长期反复荷载作用后,塔筒底部水平位移增加了近30%,泥面处水平位移增加了近48%;泥面处桩转角位移增加了28.4%,塔筒底部转角增加了14.6%。从以上结果可见,长期反复荷载作用后,对桩的水平位移和转角都有较大影响,这些变形增加不仅会影响风电结构的正常运行,同时可能影响结构整体安全性,在设计初期必须予以考虑。
表3中给出了采用规范方法计算的结构整体自振频率、桩端位移和转角。从表3中可以看出,按照规范计算的结构自振频率与三维有限元模型计算结果相差不大,而按照规范计算的桩泥面处位移和转角比按照有限元模型计算的结果要小很多,从而表明按照现行规范提出p-y方法分析大直径桩的侧向变形还要进行更为详细的论证。
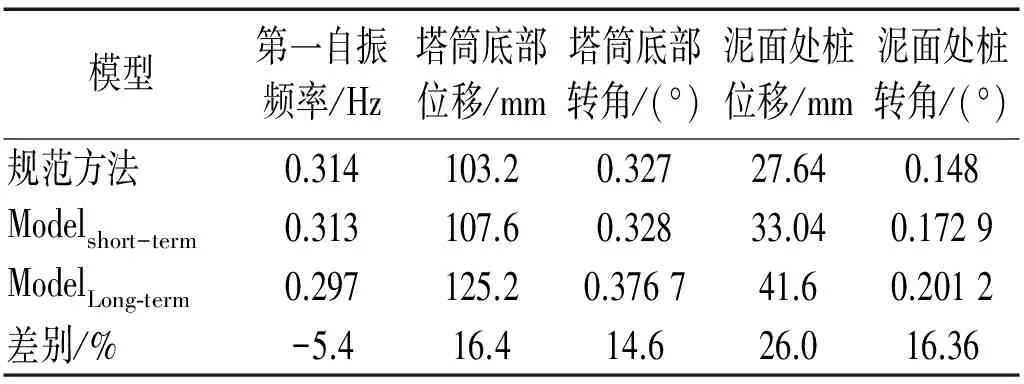
表3 海上风机结构第一自振频率和变形
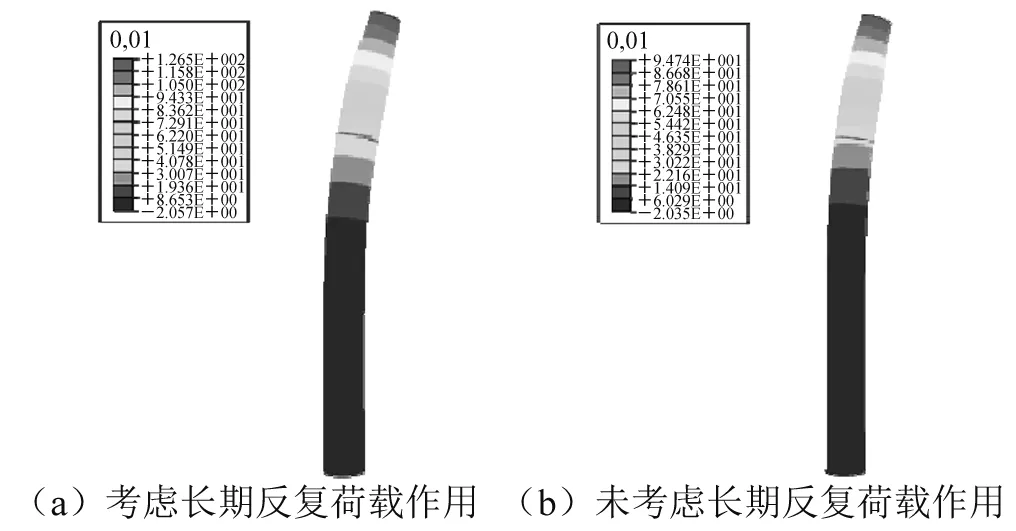
图8 桩-连接段变形Fig.8 Deflection of pile and transition piece
5 参数分析
5.1 桩周土减少深度的影响
根据式(1)和(2)可知,桩周土减少深度与土体初始密度和最大密度有关,考虑土体初始密度的不确定性以及可能出现的不利情况,本文在下面分析桩周土减少深度为6 m、8 m、10 m和12 m情况下风电结构第一自振频率和桩的变形,见表4。从表4可以看出,减少深度由6 m增加到12 m后,也就是增加到近2倍的桩径后,第一自振频率降低约3.7%。塔筒底部水平位移增加约36.0%,泥面处水平位移增加约58.6%,塔筒底部转角增加了约35.5%,泥面处桩转角增加约31.7%。从分析结果可以看出,桩周土减少深度的增加,也就是减少桩的埋置深度后,一定范围内对风电结构第一自振频率影响相对不大,但是对桩水平位移和桩端转角有较明显的影响,在海上风机基础设计中需认真对待。
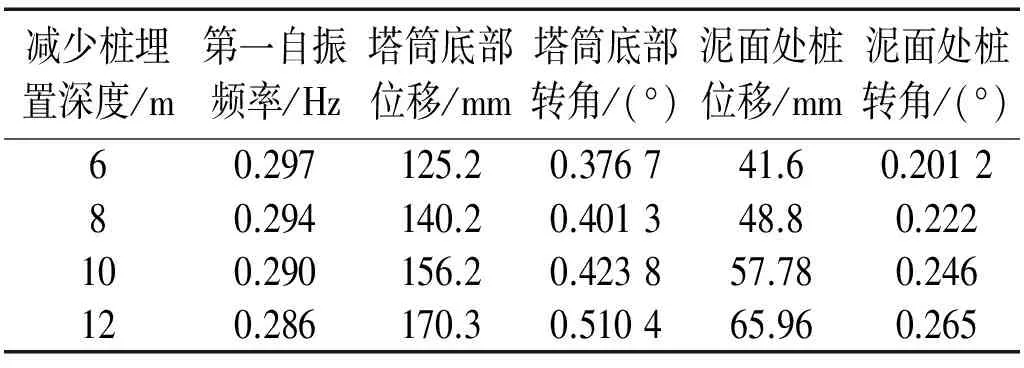
表4 桩周土减少深度对第一自振频率和桩变形的影响
5.2 桩周土弹性模量变化对桩变形影响
根据Cuéllar的研究结论,在反复荷载作用后,桩周一定范围的土有变密实的趋势,土密实后,不仅密度有所增加,弹性模量也会随着增加。考虑到土弹性模量的不确定性,图9(a)给出了桩周土弹性模量变化对塔筒底部水平位移和泥面处水平位移的影响,可以看出随着桩周土弹性模量的增加,两者都有明显的下降。且在弹性模量较小的范围内下降较为明显。图9(b)给出桩周土弹性模量对塔筒底部转角和泥面处桩转角的影响,可以看出,两者都有一定程度的下降。
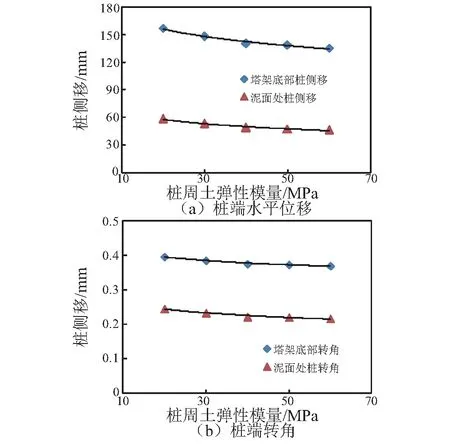
图9 桩周土弹性模量对桩变形的影响Fig.9 Soil Young’s modulus Vs pile’s deformation
6 结 语
海上风电在设计使用期内,长期承受风机荷载、波浪荷载和风荷载的反复作用,桩与周边土也长期相互反复作用,风机结构整体动力特性以及桩基础的承载能力在反复荷载作用后究竟会产生什么样的变化,对于保证海上风电结构在整个设计使用期的安全性至关重要,是个必须予以考虑的问题。
本文研究采用Cuéllar提出的简化模型,建立三维有限元模型,考虑桩-土相互作用,土的非线性以及海水的影响,采用自由振动确定海上风电第一自振频率;通过近似加载极限状态荷载分析桩基础结构水平变形。分析研究表明,在长期反复荷载作用后,风电结构第一自振频率降低了约5.5%,塔筒底部水平位增加了近16.4%,泥面处水平位移增加了近26%;泥面处桩转角位移增加了16.4%,塔筒底部转角增加了14.6%。由此可见,长期反复荷载作用后,对风电结构第一自振频率有明显的影响,考虑到风机第一自振频率设计中要求处于一个较窄的范围,这个影响不容忽视。长期反复荷载作用后,对桩的水平位移和转角都有较大的影响,这些变形增加不仅会影响风电结构的正常运行,同时可能影响结构的整体安全性,故在设计初期必须予以考虑。
由于在海上风电结构设计中,存在大量不确定因素,为了更加全面考虑长期反复荷载作用对海上风电结构整体自振频率和桩变形的影响,研究将在以后工作中进一步深化。
[ 1 ] Globe Wind Report, Annual Market Update[R]. Global Wind Energy Council, 2015.
[ 2 ] 文锋. 我国海上风电现状与分析 [J]. 新能源进展,2016, 4(2): 152-158.
WEN Feng. Developments and characteristics of offshore wind farms in China [J]. Advances in New and Renewable Energy, 2016, 4(2): 152-158.
[ 3 ] SCHAUMANN P, LOCHTE-HOLTGREVEN S, STEPPELER S. Special fatigue aspects in support structures of offshore wind turbines [J]. Materials Science and Engineering Technology, 2011, 42(12): 1075-1081.
[ 4 ] ACHMUS M, KUO Y S, ABDEL-RAHMAN K. Behavior of monopile foundations under cyclic lateral load [J]. Computes and Geotechnics, 2009,36: 725-735.
[ 5 ] DOMENICO L, SUBHAMOY B, DAVID M W. Dynamic soil-structure of monopile supported wind turbines in cohesive soil [J]. Soil Dynamics and Earthquake Engineering, 2013,49: 165-180.
[ 6 ] 张光建.长期水平循环荷载下大直径桩的累积位移分析[D]. 杭州:浙江大学,2013.
[ 7 ] 周济福,林毅峰. 海上风电工程结构与地基的关键力学问题 [J]. 中国科学:物理学 力学 天文学,2013,43(12): 1589-1601.
ZHOU Jifu, LIN Yifeng. Essential mechanics issues of offshore wind power systems [J]. Science China: Physica, Mechanica & Astronomica, 2013, 43(12): 1589-1601.
[ 8 ] CUÉLLAR P. Pile foundations for offshore wind turbines: numerical and experimental investigations on the behaviour under short-term and long-term cyclic loading [ D]. Von der Fakultät VI-Planen Bauen Umwelt der Technischen Universität Berlin, 2011.
[ 9 ] 王金昌,陈页开. ABAQUS在土木工程中的应用[M]. 杭州:浙江大学出版社,2006
[10] MORISON J R, BRIEN O, JOHNSON M P. The force exerted by surface waves on piles [J]. Transaction of American Institute of Mining and Metallurgical Engineers, 1950,189: 149-154
[11] MOHAN D, SHRIVASTAVA S P. Nonlinear behaviour of single vertical pile under lateral loads [C]//Proceedings of the 3rd Annual Offshore Technology Conference (Vol 2, PaperOTC1485). Houston, 1971: 677-686.
