节点电压向量法在计量检定工作中的应用

韩越

摘要：随着科学技术的发展，各种电学设备日新月异，其计量检定工作也越来越复杂。计量检定的精准度直接关系着电学设备的后期使用，本文提出了一种基于节点电压向量的故障诊断方式，从而实现故障的快速定位。

Abstract： With the development of science and technology， a variety of electrical equipment changes every day. The measurement verification work is becoming more and more complex. The accuracy of measurement verification is directly related to the later use of electrical equipment. In this paper， a fault diagnosis method based on node-voltage vector is proposed to realize fault location rapidly.

关键词：故障诊断；节点电压向量 ；数据处理；计量检定

Key words： fault diagnosis；node-voltage vector；data processing；metrological verification

中图分类号：TH71 文献标识码：A 文章编号：1006-4311（2017）35-0207-03

0 引言

目前，我国企业对电学设备的需求越来越大，各种电学设备在人们生产生活中的影响也逐渐增强，为了确保电学设备的正常运行和使用，就要定期对其进行计量检定。在计量检定工作中，必然会发现设备的一些故障，在影响检测结果精确性的同时，也会使设备的后期使用出现相关问题。所以，在计量检定工作中发现设备故障后，能快速地实现对故障的诊断和定位，显得非常重要。

1 电学设备的故障分类

电学设备的核心部件是各种电路元件，电路故障类别繁多。按照某一时段故障是否只有一种分为多故障和单故障，单故障的诊断比多故障诊断要简单很多，但实际上多故障也是由多种单故障组成的，因此很多时候是可以用单故障的诊断方法来处理多故障问题的。依据故障和损坏的严重程度可以分为软故障和硬故障，硬故障通常是元件数值发生偏差情况非常严重，结果将造成灾难性的的电路系统故障，软故障则是当电路元件出现老化变质等原因时，其参数数值就会超过容差允许的范围，从而造成故障的出现。硬故障可以看作是软故障的某种极限形式，元件出现开路的情况可以看作是软故障的极大值，出现短路的情况可以看作是极小值[1]。因此，大多数针对系统软故障的处理方法在硬故障领域也都是适用的。图1是发生故障时电路性能参数变化图。

从图1可以看出，元件参数在标称值上下浮动10%是正常范圍，大于10倍或小于0.1倍的标称值时可以认定电路发生硬故障，其余情况可以认为是软故障。

2 直流激励下的故障定位

本文主要是研究电路的单、软故障，为了方便对节点电压向量提取法的研究，本文以该方法在电路的单、硬故障中的应用为例来说明，如图2所示为某电学设备内二阶RC低通滤波电路[2]。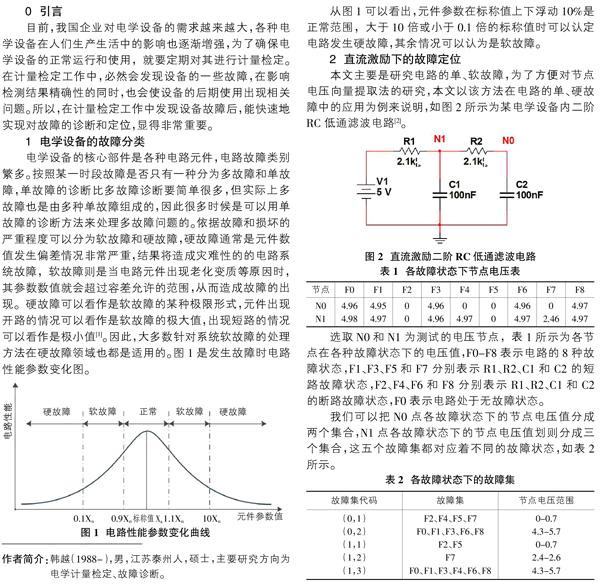

选取N0和N1为测试的电压节点，表1所示为各节点在各种故障状态下的电压值，F0-F8表示电路的8种故障状态，F1、F3、F5和F7分别表示R1、R2、C1和C2的短路故障状态，F2、F4、F6和F8分别表示R1、R2、C1和C2的断路故障状态，F0表示电路处于无故障状态。

我们可以把N0点各故障状态下的节点电压值分成两个集合，N1点各故障状态下的节点电压值划则分成三个集合，这五个故障集都对应着不同的故障状态，如表2所示。

从表3中我们可以很明显的区分出F4故障（R2断路）和F7故障（C2短路），但是其他的故障就无法通过这种简单的方法来确定，因此，故障诊断率仅仅是25%。

3 交流激励下的故障定位

虽然使用直流激励来寻找故障集交集的方法简单易行，但是不能适用于其他多数电路，特别是那些含电容元件的模拟电路[3]。进一步研究，如图3所示，RC低通滤波电路的激励源是正弦激励。

表5中，除了F2和F5故障，其他故障都可以明显的被诊断出来，可以看出，对电路施加了正弦激励后，节点电压值和施加直流激励时的区别很大。通过对多节点电压幅值和相角的提取，就可以准确诊断出75%的故障。

4 结束语

节点电压向量法是直流节点电压法故障诊断方法的扩展和延伸。在电学计量检定工作中，如果发现所测数据误差较大，可以采用此方法进行快速故障定位，方便易行。但是，本方法也存在一定的局限性，在数字电路元件比较多的电学设备中的应用还需要进一步研究。

参考文献：

[1]朱大奇.电子设备故障诊断原理与实践[M].电子工业出版社，2004：1-20.

[2]Miche Y， Van Heeswijk M， Bas P， Simula O， Lendassc A. TROP-ELM： A double-regularized ELM using LARS and Tikhonov regularization[J]. Neurocomputing， 2011，74： 2413-2421.

[3]何宏华.电压电流相序对电能测量影响的研究[J].电子世界，2013（10）：213-215.

[4]张庆辉，崔勇，朱亚峰.基于DSP的谐波电能计量算法研究[J].电测与仪表，2014，51（6）：9-13.

[5]付华.基于极限学习机的半监督分类[D].西安电子科技大学，2013.endprint