基于禁忌搜索算法的改进有向赋权网络最短路径算法

罗亦俊,刘小亮

(1.兰州交通大学 交通运输学院，甘肃 兰州 730070;2.西安科技大学 通信与信息工程学院，陕西 西安 710054)

作为网络优化设计中的关键问题，最短路径(Shortest Path ,SP)问题在求解通信网、交通网、电网以及项目运筹网等网络规划和路径决策中有着重要意义[1]。通常情况下，经典的最短路径问题仅仅考虑路径的距离最短、时间最短或者费用最少，属于单目标优化，这就很难准确描述实际网络环境中的问题。在实际网络优化问题中的最短路径问题经常会和多目标或多约束条件关联到一起[2]。如通信网络中的时延、分组掉包、带宽、抖动等约束条件，在多条件最短路径问题中，往往并非某一条件的最优解可以包揽这个多目标条件的最优解，因而针对某一目标取得较优解[3]。

作为网络优化设计中的关键问题，最短路径(Shortest Path ,SP)问题在求解通信网、交通网、电网以及项目运筹网等网络规划和路径决策中有着重要意义[1]。通常情况下，经典的最短路径问题仅仅考虑路径的距离最短、时间最短或者费用最少，属于单目标优化，这就很难准确描述实际网络环境中的问题。在实际网络优化问题中的最短路径问题经常会和多目标或多约束条件关联到一起[2]。如通信网络中的时延、分组掉包、带宽、抖动等约束条件，在多条件最短路径问题中，往往并非某一条件的最优解可以包揽这个多目标条件的最优解，因而针对某一目标取得较优解[3]。

基于上述几点，本文提出一种基于禁忌搜索算法的改进有向赋权网络最短路径的计算方法，此方法的目的是缩减计算有向赋权网络最短路径模型问题的时间和次数，提高计算效率。

1 有向赋权网络最短路径问题模型描述

本文基于现实通信和交通网络基础，构建一个有向赋权网络的最短路径问题模型，该模型可以被描述成一个连通图G=(V，E)。其中V(|V|=n)为结点集合，vi∈V是图G的一个顶点，表示通信网络中的路由器或者交通网络中的道路交叉口等；在图G=G(V，E)中，eij∈E是图G中的一条边，eij是vi到vj的一条道路或者一条链路。每条边都赋有一个实数wij，表示实际网路中的距离，用邻接矩阵distance存放图G各结点对之间的特性，当一个结点不能直接到达另一个结点时，将其wij设定为一个无穷大的数。从起点出发到达终点距离最短的那条路径就为图G的最短路径。

1)邻点

2)解的表示：给每一个顶点一个优先权(不同的顶点权不同)。

3)顶点：v1，v2,…，vn。

4)优先权：P(vi)=i，是指vi优先权的值为i。令P(v1)=1，…,P(vn)=n。

5)邻域搜索：随机选择若干顶点对，交换每对顶点的优先权。

6)解码：从原点开始，v1开始找到-(v)中优先权最大的点v′，令v=v′，如此下去，直到v′=n(终点)。

其中，从v1到vn节点的路径Path1->n由路径经过的节点序列构成：Path1->n=v1->vi->vj…vk->vn。

路径的长度计算结果为Length1->n=w1,i(distance(1,i))+wi,j(distance(i,j))+…+wk,n(distance(k,n))。而该模型问题的最短路径可以转化成求Length1->n的最小值，即Min(Length1->n)=min(∑wij)。在该过程中，针对该模型与其他模型不同处是有向以及带权值，其中权值的用法主要是对领域解的确定。

2 应用TS算法求解设计思路

禁忌搜索(tabusearch TS)模拟人脑短期记忆功能，全局逐步寻找最优解，为避免无效的循环计算，它使用禁忌准则来实现。同时使用藐视准则来接受较差解，用来确保对于不同范围内有效路径的探测，在这方面禁忌搜索的局部搜索能力较强。

本文设计的有向赋权网络问题的禁忌算法，首先设计一个合理的邻接矩阵方法，根据起点获取下一个可能到达的点的集合，然后在该集合中随机取出其中一个有效点作为路径达到的第二个点，依次循环获取，直至达到终点位置结束，获取的所有点的集合称为初始解，然后计算其长度，再根据领域搜索原则，获取领域解，据此获取局部最优解，最后加入到禁忌表中。当整个运算达到了某一规则后，停止搜索，根据禁忌表原则获取其最短路径。

该算法求解的设计思路主要包括以下6个部分。

1)领域：变换初始路径中随机选取点的优先权，通过解码原则获取下一个点的位置，产生新的路径集合称为初始路径领域。为更好地获取有效领域路径，本文采用了递归法，通过多次递归获取领域路径。

2)候选解集：初始路径的邻域子集。

3)禁忌表：用来存放禁忌对象的数据结构。通常情况下，禁忌表中的对象是不能被选作产生邻域的新解，这也是为了防止出现陷入局部最优解和循环搜索的情况。

4)藐视准则：如果候选解集中的最优对象比以前历史最优解更优时，就算该对象已经被禁忌，但仍可以替代之前的最优解，在下一次迭代过程作为初始解， 也就是特赦该禁忌对象。还有一种特赦情况是：如果候选解集中的全部对象都已经被禁忌，那么特赦最优候选解。

5)终止条件：如果算法已经达到之前预设的迭代次数，或者在设置好的固定周期内连续获得的最优解不发生变化，这两种情况满足其中一个就可以终止计算过程，将固定周期设置成算法总迭代次数的0.6倍。

3 算法的实现过程

本文提出的关于有向赋权网络最短路径问题模型的解决方法，其具体实现流程如图1所示。

在搜索过程中，由于有向赋权网络路径是路径固定的不可随机抽点，在本文中，主要采用多次递归函数方法结合邻接矩阵的特性获取迭代初始解。通过计算迭代初始解的长度，并将迭代初始解的路径编码放入禁忌表中，然后根据权限值的大小选取该初始解的路径领域解，选取出符合条件的领域解集后，对其领域解集进行路径长度计算，通过比较该领域解集与迭代初始解之间的路径长度，确定下一轮迭代初始解和禁忌表是否添加和解禁。一次轮询比较，直到终止条件得到满足，结束此次计算。以上是本文设计实现思路。

初始解的确定设计：根据模型要求得到源节点和目标节点的编码，根据源点及上面的邻接矩阵判断与该源点连通的其他节点编码，从中取出权值最大的点，依次类推获取最后的目标节点。

图1 算法实现流程

评价函数的设计：分别计算每一次领域搜索后获取的最短路径编码长度，判断该路径是否加入到禁忌表中，等待预设的迭代次数结束后，计算禁忌表中距离最短的路径作为该有向拓扑网络的最短路径。

在本文设计中增加了一个条件函数用于处理同一禁忌长度和同一迭代次数，在不同领域路径搜索数目下，计算出最短路径编码的出现率关系。每个领域路径搜索数目的最短路径编码出现率计算方法如式(1)所示

(1)

式中：Wm为最短路径出现率，C为运行次数，tempCount为最短路径出现次数。

终止条件的设计：算法达到预设的迭代次数，即可终止计算过程。

4 试验与结论

本文给定一个具体模型，其中包含的点数为20个，其有向赋权如图2所示。

在上述的有向赋权图中，圆圈中的标号代表路径编码，同时也表示上一个节点到下一个节点的权值，而带箭头的线上的标号表示两点间的长度。

为解决该模型的问题，本文利用java语言在eclipse软件工具中编程，完成1->20的最短路径查找。

整个程序中采用的路径编码策略：采用可变长，将节点序号作为路径的编码方式，每条路径都

图2 有向赋权拓扑结构网络

由起始节点1到目的节点号编码串表示，其中所有编码均采用List(链表结构)实现。编码串所代表的路径不能有重复节点，同时不允许出现无连接节点间的编码关系。

禁忌算法参数设置：终止迭代次数=10，禁忌长度为1-19，领域解集大小分别取3、5、9，运行次数=1 100；通过编写运行程序后发现其最短路径为1->4->10->12->14->17->18->20；

长度为15，运行1 100次出现该路径的次数情况如图3所示。

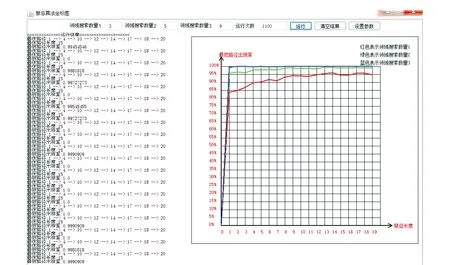
图3 运行结果

由图3可以得知：上述模型所得的编码路径1->4->10->12->14->17->18->20为最短路径的编码串，其最短距离为15。

本文另外设计一个8个点的模型，根据以上算法的设计、实现以及运行的结果，可充分证明本文提出的关于有向赋权网络最短路径问题的解决方法是有效的，同时，确定了一种对领域搜索数目的设置确定方法。

在后续的工作中，需要进一步研究算法的时间复杂度，并对算法进行改进，引入其他优秀的算法(比如遗传算法)来减少其时间复杂度。

[1] 阎啸天，武穆清.基于GA的网络最短路径多目标优化算法研究[J].控制与决策，2009,24(7):1104-1109.

[2] 郝光，张殿业，冯勋省.多目标最短路径模型及算法[J].西南交通大学学报，2007,42(5):641-646.

[3] 朱涛，张水平，郭戎萧，等.改进的加权复杂网络节点重要度评估的收缩方法[J].系统工程与电子技术，2009，31(8):1902-1905.

[4] 张帆，李军，王钧，等.多目标最短路径进化求解方法[J].系统工程，2005,23(9):123-126.

[5] 康晓军，王茂才.基于遗传算法的最短路径问题求解[J].计算机工程与应用，2008,44(23):22-23.

[6] 冶晓隆，兰巨龙，郭通．基于主成分分析禁忌搜索和决策树分类的异常流量检测方法[J]．计算机应用，2013,33(10):2846-2850.

[7] 李进，傅培华，李修琳，等.低碳环境下的车辆路径问题及禁忌搜索算法研究[J].中国管理科学，2015,30(10):1003-207.

[8] 黄艺坤.Dijkstra 算法在室内移动导航最短路径寻址的改进[J].福建师范大学学报(自然科学版),2017,33(5):1000-5277.

[9] 胡天寒，叶明全，张浩，等.基于禁忌搜索算法的特征选择方法研究[J].2016,18(5):1673-1749.

[10] 梅海涛，王毅，华继学．直觉模糊小生境的自适应遗传算法求解旅行商问题[J]．计算机科学，2016,43(11) :46-49．

[11] 张毅，梁艳春.基于选路优化的改进蚁群算法[J].计算机工程与应用, 2007, 43(2):60-63.

[12] 钟石泉,杜纲,贺国光.有时间窗的开放式车辆路径问题及其遗传算法[J].计算机工程与应用,2006，34:201-2-4.

[13] 於世为,郭海湘,诸克军.基于 GA-TS 的开放式车辆路径优化算法及应用[J].系统管理学报 ,2012，264-269.

[14] 李茂军, 童调生.单亲遗传算法及其全局收敛性分析[J].自动化学报, 1999,25(1): 68-72.

[15] 李惠,蒋大奎.基于单亲遗传禁忌搜索算法的手术排程问题研究[J].计算机应用研究,2013,699-702.