运动滑板数学模型的建立及动力学分析

胡仕成 曾 强 熊豪利

（1.中南大学机电工程学院，湖南长沙410000；2.高性能复杂制造国家重点实验室，湖南长沙410000）

0 引言

滑板运动起源于冲浪运动，第一块滑板诞生于19世纪50年代。常见滑板由一块板、两个支架、两个基座和四个轮组成，支架与基座连接，固定在车板上，支架基座组件是滑板最重要的结构部件[1]，如图1所示。

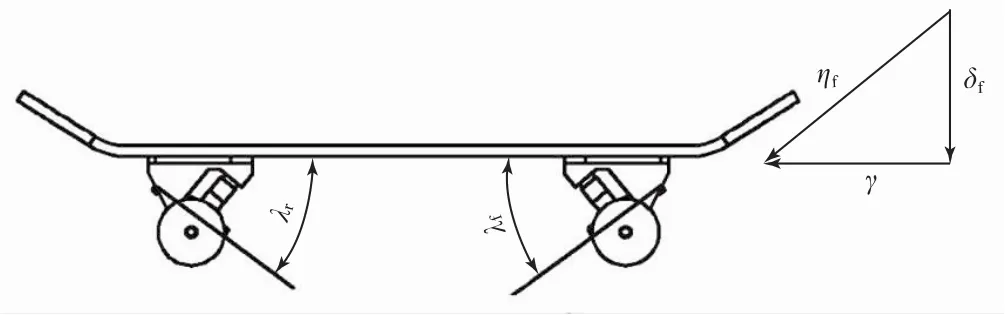
图1 滑板二维正视图

20世纪70年代末80年代初，M.Hubbard[2-3]提出了滑手在滑板上运动的数学模型，运用动力学的基本定理，得出模型的运动方程。A.S.Kuleshov[4]在M.Hubbard提出的模型基础上进一步分析，使用Gibbs-Appell形式的运动方程得到滑板运动的数学模型。本文利用ADAMS软件建立滑板刚柔耦合模型，进行运动学分析，测量板面倾斜角度与车轮旋转角度，代入数学模型，验证动力学模型的可行性。

1 数学模型的建立

假设滑手在整个运动过程中，板面倾斜角度为γ，引入OXYZ固定坐标系，O为原点，位于平面的某个点上，轴线OZ引导为垂直于运动平面；线段AB由其中心坐标X和Y确定，角度θ由该线段和固定轴OX确定；当板倾斜角度γ时，前轴顺时针旋转角度δf，同时后轴逆时针旋转角度δr，如图2、图3、图4所示，那么：

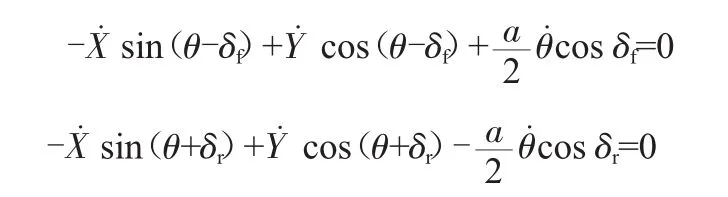
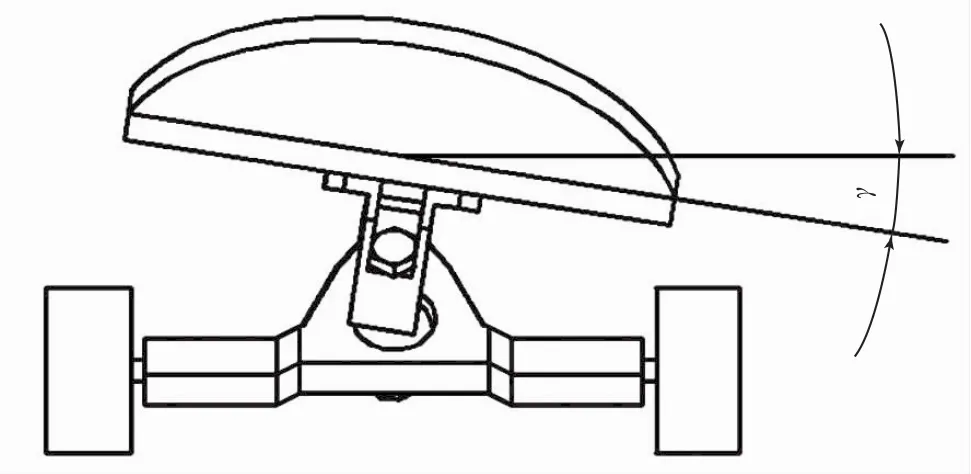
图2 滑板板面倾斜示意图

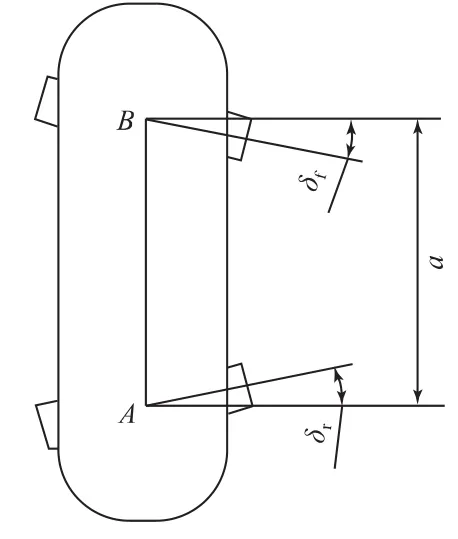
图3 滑板各轮轴偏转示意图

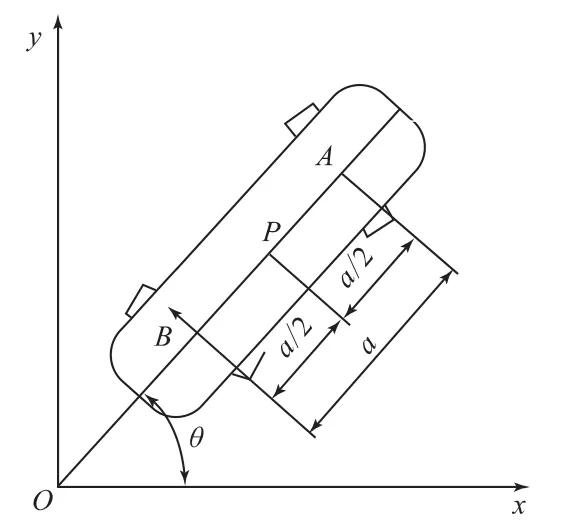
图4 滑板0xy坐标系

推导将滑板倾斜度和轴线转动角度关联起来的公式，引用微量旋转理论，考虑滑板前轴围绕倾斜轴线的微量旋转ηf；轴线围绕矢量e1转动角度-γ，围绕矢量转动角度-δf；得：

2 动力学模型的建立

2.1 滑板虚拟样机的建立

利用三维建模软件SolidWorks建立滑板各零件的实体模型，然后进行无干涉装配，导入ADAMS，该系统需要添加的约束分别为：（1）滑板板面与基座固定；（2）两侧螺杆头与基座固定；（3）滑板支架顶部半球与基座采用圆柱副；（4）螺杆与螺帽固定；（5）滑板支架与轮子采用旋转副。建立的滑板虚拟样机如图5所示。

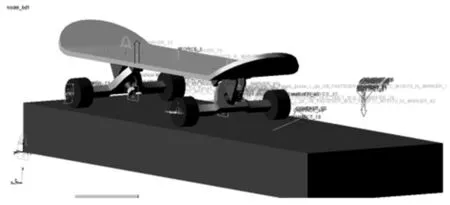
图5 滑板虚拟样机

2.2 基于ADAMS与ANSYS柔性体联合仿真

ADAMS/Flex模块允许在ADAMS模型中根据模态频率数据创建柔性体部件[5-6]。PU垫材料为氯丁橡胶，其材料属性定义如下：弹性模量E=1.5e6 Pa，泊松比μ=0.49，密度ρ=1.25 kg/m3。单元类型：solid185，对其进行网格划分。根据实际接触，建立主节点与刚性区域，生成MNF文件[7]，导入ADAMS。

2.3 确定接触载荷与阶跃力函数

滑板基座、支架、螺杆、螺母等材料为钢材，PU垫、轮为橡胶材料。由上所述，确定各接触副的参数，表1为ADAMS中部分材料的碰撞参数，代入各项参数。

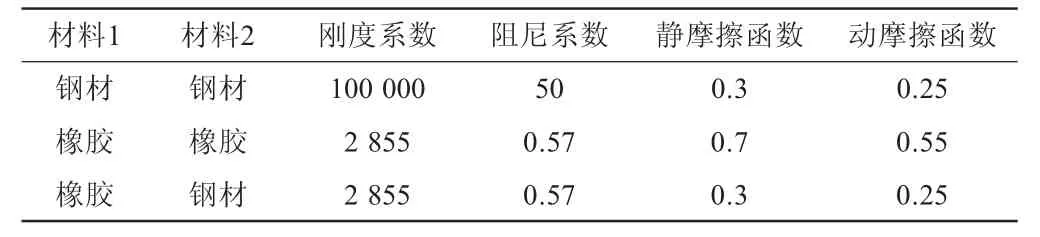
表1ADAMS部分材料碰撞参数

定义三个作用力，Force1水平作用于板面中心位置，提供滑板直行动力；Force2垂直作用于板面中心位置，模拟人给滑板的压力；Force3垂直作用于板面边缘，为滑板提供偏载。三个作用力STEP函数为：

Force1：STEP(time，0，20，0.5，0)

Force2：300*time

Force3：STEP(time，0.5，300，3，0)

2.4 仿真结果分析

经过仿真计算，得到板面倾斜角度γ随时间变化曲线图，如图6所示。由图可知，0.5 s前，滑板平稳向前运动，板面倾斜角度保持在0°，平行地面；0.5 s后，板面在受到偏载后发生倾斜，随时间变化倾斜角度趋于稳定，得到板面倾斜角度γ=90°-86.55°=3.45°。

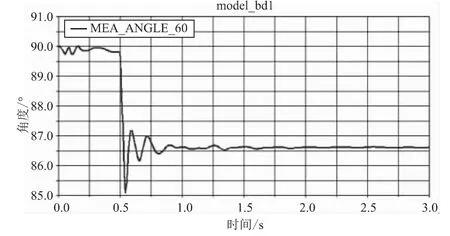
图6 板面倾斜角度γ随时间变化图

与此同时，得到了在板面倾斜状态下，前轴顺时针旋转角度δf，同时后轴逆时针旋转角度δr随时间变化曲线图，如图7、图8所示。由图可知，前轴与后轴都发生了相应的偏转，偏转角度为δf=2.9°，δr=3.7°。

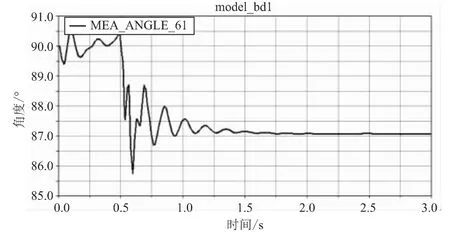
图7 前轴旋转角度δf随时间变化图

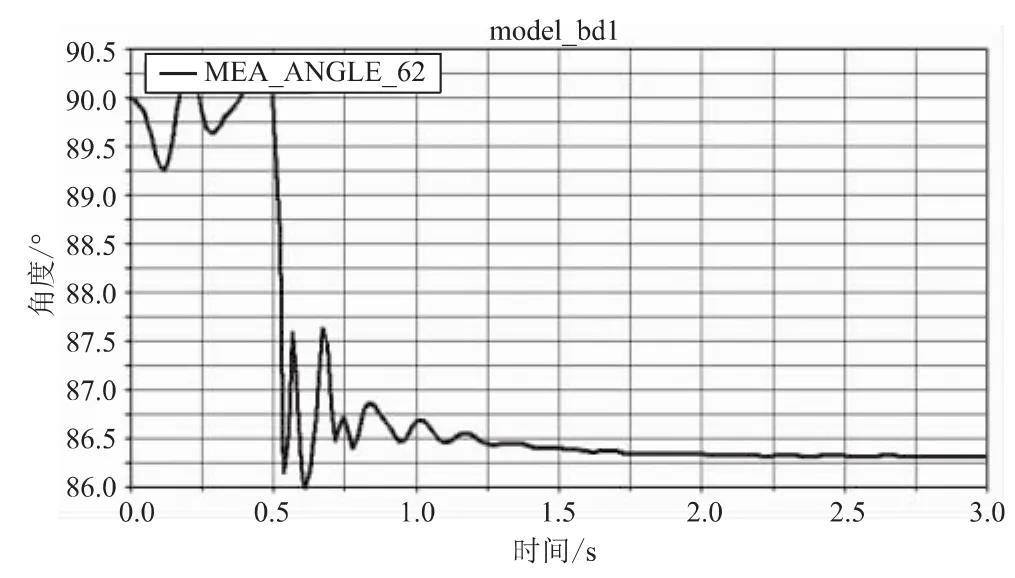
图8 后轴旋转角度δr随时间变化图

实测得λf=λr=42.3°，将λf、γ代入式（1）、（2）中，理论上可得δf=δr=3.14°，计算结果与仿真结果偏差不明显。从图中可以看出，滑板在0.5 s后，前后轴旋转角度都趋于一个稳定值，与实际情况相符。综上，验证了模型的可行性。

3 结论

本文从滑板的结构出发，采用微量旋转理论，得到滑板面倾斜角度与车轮旋转角度的函数关系，利用刚柔耦合建立多体动力学仿真，得到以下结论：

（1）根据矢量加法法则，得到前后轴旋转角度δf、δr与γ的数学关系。

（2）滑板前后轴旋转仿真结果与数学模型计算结果偏差不明显，且仿真过程中滑板前后轴旋转角度都趋于一个稳定值，与实际情况相符，验证了模型的可行性。

[1]胡小明，虞重干.体育休闲娱乐理论与实践[M].北京：高等教育出版社，2004.

[2]HUBBARD M.Skateboard-A Human Controlled Non-Holonomicsystem[J].Philosophical Transactions of The Royal Society,1979,46:931-936.

[3]HUBBARD M. Human control of the skateboard[J].Journal of Biomechanics,1980,13(9):745-754.

[4]KULESHOV A S.Nonlinear Analysis of the Skateboard Dynamics[J].Journal of Biomechanics,2007,40:400.[5]郑建荣.ADAMS——虚拟样机技术入门与提高[M].北京：机械工业出版社，2002.

[6]刘小平，郑建荣，朱治国，等.SolidWorks与ADAMS/View之间的图形数据交换研究[J].机械工程师，2003（12）：26-28.

[7]刘晓东，章晓明.基于ADAMS与NASTRAN的刚柔耦合体动力学分析方法[J].机械设计与制造，2008（2）：168-170.