多跳水声协作网络中的隐蔽通信与能量消耗优化
2018-02-06陈友淦刘均慧许肖梅
陈友淦,刘均慧,许肖梅
(厦门大学 海洋与地球学院,水声通信与海洋信息技术教育部重点实验室,福建厦门361102)
近年来,因具有可实现大面积覆盖、提高数据传输速率等优势,水声协作通信技术发展迅猛[1-3].与无线电磁波信道相比,水声信道具有载波频率低、带宽窄、波速低、多途延时长及多普勒频移相对较大等特点[1].Stojanovic[2]研究表明:通过短距离多跳实现中远程水声数据传输的水声协作通信系统,比直接进行远程水声通信更节约系统整体能量消耗;此外,由于传输距离的缩短,可适当提高工作频率、拓宽水声通信系统可用工作带宽,有利于提高水声通信速率.对于多跳水声协作通信网络,Kam等[3]从系统能量消耗优化角度研究了如何选择最优工作频率和布放节点位置的问题,同时指出:在由信源节点、中继节点、目的节点分布成一条直线的串行水声多跳系统中,当三者等距时,系统的整体能耗最小、性能最佳.然而,由于军事指挥、控制及通信、沿海监测和海底作战等特殊应用场景的需求发展,对多跳水声协作通信系统的隐蔽性要求越来越高[4].
目前,关于隐蔽水声通信的研究,主要集中在直序扩频水声通信的隐蔽性分析方面[5-6],较少涉及水声协作网络的隐蔽通信研究[4].相比之下,隐蔽射频通信和隐蔽雷达系统的研究则相对成熟,包括常规扩频、混沌电路和混沌调制,以及敏捷波形设计等[7-8].Weeks等[7-8]提出将低概率检测(low probability of detection,LPD)等作为点对点无线电磁波通信系统隐蔽性和隐身性的量化指标.LPD定义为在给定的恒虚警率条件下,“通用”能量检测器/截获接收机无法检测到检测概率高于0.5的通信信号,然而由于受到发射机特性、检测器参数、接收机行为和信道等多种因素的影响,LPD的测量值变化很大.Zheng等[4]研究表明,由于在水声协作网络中,通信接收机的高接收性能是通过中继节点形成空间分集增益获得的,而从隐蔽性角度看,截获接收机也将同样获得空间分集增益,故其LPD性能指标比点对点水声通信系统差.
因此,如何在维持水声协作通信系统高数据率、大覆盖范围、低系统能量消耗等优势的同时,兼顾满足隐蔽通信LPD指标,具有重要研究意义.本研究拟对多跳水声协作网络隐蔽通信的检测概率及系统能量消耗进行联合优化研究,通过分析不同目标信噪比、通信距离等因素对系统检测概率和能量消耗的影响,进行多跳水声协作网络的最优跳数选择分析.
1 系统模型与检测概率计算
1.1 多跳水声协作网络隐蔽通信系统模型
如图1所示,在所考虑的多跳水声协作网络隐蔽通信系统中,信源节点(Tx)、中继节点(Rk,k=0,1,2,…,K,当k=0时中继节点即为信源节点)和目的节点(Ds)分布在一条直线上,且K个Rk均匀分布在Tx和Ds之间,截获接收机(Ix)分布在Tx和Ds连线的中垂线上,其与该连线的距离为rmin.假设通过发送功率控制等措施,可让每个Rk只接收来自前一个Rk-1的信号并且向下一个Rk+1发送信号.
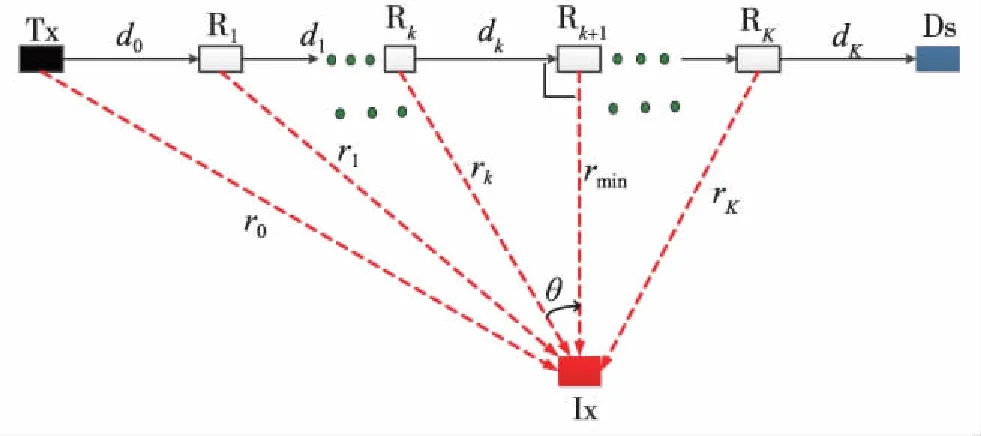
图1 多跳水声协作网络隐蔽通信系统模型(K取偶数为例) Fig.1Multi-hop underwater acoustic cooperative network covert communication system model (K is even as an example)
一般地,如图1所示,在每一跳中,检测距离比定义为截获接收机与发射机的距离和通信接收机与发射机的距离之间的比率[1],即
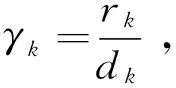
(1)
其中,rk为Ix到每个Rk的距离;dk为任意两个相邻Rk与Rk+1之间的距离.一般地,由于截获接收机必须靠近发射机才能截获到信号,所以检测距离比越小,通信系统的隐蔽性越好.由于Rk等距离分布,所以在图1所示模型中有
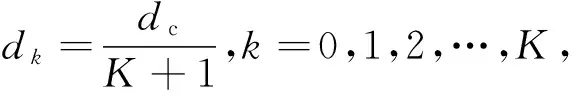
(2)
其中,dc表示Tx与Ds之间的距离,即通信距离.
1.2 多跳水声协作网络隐蔽通信系统检测概率的计算
为计算多跳水声协作通信系统的检测概率,首先计算点到点系统的检测概率.
假设Ds和Ix都经历相同带宽高斯噪声的水声信道,其具有等于N0/2的双边功率谱密度.若定义在Ix处能检测到的信号能量为Ei,Ds能正确接收数据所需要的信号能量为Es,点到点系统的检测距离比为γ,则根据发射信号能量与接收信号能量之间的关系,可得到
Ei=ηφEsγ-n.
(3)
其中:η表示Ds的通信接收机和通用宽带能量截获接收机之间的增益差异;φ表示接收信号中含检测兴趣目标的系数,与通信信号设计有关;n表示频带的路径损耗指数,与声波在水中的传播方式和传播路径有关.根据不同的传播条件,n取不同的数值.例如:当以球面波扩展传播时,n=2;而以柱面波扩展传播时,n=1;实际水声通信中,通常取n=1.5.
利用假设检验的方法[4-5],当时间带宽乘积很大时,虚警概率PFA和检测概率PD近似服从高斯分布,将式(3)代入相关计算公式[4-5],可求出点对点系统的检测概率为
PD=
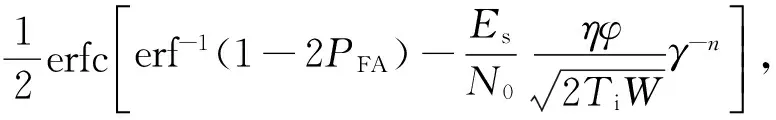
TiW≫1.
(4)
其中:Ti表示Ix的积分时间;W表示Ix的工作带宽,为3 dB带宽;erf和erfc分别表示误差函数和互补误差函数;Es/N0表示Ds能够正确接收信号时的信号能量噪声密度比.
对于K个Rk的通信系统,每一跳水声数据传输检测计算中rk均不等,Zheng等[4]提出了两种方法计算多跳系统整体的r:1) 取最小值,即r=min(rk);2) 取平均值,即r=E[rk],其中E[]表示对所有的rk取统计期望.本研究采用第2种方法计算r,即r=E[rk].因此,具有K个中继节点的系统检测距离比可表示为
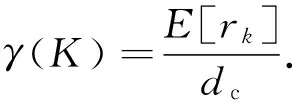
(5)
将式(5)带入式(4),可得到具有K个Rk的多跳水声协作通信系统的检测概率为
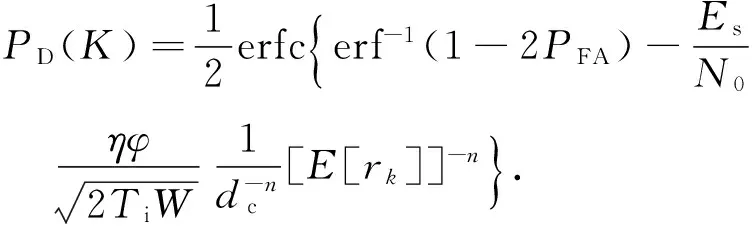
(6)
下面根据K的取值不同,通过图1的几何关系,具体计算E[rk].
假设Ix到Tx与Ds的最短距离为rmin,且任意rk等概率出现,当K为奇数时,有

(7)
当K为偶数时,有
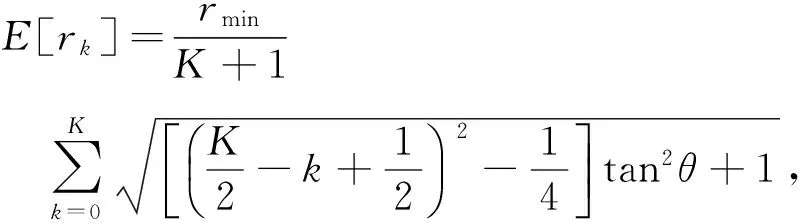
(8)
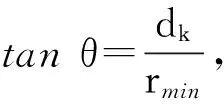
2 系统能量消耗的计算与跳数选择
2.1 多跳水声协作网络隐蔽通信系统能量消耗的计算
现考虑系统能量消耗问题,对于如图1所示的多跳水声协作网络隐蔽通信系统,其能量的衰减与通信距离和工作频率f有关,第k跳的传播损失为[9]
A(dk,f)=(dk)n[α(f)]dk,
(9)
其中,α(f)为吸收损失系数,其计算可由Thorp′s公式得到.将式(9)结合接收端的噪声功率密度谱N0(f),定义通信接收机接收端的平均信噪比为
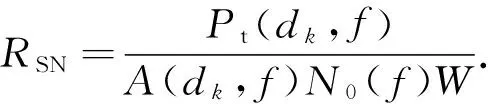
(10)
其中:Pt表示Tx的发射声源级所对应的数值;N0(f)的计算可参考Wenz噪声;W表示通信接收机的工作带宽,由于本研究假设其与Ix的工作带宽相等,故用同一符号表示.在给定距离的情况下,选择最优工作频率,可使A(dk,f)N0(f)乘积最小,进而实现在相同平均信噪比情况下系统能量消耗最少的目标[3].在每一跳中,最优工作频率fopt(dk)与工作距离dk有关,此时所对应的工作带宽为3 dB带宽,具体计算可参考文献[3]给出的拟合公式.
若只考虑Tx、Rk、Ds解码和编码的能量,以及发射和接收信号所需要的能量,暂时忽略重传和误码率的影响,即假设每一跳只需传输一次则通信接收机即可正确接收信号,同时假设每个Rk或者Ds接收信号所需要的能量相同,则对于每一跳而言,发射机的能量消耗为
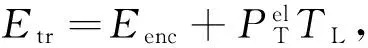
(11)
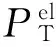
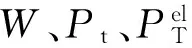
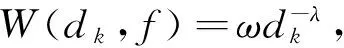
(12)
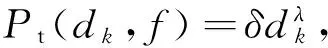
(13)
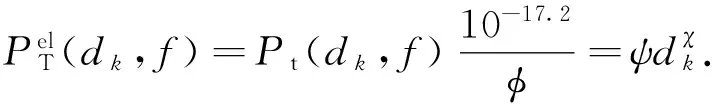
(14)
其中:10-17.2是转化因子[9]数值,其单位为W,可将发射声源级所对应的数值转换为单位为W的电功率;φ是整体功率放大器和换能器的效率;ω、δ和ψ表示相应的扩展系数,ψ的取值与目标信噪比RSN0有关,λ和χ表示相应的指数,其取值均为正值,可在对数尺度上通过一阶最小二乘多项式逼近计算得到.
同样,对于每一跳而言,接收机的能量消耗为
Err=Edec+PRTL.
(15)
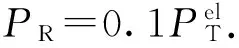
因此,对于一个有K个Rk的水声多跳协作通信网络传输信号消耗的系统总能量为
Esys(K)=(K+1)Etr+(K+1)Err.
(16)
2.2 跳数优化选择
在上述基础上,在兼顾检测概率满足LPD要求的多跳水声协作网络隐蔽通信系统中,以最小化系统总能量消耗为目标函数的跳数K优化选择,可表达为
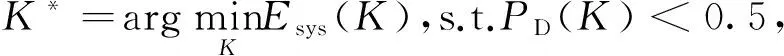
(17)
式中,K*表示待求的最优跳数.
下面对跳数K的优化选择进行理论推导.
1) 从能量优化角度看
(K+1)(Edec+PRTL)=(K+1)
(18)
其中,ρ表示编解码消耗功率与发射信号消耗功率之间的差别系数,σ表示接收机消耗功率与发射机消耗功率之间的差别系数.将式(2)和(14)代入式(18)有
Esys(K)=(K+1)(σ+2ρ+1)ψdkχ
(K+1)1-χ=Ω(K+1)1-χ,
(19)
对K求导,有

(20)
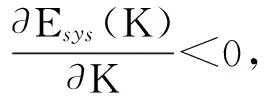
若给定系统的目标能量消耗Esys(K)<ε0,代入式(19)可得
Ω(K+1)1-χ<ε0,
(21)
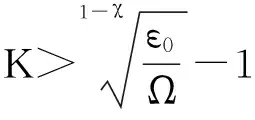
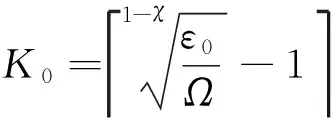
2) 从满足检测概率角度看
由式(6)可知
(22)
其中,β与PFA有关,ξ与信噪比、通信接收机和截获接收机之间的增益差异、通信信号设计等有关.
给定检测概率门限PD0(若按照LPD要求,则PD0=0.5),则有
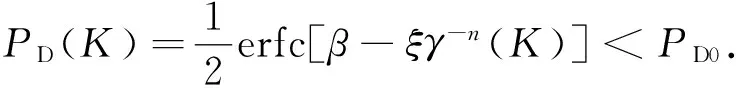
(23)
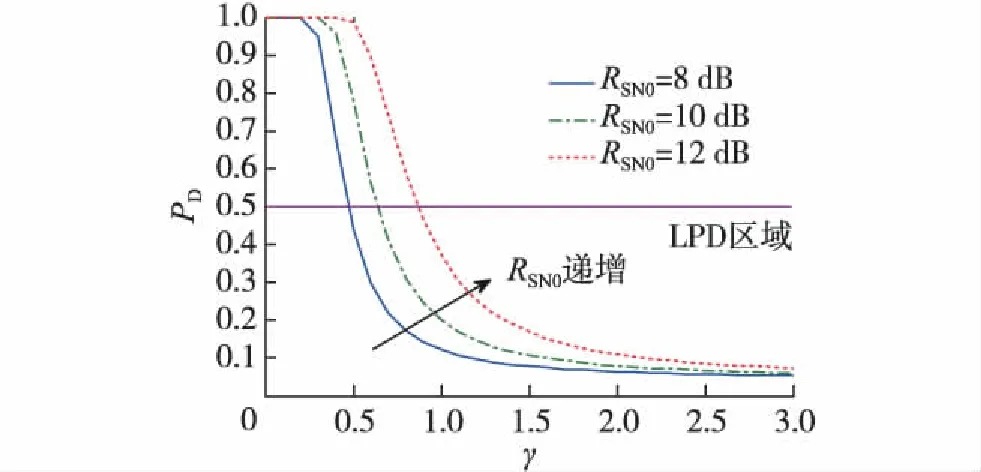
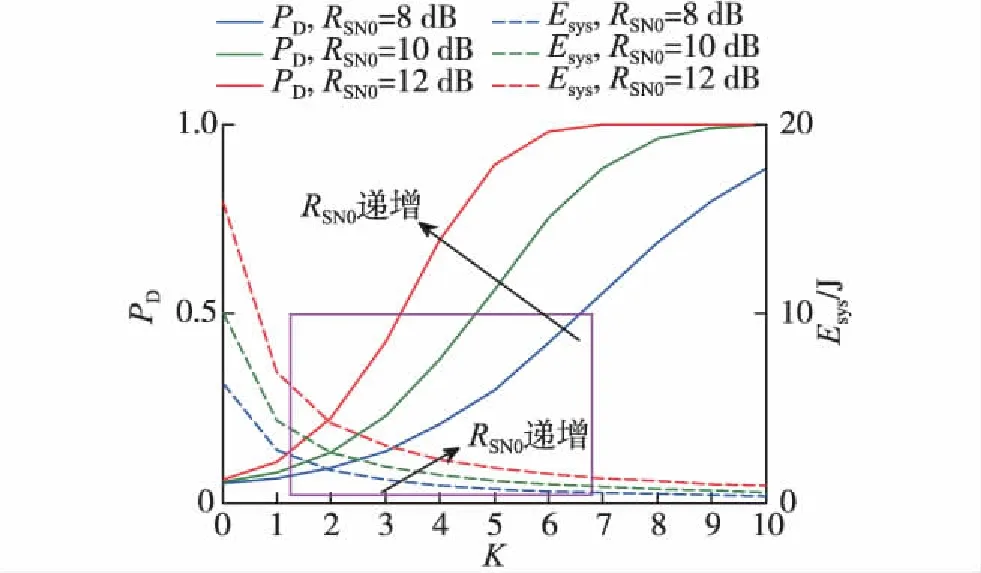
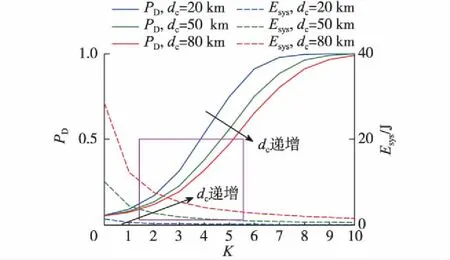
通过式(23)直接求解K难度较大,可通过计算机仿真求数值解.通过后续计算机仿真可知,在给定条件下,PD(K)随着K递增呈递增关系,则可假设式(23)解为K 3) 综合讨论分析 综上,跳数K的取值范围为K0≤K≤K1,其中K0和K1的取值与系统参数设置、目标检测概率、目标能量消耗率等有关.由上述分析可知,PD(K)和Esys(K)是两条趋势相反的曲线,一旦系统参数设置、目标信噪比给定,则曲线PD(K)和Esys(K)也随之固定,可根据目标检测概率、目标能量消耗率求出满足条件的K的取值范围;在取值范围内,K的具体取值范围由功耗和检测概率的侧重需求决定. 取通信距离为50 km,图2给出了点对点水声通信系统不同RSN0条件下检测概率与检测距离比之间的关系(图中PD<0.5的区域即为LPD区域).可见,在相同PD条件下,RSN0越低,所需的检测距离比越低,意味着截获接收机需要越靠近发射机才能达到同样的检测概率,说明通信系统隐蔽性更好.在通信距离为50 km时,以PD=0.5为目标,若RSN0从12 dB降低到8 dB,则Pt也从166.442 5 dB降低到162.442 5 dB(可由式(13)和(14)计算得到),γ可从0.875降低到0.500.因此,设计良好的通信信号,降低通信接收机正确解码所需的RSN0,是进行低功耗水声隐蔽通信的关键. 图2 点对点水声通信系统不同RSN0条件下 检测概率与检测距离比之间的关系 Fig.2The relationship between probability of detection and distance ratio with different RSN0 for point-to-point underwater acoustic communication system 3.2.1 不同RSN0的影响 为进一步了解不同RSN0在多跳水声协作通信系统下的情况,图3给出了不同RSN0条件下PD、Esys与K之间的关系.由图3可知,无论RSN0取值如何,随着跳数K递增,多跳水声协作通信系统的Esys递减,而PD却是递增的,趋势正好相反;为维持相同的PD,随着RSN0递增,跳数K必须减少,因为RSN0递增增大了瞬时功率,更容易被截获.例如,为维持PD=0.42不变,当RSN0从8 dB递增到12 dB时,跳数K必须从6减少到3,否则容易被截获. 图3 不同RSN0条件下检测概率、 能量消耗与跳数之间的关系 Fig.3The relationship between probability of detection,energy consumption and number of hops with different RSN0 综合判断,在给定的基本仿真条件下,在图3的矩形方框内(即LPD区域内),RSN0取8 dB时,K取2~6,可满足PD<0.5的LPD要求,同时Esys也相对较低;若RSN0取12 dB,则跳数K只能取2~3,方可兼顾LPD性能指标和系统低功耗要求. 3.2.2 不同dc的影响 图4 不同传输距离条件下检测概率、 能量消耗与跳数之间的关系 Fig.4The relationship between the probability of detection,the energy consumption and the number of hops with different transmission distance 图4给出了不同dc对PD和系统Esys的影响.由图4可见,随着dc的递增,系统的Esys是递增的;与此同时,当dc为20 km时,跳数K取3,PD=0.315 3,Esys为0.249 7 J;而当dc为80 km时,K也取3,则PD可降低到0.195 0,Esys为5.325 8 J.可见,在K相同且其他条件均不变的情况下,随着dc的递增,dk也在递增,相当于降低了多跳带来的容易被截获的风险,进而降低了总体的PD.另一方面,当dc为80 km时,K增加到4,PD仅为0.318 0,Esys降低到4.067 9 J,即使跳数K增加到5,PD也仅为0.474 0,仍未超过PD<0.5的LPD要求,同时Esys降低到3.264 1 J;而当dc为80 km时,跳数K从3增加到5,Esys可从5.324 8 J降低到3.264 1 J,降幅高达38.7%,同时满足LPD要求.可见,在相同PD的情况下,随着dc递增,K可适当增加,这有利于降低系统整体的能量消耗. 综合判断,在给定的基本仿真条件下,多跳水声协作通信系统的dc为80 km时,K取2~5,可满足PD<0.5的LPD要求,且Esys也相对较低;若dc取20 km,则K只能取2~3,方可兼顾LPD性能指标和系统低功耗要求. 为维持多跳水声协作网络宽带宽、高数据率和低功耗的优势,同时满足隐蔽通信的性能指标,研究了多跳水声协作通信系统中的跳数优化选择问题.通过建立多跳水声协作网络隐蔽通信系统模型,建立了其检测概率和能量消耗计算模型,推导了联合检测概率、能量消耗优化与最佳跳数选择的取值范围,最后通过仿真研究分析了不同目标信噪比、通信距离等因素对系统检测概率、能量消耗和最佳跳数选择的影响.仿真结果表明,为维持相同检测概率,随着目标信噪比递增,跳数必须减少,以防止由于瞬时功率过大而被截获;在相同检测概率情况下,随着通信距离递增,跳数可适当增加,有利于降低系统整体的能量消耗;在总通信距离50 km,数据长度256 byte,RSN0为10 dB,截获接收机的位置参数角度为π/15时,跳数取值在2~6之间,可满足检测概率小于0.5的隐蔽通信要求,同时能量消耗相对较低. [1] VAJAPEYAM M,VEDANTAM S,MITRA U,et al.Distributed space-time cooperative schemes for underwater acoustic communications[J].IEEE J Ocean Eng,2008,33(4):489-501. [2] STOJANOVIC M.Capacity of a relay acoustic link[C]∥IEEE Proc of MTS/IEEE OCEANS 2007.Canada:IEEE,2007:1-7. [3] KAM C,KOMPELLA S,NGUYEN G D,et al.Frequency selection and relay placement for energy efficiency in underwater acoustic networks[J].IEEE J Ocean Eng,2014,39(2):331-342. [4] ZHENG Y R,FAN L L.Performance metrics for mow probability of detection in cooperative communication networks [C]∥IEEE Proc of IEEE/MTS OCEANS 2016.Shanghai:IEEE,2016:1-5. [5] YANG T C,YANG W B.Low probability of detection underwater acoustic communications using direct-sequence spread spectrum [J].J Acoust Soc Am,2008,124(6):3632-3646. [6] 柳文明,韩树平,李厚全,等.基于截获因子的直序扩频水声通信隐蔽性能分析[J].南京大学学报(自然科学版),2017,53(4):654-660. [7] WEEKS G,TOWNSEND J,FREEBERSYER J.A method and metric for quantitatively defining low probability of detection[C]∥IEEE Proc of IEEE Military Communications Conference.Piscataway:IEEE,1998:821-826. [8] DILLARD G M,DILLARD R.A metric for defining low probability of detection based on gain differences[C]∥IEEE Proc of IEEE Military Communi Cations Conference.Piscataway:IEEE,2001:1098-1102. [9] SOUZA F A D,CHANG B S,BRANTE G,et al.Optimizing the number of hops and retransmissions for energy efficient multi-hop underwater acoustic communications[J].IEEE Journal of Sensors,2016,16(10):3927-3938. [10] STOJANOVIC M.On the relationship between capacity and distance in an underwater acoustic communication channel[J].ACM SIGMOBILE Mobile Comp Commun Rev,2007,11(4):34-43.3 仿真分析
3.1 仿真条件
3.2 仿真结果与讨论
4 结 论
