基于可视化技术的曲面加工误差分析及应用*

邵 伟 彭 鹏 王 错 周阿维

(① 西安理工大学, 陕西 西安 710048；② 西安工程大学, 陕西 西安 710048)

精密测量技术是推动国民经济发展的重要基础技术之一，是先进制造中不可或缺的重要组成部分。随着我国现代工业的发展，尤其是以数字制造为核心的先进制造技术的迅猛发展，对精密测量技术提出了新的要求：一方面要为先进制造技术担负起质量技术保证的重任；另一方面又不能单纯为检测而检测，还要为产品生产效益的提高贡献力量[1-2]。随着国民经济的迅猛发展，诸如汽车制造、船舶制造、航空航天、水利水电、武器装备等领域对大尺寸测量技术提出了越来越高的期望和要求[3-4]，尤其是对于重型、易变形的曲面工件检测提出了越来越高的要求。因此，亟待研究曲面检测新技术和检测系统，以满足目前市场的需求，保证机床的利用率及产品加工质量。

而检测数据处理完成后，进行检测结果的应用对在线检测具有重要的意义。曲面检测的目的是判断所加工的曲面是否能满足要求，主要是模型精度评定，即了解由测量数据所重构的曲面模型和理论模型之间的误差分布情况。对曲面工件进行评估后，可以检查曲面工件的加工质量，此外也可利用获得的几何尺寸信息对曲面工件生产工艺进行改进，使工件的废品率降低，从而提高经济效益[5]。

曲面不像一般规则的几何元素那样，能用有限参数给出精确定义，对其加工精度的检验变得较为复杂。并且难以用精确的数学模型定量描述工件成形效果和加工工艺参数之间的关系。工业生产中，主要采用基于经验数据和反复试验渐进的方法确定合适的加工成形工艺参数，成本高、周期长。因此，本文采用建立可视化的检测误差模型及表示方法并利用基于神经网络技术的专家系统获得后续加工所需工艺参数，指导后续的数控加工，提高系统加工质量和加工效率。

1 曲面检测误差可视化模型的建立

精度有较高要求的应用中，检测误差分析常常是非常重要的。因此，针对曲面工件的加工精度，本文采用了基于检测误差模型(inspection error model，IEM)的误差评估方法，即首先对工件进行测量后，由测量数据进一步得到重构模型，将重构模型与CAD模型进行配准，保证测量坐标系与设计坐标系一致，然后通过CAD模型上的测点和数控机床返回的检测结果进行单点比较的方法进行单点的误差计算，最终获取模型间的检测误差信息，从而建立起检测误差模型，以便进行分析评估。

建立检测误差模型之前，首先要保证测量坐标系与设计坐标系一致，将理想模型(CAD模型)上的测点Ps(xs,ys,zs)与机床上返回的该点实测的位置Pm(xm,ym,zm)按式(1)进行计算，得出该点在法矢方向的距离定为当前的误差值，正值表示该点的加工余量，而负值则表示该点过切。

(1)

本文建立的IEM是为了进行精度评价和误差分析，并把它定义为：由曲面片集以及曲面误差信息组成的模型。它完整地记录了产品的几何信息和检测误差信息(参见表1)。IEM是以配准后模型与CAD模型间的偏差为基础建立起来的，其思想同样可以应用于逆向工程中的制造精度分析，重构精度分析以及仿制精度分析。制造精度分析是指基于以CAD模型进行制造件加工精度的检测，重构精度分析是指以原型件为参考检测重构模型的过程，仿制精度分析是指原型件和复制件之间的定量比较。

表1 检测误差模型的内涵

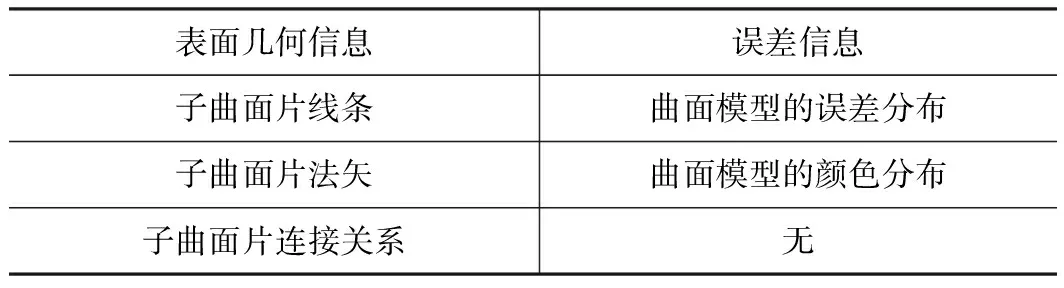
表面几何信息误差信息子曲面片线条曲面模型的误差分布子曲面片法矢曲面模型的颜色分布子曲面片连接关系无

1.1 曲面检测误差可视化映射关系建立

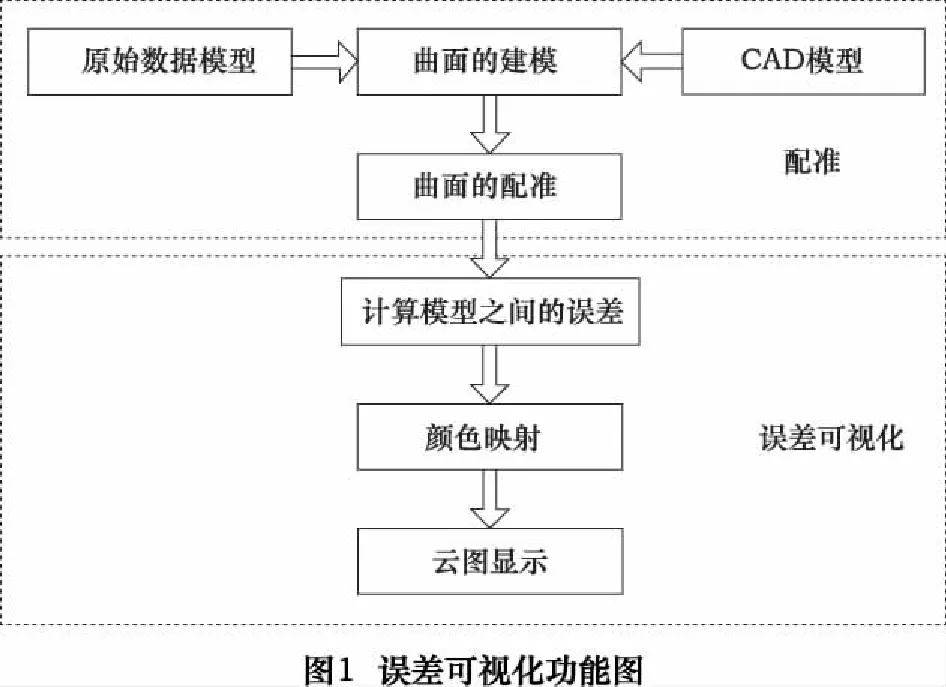
为了将曲面误差结果直观形象地反馈给用户，通常将IEM结合数据可视化技术，建立了误差与灰度值之间的映射关系，从而利用彩色云图来表示重构模型的误差分布，为分析人员提供了一种可视化的分析手段。IEM的可视化包括以下几个主要步骤：第一步是误差数据生成；第二步是可视化映射，将误差数据转换为可供绘制的几何图素和属性；第三步是将产生的几何图素和属性转换为可供显示的图像。IEM的可视化功能图如图1所示。下面先对颜色灰度值映射模型进行介绍。

1.1.1 RGB灰度值模型及其插值算法

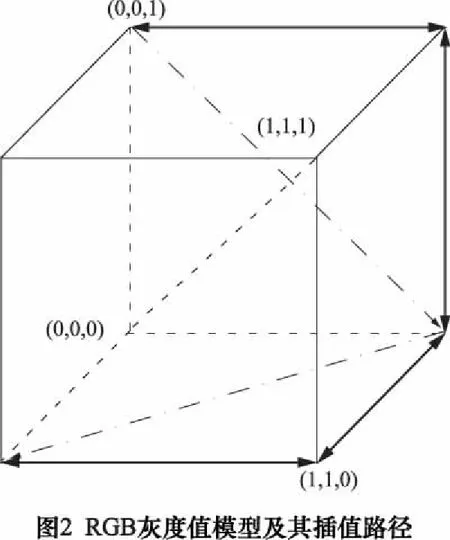
对应不同的应用场合有多种不同的RGB灰度值描述方法或称RGB灰度值模型[6-7]，其中RGB灰度值模型通常用于图形显示器上，它采用直角坐标系，通常由R(红)、G(绿)、B(蓝)坐标轴定义的单位立方体来描述，如图2所示。在正方体的主对角线上，各原色的量相等，产生由灰度值(0,0,0)到灰度值(1,1,1)的灰度变化。正方体的其他6个角点分别为(1,0,0)、(1,1,0)、(0,1,0)、(0,1,1)、(0,0,1)和(1,0,1)。

为了设计出无数种灰度值，使得给定变量x值和灰度值空间的某一子集一一对应，可以采用灰度值插值的策略实现。在实际中，简单的灰度值插值算法是三色线性灰度值插值，首先分别指定两极值点和中值点的灰度值：RGBmin、RGBmax、RGBmd，其他的灰度值可通过式(2)的线性插值函数计算得到。

(2)

其中xmin、xmax分别为给定变量x的最小值、最大值。如插值路径如图2单点划线所示，其插值函数为：

(3)

由于三色线性灰度值插值算法用到的灰度值较少，色彩比较单调。为得到对比鲜明，变化丰富的视觉效果，可采用更多色的插值策略。在此本文采用了一种五色线性灰度值插值算法，插值路径如图2中粗双箭头线条所示，则插值函数为：

(4)

1.2 曲面检测误差可视化实现过程

为了直观地表示配准后模型与CAD模型间的误差分布，首先将配准后模型中的重复点去掉；然后求取配准后模型到CAD模型间的误差；再将误差值同RGB灰度值映射起来；最后将模型的误差分布用可视化的形式表示出来。其中主要技术是利用RGB灰度值技术将检测误差的数值点用对应的RGB灰度值表示，对照RGB灰度值，研究人员就可以通过RGB灰度值视图形象地看到检测误差分布情况。该RGB灰度值能从检测误差参数数据中自动查找出检测误差参数绝对值的最大值Ermax，并根据差值(Ermax-0)等分出若干检测误差区域，即进行颜色标号，然后遵循人们的习惯或用户要求的对应关系来实现检测误差与RGB灰度值的映射，并且令误差为零处显示为RGB(0,0,255)，最大误差处显示为RGB(255,0,0)，对于位于零与最大偏差之间的偏差，在其之间进行线性插值。把连续变化的检测误差人为地映射成阶梯跳跃的RGB灰度值，计算出曲面检测误差值所对应的RGB灰度值。这样任意一个误差与RGB灰度值映射表对应起来，再将这个RGB灰度值映射到相应的数据点，形成了误差可视化云图。

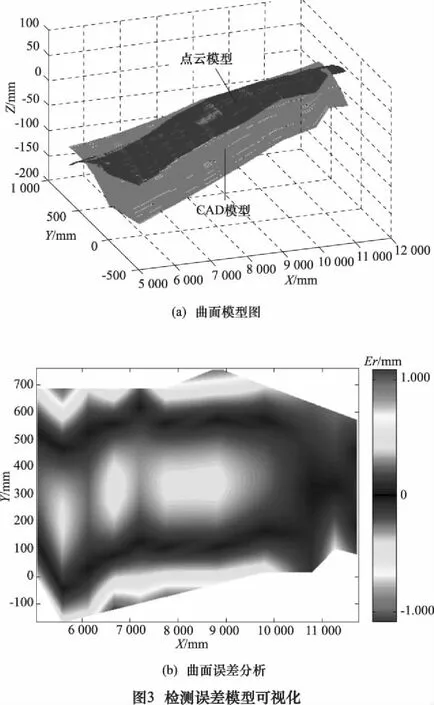
1.3 曲面检测误差可视化实现结果

以某曲面为例，将配准后模型与CAD模型间的误差分布用可视化云图表示如图3所示。图3a为测量点云模型及其CAD模型，图3b为误差分布结果。

2 基于曲面检测误差模型的工艺参数改进

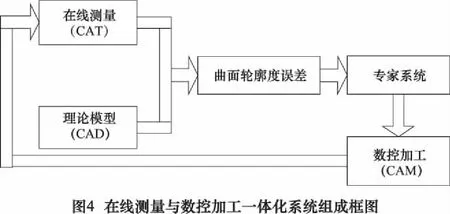
如图4所示为大型曲面在线测量与数控加工一体化系统，即在曲面数控加工之后，进行在线测量，将测量结果与CAD模型数据进行比对，得到曲面检测误差模型，然后通过专家系统获得数控加工所需工艺参数，指导数控加工的进行。该系统的一个重要的环节就是专家系统。

由于传统专家系统只能处理显性的表面的知识，推理能力弱，智能水平低等，而神经网络能高度逼近非线性系统并对复杂不确定系统具有自适应和自学习能力[8]，因此采用具有多层前馈式误差反向传播(error back-propagation, BP)神经网络模型来进行大部分的知识获取，其获取的知识存储在网络的权值和阈值当中，并由网络的并行计算而得到网络的输出结果。然后，将网络输出结果转换成专家系统推理机能接受的形式，由专家系统的推理机得到数控加工的工艺参数。

2.1 神经网络专家系统的构成

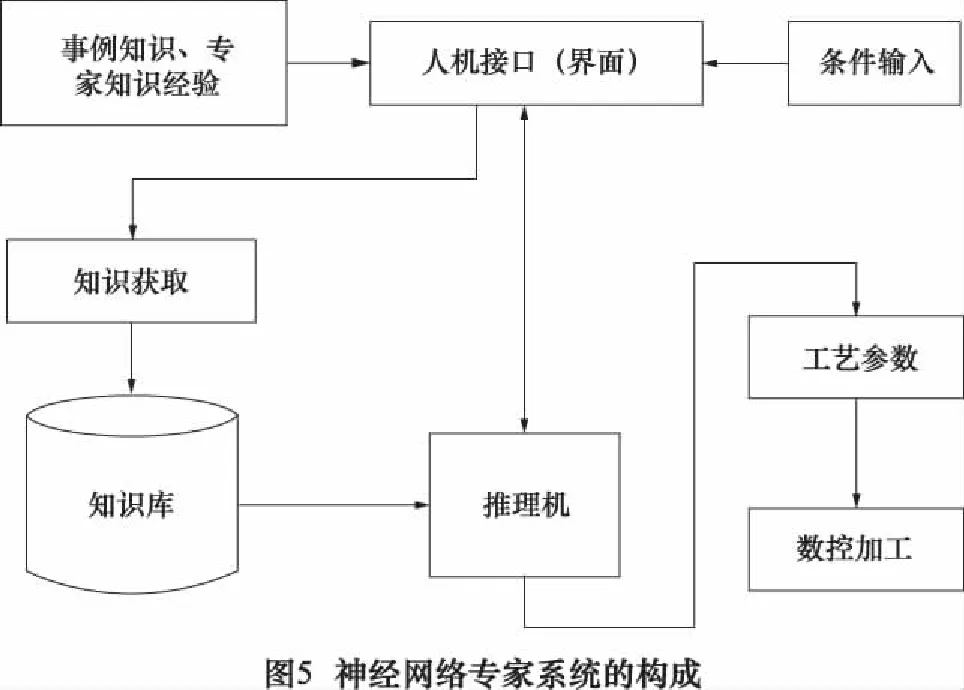
如图5所示，该神经网络专家系统主要由人机接口、知识获取模块、知识库、推理机等部分组成[9-10]。知识库是专家系统的核心。如果输入曲面工件的几何信息、厚度、物性参数等，系统根据知识库中的实验数据库、专家知识、已建立的数学模型和算法等方法进行推理、判断，就能得到合理的工艺参数。

2.2 知识获取

专家系统的核心是知识，因而在一个专家系统建造中，解决知识如何获取是一个十分重要的课题[11]。在专家系统开发过程中，知识获取是最难解决的一道工序，被认为是专家系统建造中的“瓶颈”问题。只有当知识获取的手段自动化、智能化后，才可以说专家系统有了真正的智能。

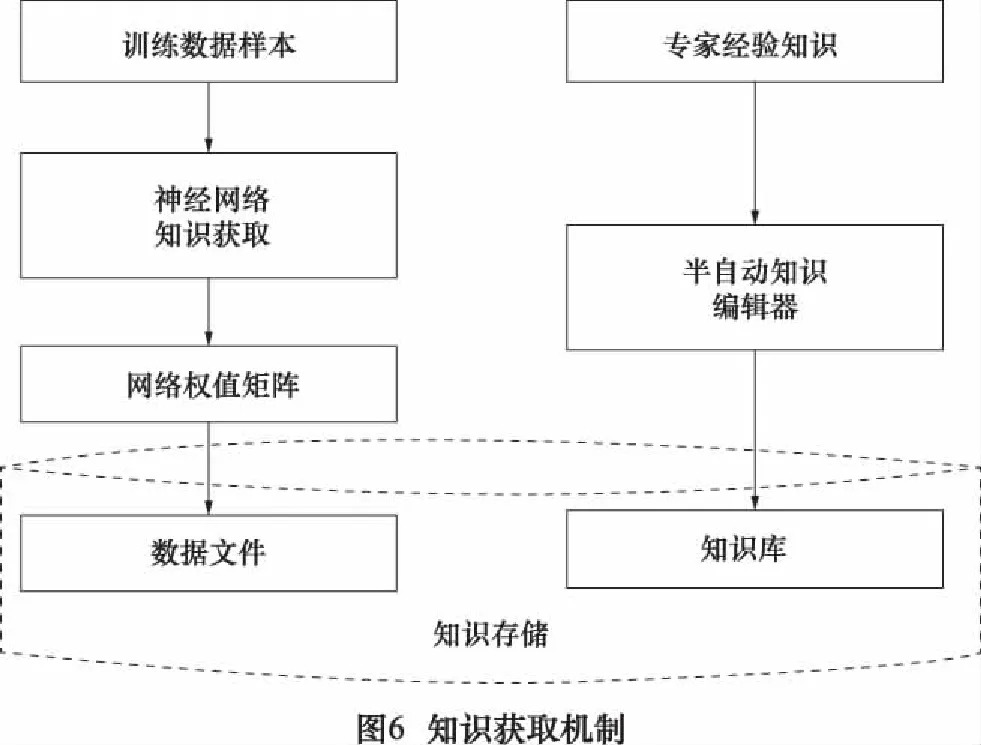
本文涉及到两部分知识的获取：一是传统描述性知识获取；二是从实例样本中获取隐含性知识。第一部分采用半自动化的知识获取工具，领域专家可以根据界面向导，不需要知识工程师帮助，方便地将领域知识及经验录入到知识库中；第二部分用人工神经网络进行知识的自动获取。通过神经网络对样本数据的学习，将其中隐含的知识存储到整个网络中，并用数据文件的形式保存网络的权值和阈值。此种知识获取机制的结构如图6所示。

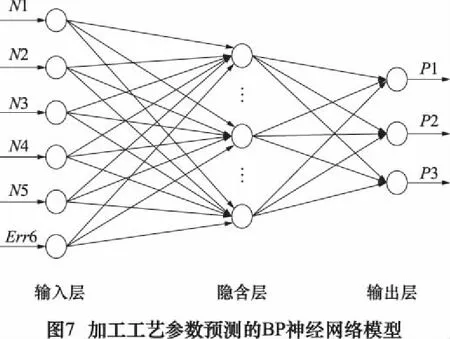
大部分的知识获取可采用BP网络模型来进行，BP网络由输入层、输出层和若干隐含层构成，每层由若干个结点组成，每一个结点表示一个神经元，上层结点与下层结点之间通过权连接，同一层结点之间没有联系。由于BP神经网络具有逼近任意连续函数和非线性映射的能力，因此在神经网络研究领域中得到了广泛的应用，其结构简单，可操作性强，能模拟任意的非线性输入输出关系。利用BP网络获取知识的基本思想是：首先提供足够数量的学习样本供网络训练，通过调整网络权值使得输入信息通过输入层经隐含层逐层处理并计算出的网络输出尽可能的接近期望输出，通过训练，将网络的权值调整到合适的值，使得对所有样本都能够得到期望输出，这时，网络的训练就结束了，就可以用该网络来进行知识的自动获取了。BP网络训练采用的学习样本由输入和期望输出两部分数据组成，如图7所示。网络的输入是曲面工件的物性参数中的弹性模量N1、泊松比N2、屈服强度N3和硬化指数N4，以及工件厚度N5、工件曲面的检测误差值Err6。该网络的期望输出是对应的数控加工工艺参数，以喷丸成型加工为例，其工艺参数为弹丸流量P1、喷射气压值P2和机床速度P3。

2.3 推理机制

推理机实质上是计算机的一组程序，目的是用于控制、协调整个专家系统的工作。它根据当前的输入数据或信息，再利用知识库中的知识，按一定的推理策略去处理、解决当前的问题。

在该系统中，采用的推理策略为正向推理，系统根据输入的数据，在知识库中找到神经网络的权值矩阵的有关数据。然后，计算神经网络的输出，根据此输出进行数控加工工艺参数调整的指导，最后给出推理结果。具体推理步骤如下：

(1)将输入数据加到神经网络输入层的各个神经元。

(2)按照已确定的网络传递特性和输入数据计算输入层各神经元的输出，并把它们作为隐含层单元的输入。

(3)再分别计算隐含层神经元及输出层神经元的输出。

运用神经网络算法，可以精确地计算出数控加工的工艺参数值，从而为进一步的加工提供了依据。

3 实验分析

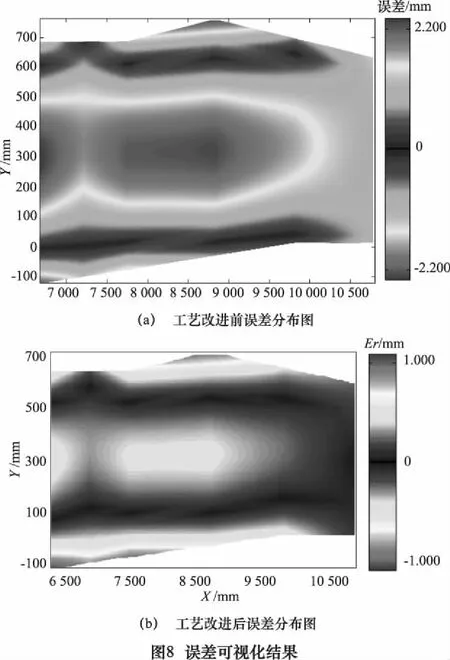
以某曲面壁板零件加工为例，对壁板曲面进行检测的误差结果如图8a所示；然后，通过专家系统获得加工所需工艺参数，指导加工，可得到修改后的曲面检测的误差结果如图8b所示。由图8可知，根据曲面在线检测误差对数控加工工艺参数进行改进，再加工得到的曲面与理论模型的误差明显减小，这样使工件的废品率降低，从而提高生产效率和经济效益。

4 结语

本文对曲面检测误差模型的建立和表示方法进行了研究，首先建立了检测误差模型，实现了检测误差的数字化传递，然后用可视化云图对误差结果进行直观的表示，并对误差结果进行分析，最后通过基于BP人工神经网络的专家系统获得数控加工所需工艺参数值，从而为进一步的数控加工提供了指导依据，有效地提高了加工精度和加工效率。

[1]裘祖荣，石照耀，李岩.机械制造领域测量技术的发展研究[J].机械工程学报，2010，46(14)：1-11.

[2]陈巧巧.浅谈数控机床在线测量技术[J].计量与测试技术, 2012, 39(6):37-39.

[3]Savio E, Chiffre LD,Schmitt R.Metrology of freeform shaped parts[J].CIRP Annals.Manufacturing Technology,2007, 56(2):810-835.

[4]郑联语, 朱绪胜, 姜丽萍.大尺寸测量技术在航空制造业中的应用及关键技术[J].航空制造技术, 2013, 427(7):36-41.

[5]孙郅佶，安晨辉，杨旭，等.超精密机床主轴回转误差在线测试与评价技术[J].制造技术与机床, 2015(9):118-123.

[6]项志钢.计算机图形学[M].北京：清华大学出版社，2008.

[7]陈敏雅, 金旭东.浅谈计算机图形学与图形图像处理技术[J].长春理工大学学报, 2011(1):142-143,150.

[8]Joseph C Giarratano, Gary D Riley. 专家系统:原理与编程:principles and programming [M].北京：机械工业出版社，2006.

[9]别秀德.BP神经网络应用研究[J].智慧工厂, 2016(1):97-102.

[10]Bangalore P, Tjernberg L B.An artificial neural network approach for early fault detection of gearbox bearings[J].IEEE Transactions on Smart Grid, 2017, 6(2):980-987.

[11]冯定.神经网络专家系统[M].北京：科学出版社，2006.