富春江电站与之江水文站径流量相关关系研究

李若华，黄士稳

（1.浙江省水利河口研究院，浙江 杭州 310020；2.浙江省河口海岸重点实验室，浙江 杭州 310020；3.浙江省水文局，浙江 杭州 310009）

1 问题的提出

潮流量是河口开发、整治与河口科学研究的一项基本资料[1]。钱塘江富春江电站以下为感潮河段，称为钱塘江河口（见图1）。富春江电站于1968年12月建成使用（控制流域面积为31 829 km2），河口干流径流量以富春江电站下泄流量为准，至今已有近50 a的资料。富春江电站至闻家堰河段长75 km，水动力以径流作用为主，称为河流段，沿线有分水江、渌渚江、壶源江、浦阳江等9条一级支流汇入；闻家堰以下河段受径流、潮汐共同作用，称为过渡段[2]，因江道宽，潮量大，水流形势复杂，潮流量观测难度极大。闻家堰河段江道较窄，2008年在该河段设立了之江水文站（控制流域面积为41 769 km2），尝试采用声学多普勒测流技术对之江断面的潮流量进行高频次观测（时间间隔5 min），并不断改进推求方法，推算经过该断面的净下泄流量[1]。

富春江电站有近50 a的径流量资料，而之江水文站仅有不足10 a的资料，若两者能够建立相关关系，则可以大大延长之江水文站的径流量资料，这对分析钱塘江入海径流量等相关研究具有重要意义。因此，本文力求通过回归分析的方法研究富春江电站与之江水文站径流量的相关关系，并对推求结果进行误差分析。成果可供相关研究人员参考和采用。

2 资料及研究方法

2.1 水文资料

为掌握钱塘江年入海径流量，浙江省水文局2008年在钱塘江之江断面左、右岸各设置了1台声学多普勒流速仪，将 2 台定点式声学多普勒流速仪所测到的流量作为一个整体，通过实测资料分析，找出整体的平均流速与断面平均流速的关系，使用手工定出的曲线推流得到之江水文站的潮流量，对潮流量进行时间上的积分即可得到某一时间段的净泄流量[1]。

之江水文站经过2 a试运行，2010年以后的径流量数据基本合理，故资料采用2012年（代表丰水年）、2014年（代表平水年）之江水文站及富春江电站的逐日平均径流量数据进行相关分析，因2010年以后均为丰水、平水年，尚缺少枯水年的资料。

2.2 研究工具

采用美国Origin Lab公司开发的Origin软件对日平均流量、旬平均流量、月平均流量进行回归分析，以研究不同时间尺度下流量的相关性。在回归分析时采用了线性拟合和多项式拟合2种方法，对比发现2种结果的拟合公式和精度差异很小，为简便起见，采用线性拟合研究之江水文站与富春江电站径流量的相关性。

3 结果分析

3.1 月平均流量回归分析

采用月平均流量资料对之江水文站与富春江电站的径流量进行回归分析，结果见图2 ～ 4。由图2 ～ 4可知，2站月平均流量的相关性较强，数据点基本上都集中在趋势线的附近，2014年相关系数可以达到0.9970，2012年相关系数也可达到0.9896，汇总2 a资料回归的相关系数介于两者之间，为0.9904。

采用不同拟合公式推算之江站月平均流量的误差分析见表1，公式1（以下同2012年）的计算结果大于公式2（2014年），公式3的计算结果介于公式1、公式2之间，与公式1、公式2计算结果的平均值接近，且流量越大，公式3的计算结果越接近于公式1的计算结果；另外还可得出，流量越大，采用公式3计算与公式1、公式2计算结果的相对误差越小，当流量大于1 000 m3/s时，误差基本小于5%。

总体来说，2站月平均流量的相关性较好，基于回归公式由富春江电站的月平均径流量可以推算之江水文站的月平均径流量，因公式3汇总了2 a的资料，计算结果介于公式1、公式2之间，代表性更强，误差更小，建议作为推算之江水文站月平均径流量的计算公式。

图2 2012年月平均流量回归分析图（公式1）

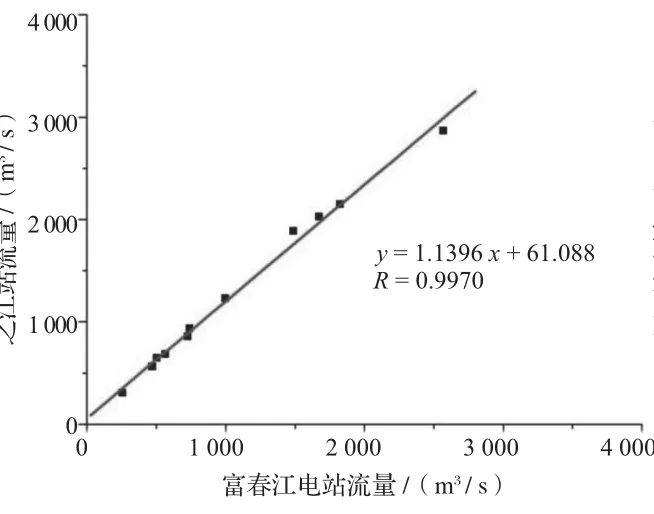
图3 2014年月平均流量回归分析图（公式2）

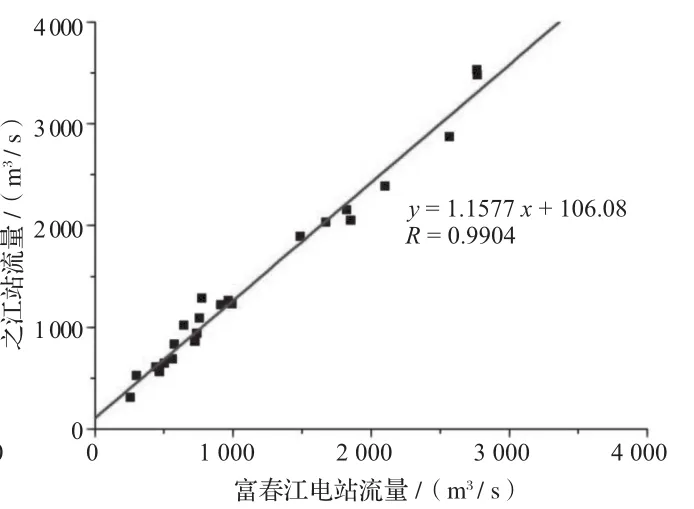
图4 2012、2014年月平均流量回归分析图（公式3）

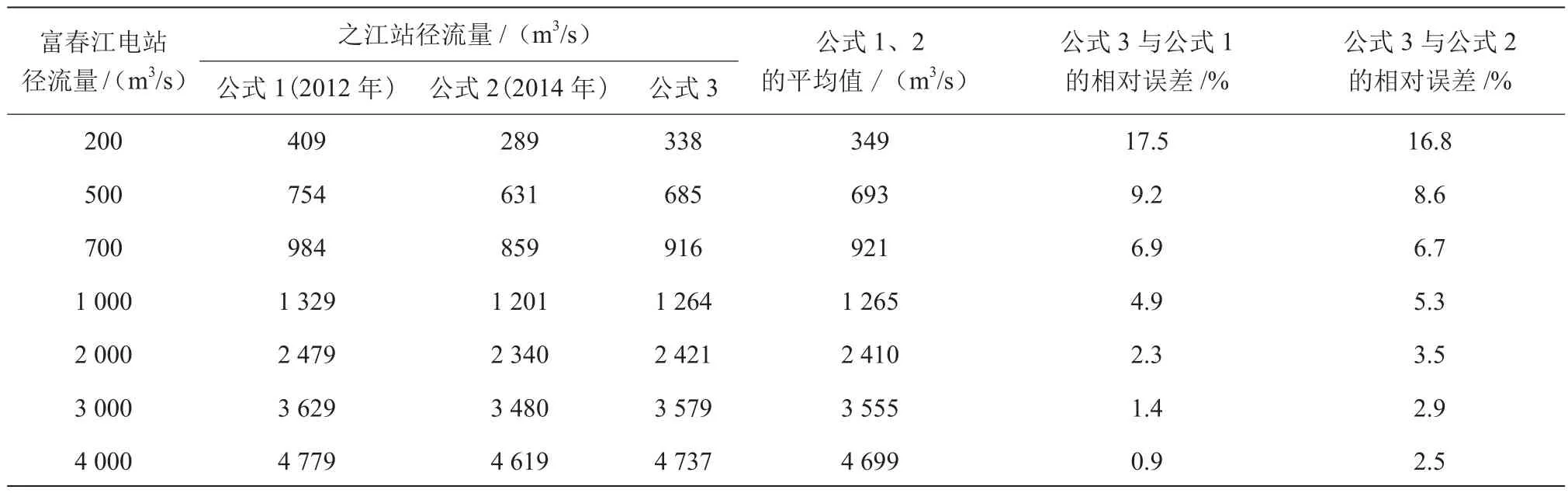
表1 采用不同拟合公式推算之江站月平均流量的误差分析表

3.2 旬平均流量回归分析

采用旬平均流量资料对之江水文站与富春江电站的径流量进行回归分析，结果见图5 ～ 7。由图5 ～ 7可知，与月平均流量的相关性相比，2站的旬平均流量相关性略有降低，但相关性仍较强，2012、2014年相关系数分别为0.9806、0.9943，汇总2 a资料回归的相关系数介于两者之间，为0.9864。

采用不同拟合公式推算之江站旬平均流量的误差分析见表2。由表2可见，旬平均流量计算结果与月平均流量计算结果的规律相似，公式6的计算值介于公式4、公式5之间，与公式4、公式5计算结果的平均值接近，流量越大，公式6的计算结果越接近于公式4的计算结果；流量越大，采用公式6计算与公式4、公式5计算结果的相对误差越小，当流量大于1 000 m3/s时，误差均小于5%。

由此可知，2站旬平均流量的相关性仍较强，基于回归公式由富春江电站的旬平均径流量推算之江水文站的旬平均径流量是可行的，建议将公式6作为计算公式。

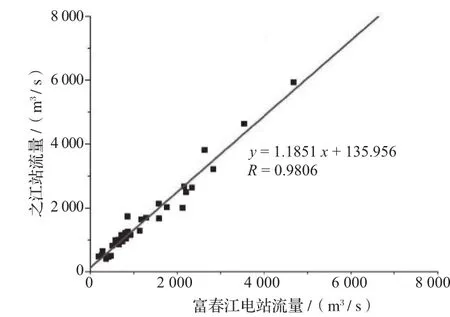
图5 2012年旬平均流量回归分析图（公式4）

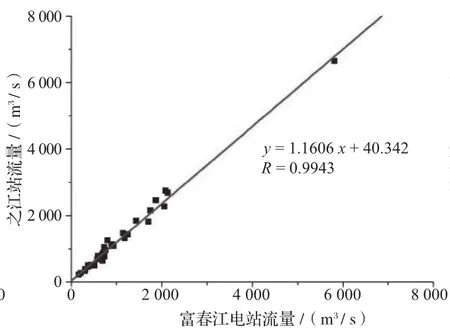
图6 2014年旬平均流量回归分析图（公式5）

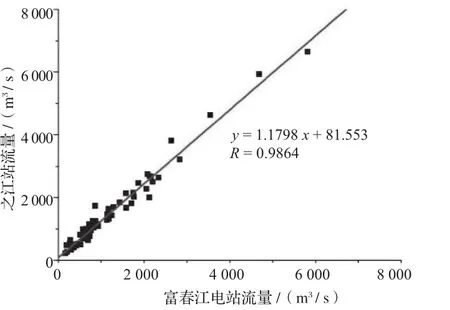
图7 2012、2014年旬平均流量 回归分析图（公式6）

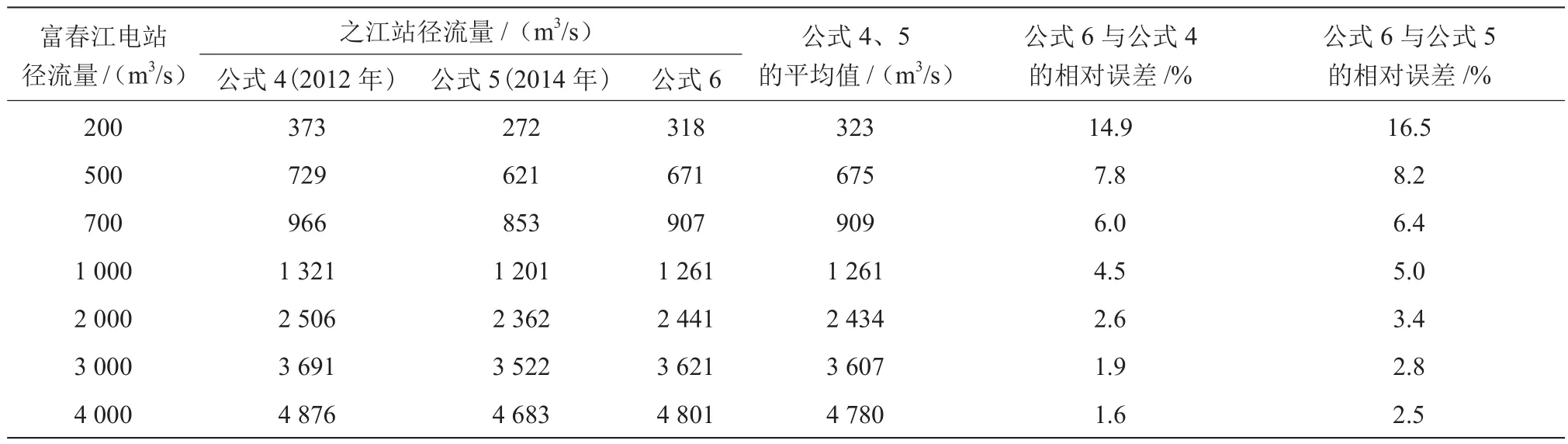
表2 采用不同拟合公式推算之江站旬平均流量的误差分析表

3.3 日平均流量回归分析

采用日平均流量资料对之江水文站与富春江电站的径流量进行回归分析，结果见图8 ～ 10。由图8 ～ 10可知，与月、旬平均流量的相关性相比，2站的日平均流量相关性显著降低，2012、2014年相关系数分别为0.9438、0.9741，汇总2 a资料回归的相关系数介于两者之间，为0.9583。导致相关性降低的原因可能有：一是钱塘江河口潮汐特性为非正规半日潮；一个涨落潮周期为12.4 h，2个涨落潮周期为24.8 h，比1 d多出约50 min，即在1 d内没有封闭完整的涨落潮过程，日平均流量没有封闭完整涨落潮周期的净下泄流量，而旬平均、月平均流量中虽然两头也未封闭完整涨落潮周期的净下泄流量，但所占比重较小；二是根据波传播速度（v）计算，富春江电站的流量波传播到之江站需5.0 ～ 6.0 h，导致富春江电站与之江站的流量峰谷有时间差，故2站短历时的流量相关性略差。

采用不同拟合公式推算之江站日平均流量的误差分析见表3。由表3可见，日平均流量的计算结果与月、旬平均流量计算结果的规律相似，公式7（2012年）、公式8（2014年）计算结果的平均值与公式9接近，流量越大，公式9的计算结果越接近于公式7的计算结果；当流量越大时，采用公式9计算与公式7、公式8计算结果的相对误差越小，当流量大于1 000 m3/s时，误差基本小于5%。

总体来说，2站日平均流量仍具有一定的相关性，若对精度要求不高，仍可基于回归公式由富春江电站的旬平均径流量推算之江水文站的日平均径流量，建议将公式9作为计算公式。

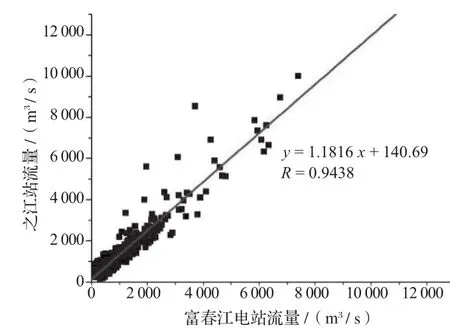
图8 2012年日平均流量回归分析图（公式7）

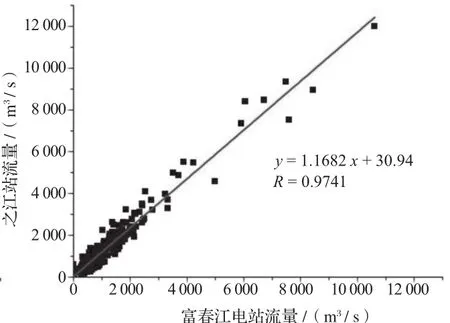
图9 2014年日平均流量回归分析图（公式8）

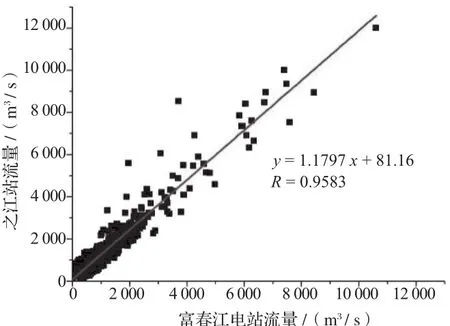
图10 2012、2014年日平均流量回归分析图（公式9）

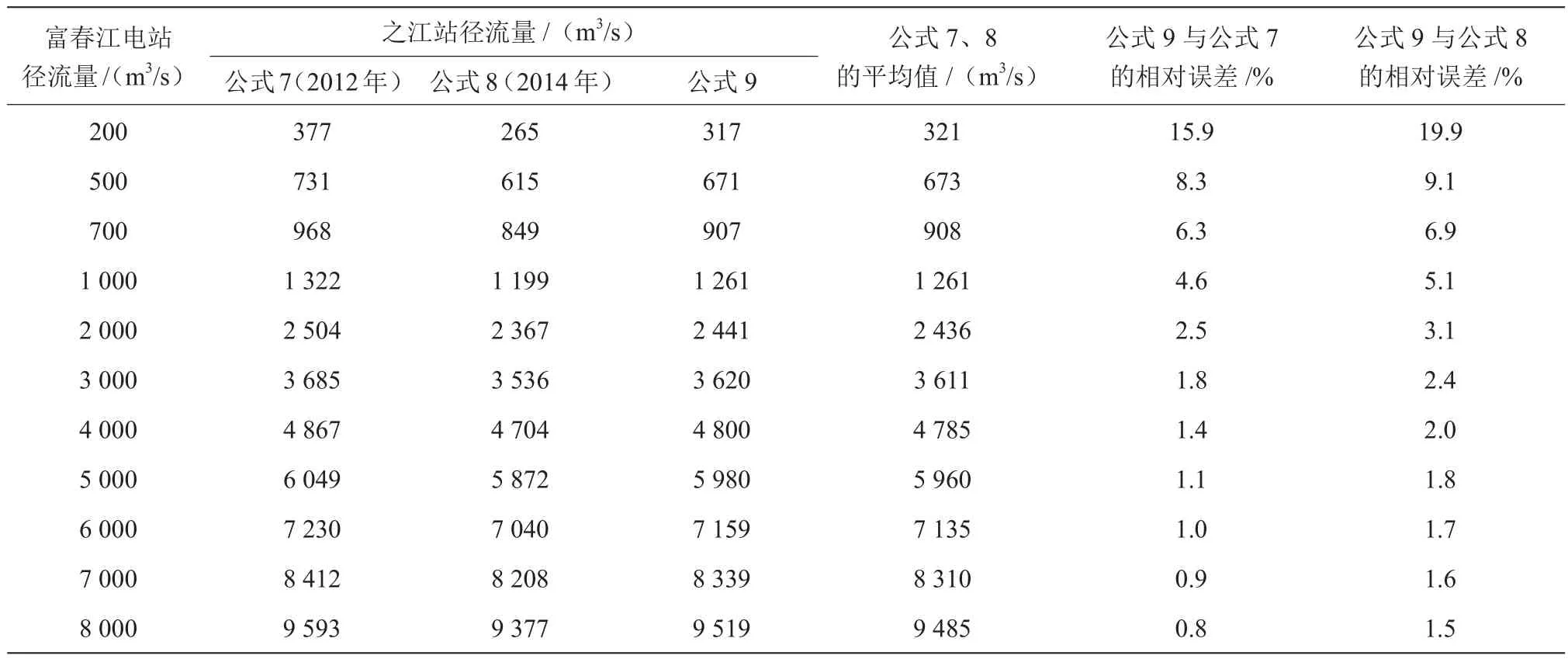
表3 采用不同拟合公式推算之江站日平均流量的误差分析表

4 结 语

采用之江水文站与富春江电站的月、旬、日平均径流量进行2站间径流量的回归分析。结果表明，月平均流量的相关性强，相关系数基本可达到0.9900以上；旬平均径流量的相关性较强，相关系数基本可达到0.9800以上；日平均径流量的相关性略差，相关系数只能达到0.9400以上。2站间日平均径流量的相关性略差可能有：一是2个涨落潮周期比1 d多出约50 min，日平均流量无法封闭完整涨落潮周期的净下泄流量；二是富春江电站的流量波与之江站的流量波有5.0 ～ 6.0 h时间差。

之江水文站的净泄流量主要由富春江下泄流量、分水江与浦阳江等区间入流以及2站之江的河道槽蓄等因素有关，关系较为复杂。本文建立相关关系仅基于实测资料分析以供延长之江水文站的水文系列，成果仅供参考。

[1] 吕耀光，黄士稳.钱塘江河口区声学多普勒测流及资料整编[J].河海大学学报(自然科学版)，2010，38(6)：682 - 687.

[2] 韩曾萃，戴泽蘅，李光炳，等，钱塘江河口治理开发[M].北京：中国水利水电出版社，2003：61 - 63.