下限温度对北京樱花盛花始期模拟效果的影响*
2018-01-31叶彩华周孝煌姜会飞姜少杰张玉莹张子源
叶彩华,周孝煌,姜会飞,姜少杰,张玉莹,张子源,李 超
下限温度对北京樱花盛花始期模拟效果的影响*
叶彩华1,周孝煌2,姜会飞2,姜少杰2,张玉莹2,张子源2,李 超3
(1.北京市气象服务中心,北京 100089;2.中国农业大学资源与环境学院,北京 100193;3.北京市气候中心,北京 100089)
利用实际物候观测资料,通过人为设定不同生长发育下限温度值,比较不同指标对应发育阶段所需积温的稳定性和物候模拟准确率,是鉴定植物生长发育下限温度指标的常用统计方法。利用1998-2014年北京市海淀区玉渊潭公园樱花盛花始期观测资料,在设定下限温度0.0~5.0℃范围内,以0.1℃为步长,分别统计历年1月1日-樱花盛花始期的阶段活动积温和有效积温,对比分析不同温度指标对两种模型阶段积温稳定性和发育期模拟准确率的影响。结果表明:(1)阶段积温随设定下限温度指标而变化,且阶段活动积温值及其年际变化值均大于有效积温;(2)两种积温的标准差以活动积温的标准差较大,表明采用有效积温测算樱花盛花始期的误差小于活动积温测算结果;阶段有效积温在设定下限温度0.0~2.9℃范围内变异系数较小,3.0℃及其以上时活动积温的变异系数小于有效积温,活动积温离散程度更小;(3)不同设定下限温度值的始花期预测结果,均以2~3℃的准确率较高。对应设定下限温度0.0~3.2℃范围,有效积温模拟始花期基本准确率(误差小于3d)和准确率(误差2d以内)均大于活动积温模拟结果,但设定下限温度>3.8℃时结果相反。设定下限温度处于3.3~3.8℃时,有效积温模拟误差的基本准确率大于活动积温,误差小于2d准确率则低于活动积温。综上所述,无论活动积温还是有效积温,均以设定下限温度2.0~3.5℃的计算结果标准差和变异系数最小,准确率较高,在未进行生理测定的条件下,可将其作为樱花盛花始期的下限温度指标。
积温;生长假设;基点温度;变异系数;模拟准确率
作物完成发育阶段所需积温基本恒定的积温理论是作物模型中广泛采用的发育期模拟预测基本原理[1]。从1735年,法国A. F.de Réaumur首次提出积温概念至今的280多年来,为提高阶段积温对作物发育进程的模拟预测准确率,阶段积温从最初简单的日均温之和,发展到基于下限温度的活动积温和有效积温[2]。自20世纪60年代作物模型创建以来,国内外作物模型中普遍使用有效积温[3-6]而极少采用活动积温[1]模拟预测作物发育进程,也缺乏对有效积温和活动积模拟预测的效果对比及有效积温优于活动积温的有力证据。
下限温度指标是作物模型中计算积温的最基本的和必需的要素,采用相同的下限温度指标,以活动积温和有效积温这两种不同的积温模型统计相同发育阶段得到的积温不同[1-8],使用相同的积温模型而采用不同的下限温度统计相同发育阶段得到的积温也不同。下限温度随作物、品种和发育期而不同,同一作物在同一发育阶段采用的下限温度也会在一定范围内波动[9-13]。准确有效的基点温度通过田间综合对比试验研究分析能测得[6,14],但受环境条件限制和温度试验方案局限的影响,通过试验研究获取基点温度[11,15]因费时费力而实施较少,所以目前作物模型应用中对基点温度常采用人为设置输入法[1-10],而不同的下限温度统计得到的阶段积温不同[15]。作物模型应用中人为设置的基点温度常被固定为某一数值[16-17],而不同的下限温度指标对发育期模拟预测效果不同[11,14,18],准确的下限温度指标是准确估算阶段积温的基础,也是影响积温模型对作物发育进程模拟和预测准确率的关键。
近年来,观赏植物的花期预测成为旅游服务的热点,物候模型被认为是模拟预测观赏植物花期的有效方法[19-20]。北京玉渊潭樱花赏花是春季游园主要活动,张爱英等[19-20]指出樱花开花下限温度范围为0~3℃,但其研究基于物候模型仅设定3℃为樱花下限温度指标,且仅计算1月1日-盛花始期的有效积温,并按阶段有效温131.7℃·d为阈值进行盛花始期预测。在基点温度范围内对比不同温度指标和不同积温模型对发育期模拟效果影响的研究尚未见报道,这是作物模型应用过程中有待进一步探索的问题。
本文拟以北京市海淀区玉渊潭公园樱花盛花始期模拟为例,基于一个下限基点温度的线性生长假设[2],统计在基点温度范围内对应下限温度指标的阶段活动积温和有效积温,对比分析下限温度对阶段积温稳定性的影响,并分析下限温度对发育进程模拟效果的影响,以期为探究有效测定基点温度的数值模拟方法和提高作物模型发育期模拟预测准确率提供科学依据。
1 材料与方法
1.1 数据资料及来源
1998-2014年樱花花期观测资料由北京玉渊潭公园管理处提供,盛花始期定义为观测树木1/3以上的花蕾展开花瓣的初始日期。地面气象站1998-2014年逐日平均气温数据由北京市气象局提供。
1.2 研究方法
1.2.1 线性生长假设
作物发育阶段的积温(Growing degree days,GDD)统计均为基于作物生长发育速率对温度反应的生长假设,目前较流行的生长假设分为线性假设和优化假设两大类[2,7],应用最广且最简单的一种是基于一个下限基点温度的线性生长假设,即以温度高于生物学下限温度时启动生长发育为前提,假定在温度等于或低于下限温度时生长发育速率为0;当温度高于下限温度时,生长发育速率随温度的增加而线性增加[8,12]。本研究基于这种线性生长假设统计阶段积温。
1.2.2 阶段积温计算方法
基于线性假设统计阶段连续n天(i=1, 2, 3, …, n)的活动积温(GDD,GDDA)和有效积温(Effective GDD,GDDE),阶段积温计算方法为
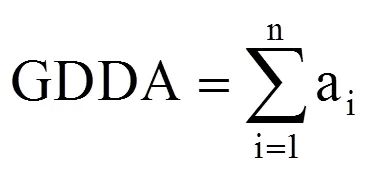
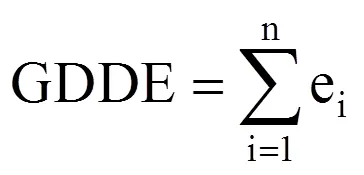
式中,活动温度ai和有效温度ei计算方法为
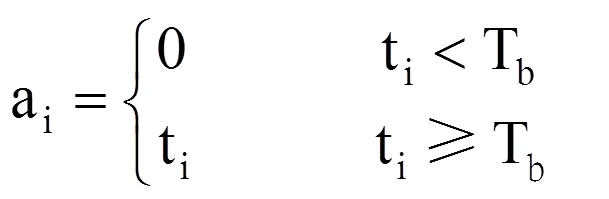
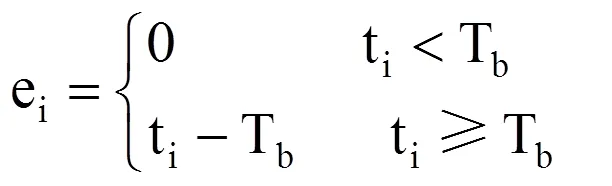
式中,ti表示计算阶段内逐日日平均气温(℃);Tb表示该生育阶段作物生长的下限(基点)温度(℃)。
本文以樱花花期的下限温度3℃[19-20]为中心,综合文献资料[19]适度扩大温度范围至0~5℃,以0.1℃为温度步长,统计不同下限温度对应的1月1日-盛花始期的阶段活动积温和有效积温。
1.2.3 检验指标
(1)标准差。标准差(SD)也称标准偏差,描述样本序列各数据偏离平均值的距离(离均差)的平均数,即
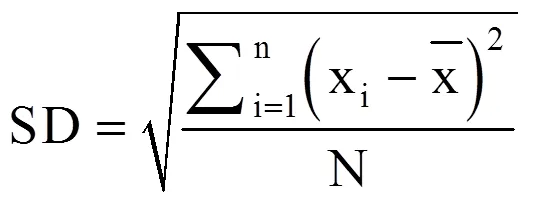
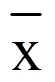
(2)变异系数。变异系数(CV)表达样本序列相对离散程度,是标准差与平均值之比,表达式为
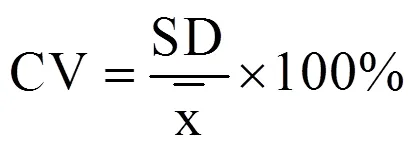
统计变量的变异系数越小,说明数据序列稳定性越大。分别统计对应下限温度指标的阶段活动积温和有效积温的变异系数,分析下限温度指标对阶段积温相对稳定性的影响。
(3)均方根误差。均方根误差(RMSE)是作物模型中普遍采用的检验模拟值与观测值偏离程度的统计量[1],计算式为
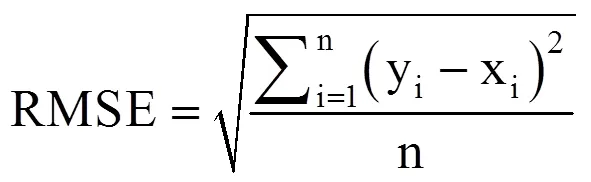
式中,xi和yi分别表示历年发育期的实测值和模拟值,发育期用阶段时间表示,即从发育初始日-终日前一天所持续的天数。均方根误差越大,表示模拟值与观测值偏离越大,即模拟效果越差;反之模拟效果越好。
(4)模拟准确率。以对应下限温度统计的多年平均阶段积温为基准,从1月1日起往后推移统计积温,当积温达到或超过基准值时的当日即为开花日,第2日即为盛花始期。1月1日-盛花始期持续天数即为积温模型模拟的阶段发育天数。
模拟准确率(accuracy of simulation,AS)是检验模型模拟效果的指标,以模拟结果与实况相符的数量n0占总样本数n的百分率(%)表示,即
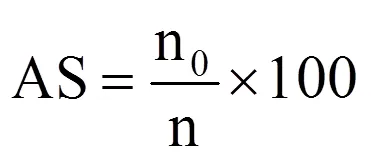
式中,n0表示按积温模型模拟的阶段发育天数与实际观测值相符的年数。本文分别统计模拟值与实际值两者之差绝对值小于3d(定义误差在3d之内)的基本准确率,两者之差绝对值小于2d(误差在3d之内)的准确率,以及模拟与实际完全一致(误差为0d)的绝对准确率3种情形。
2 结果与分析
2.1 阶段积温随下限温度设定值的变化
依据式(1)和式(4),在设定的下限温度范围0.0~5.0℃内,以0.1℃为步长分别统计1998-2014年北京市海淀区玉渊潭公园1月1日-樱花盛花始期的历年对应下限温度指标的阶段活动积温(GDDA)和有效积温(GDDE),该阶段积温多年平均值(GDDm)、最大值(GDDx)和最小值(GDDn)随下限温度设定值(Tbs)的变化如图1。由图可见,阶段积温随下限温度设定值而变化,对应设定的下限温度,阶段活动积温值及年际变化值均大于有效积温。具体表现为:(1)下限温度设定范围在0.0~5.0℃,活动积温和有效积温随下限温度的升高而减少,且有效积温减少速率比活动积温快;(2)活动积温多年平均值(198.4~254.3℃·d)、最大值(229.2~315.2℃·d)和最小值(164.8~226.0℃·d)分别大于对应下限温度有效积温的平均值(84.9~254.3℃·d)、最大值(102.9~315.2℃·d)和最小值(59.7~226.0℃·d),对应两者差值随着下限温度的升高而呈现上下波动的增大趋势,活动积温和有效积温平均相差113.5℃·d(105.1~126.3℃·d);(3)阶段活动积温和有效积温都存在明显的年际变化,且活动积温年际变化(60.0~89.8℃·d)较有效积温的(33.0~89.2℃·d)大,活动积温的平均值(76.8℃·d)比有效积温的平均值(49.2℃·d)高27.6℃·d;(4)阶段积温年际变化随下限温度上下波动,活动积温年际间变化最小值为60.0℃·d(对应下限温度4.3~4.4℃),大于有效积温年际间变化最小值33.0℃·d(对应下限温度2.9~3.0℃)。
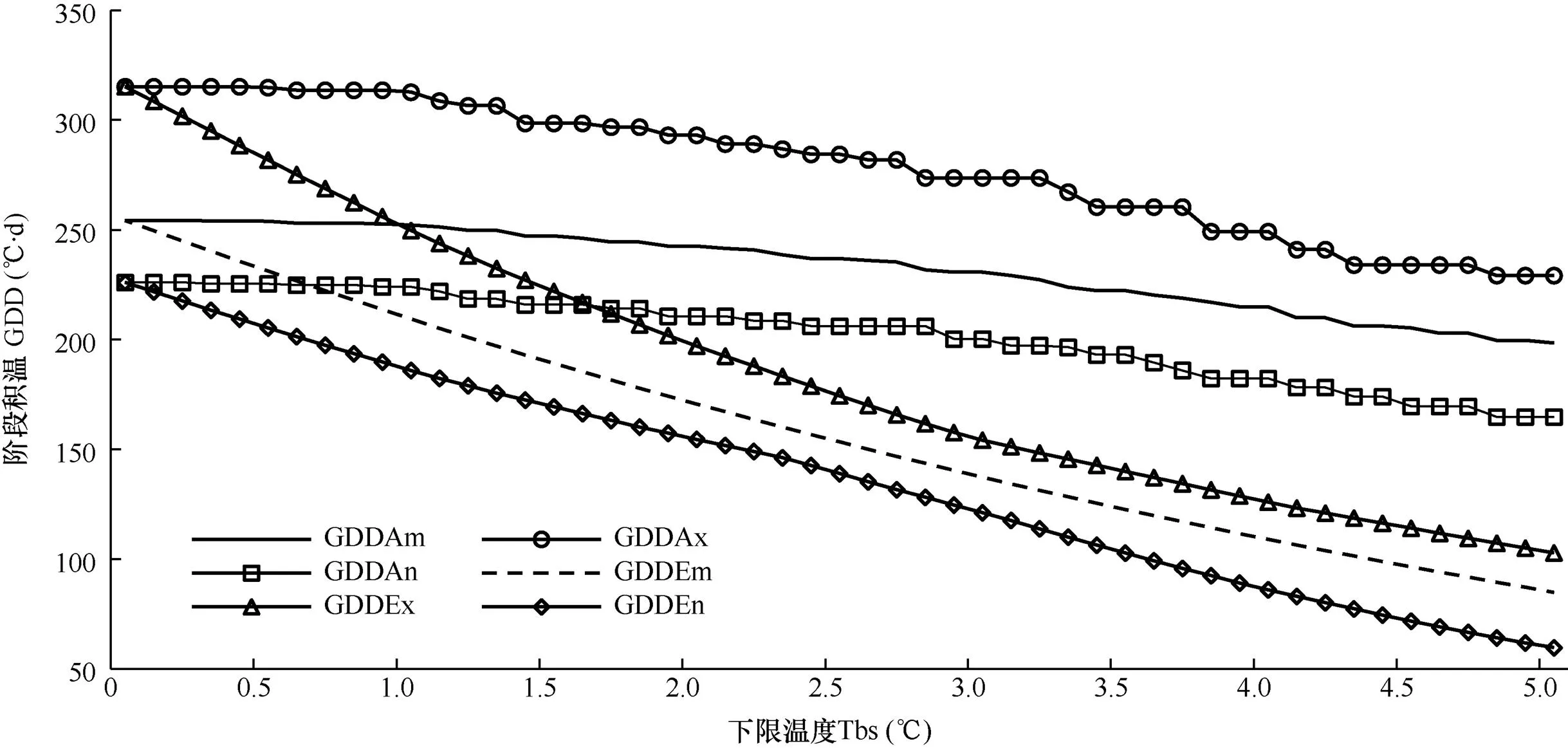
图1 1998-2014年樱花阶段积温(GDD)平均值和极值随下限温度设定值的变化
注:GDDAm、GDDAx、GDDAn分别为活动积温平均值、最大值和最小值。GDDEm、GDDEx、GDDEn分别为有效积温平均值、最大值和最小值
Note: GDDAm, GDDAx, GDDAn are average, maximum and minimum values of active GDD, respectively, while GDDEm, GDDEx and GDDEn are mean, maximum and minimum of effective GDD, respectively
2.2 下限温度设定值对阶段积温稳定性的影响
2.2.1 对标准差的影响
根据式(5)和式(6)分别计算对应不同下限温度设定值1998-2014年1月1日-樱花盛花始期的阶段活动积温(GDDA)和有效积温(GDDE)数据序列的标准差(standard deviation,SD)和变异系数(coefficient of variation,CV)。由图2可以看出,阶段积温的稳定性随下限温度设定值而变化。从表征阶段积温绝对稳定性的标准差来看,在下限温度设置范围0.0~5.0℃内,阶段活动积温和有效积温的标准差平均值为19.2℃·d和12.9℃·d,表明采用有效积温测算樱花始期的误差要小于活动积温测算结果。两种积温的标准差都有先随下限温度升高而减小,然后随温度升高而升高的总趋势,但活动积温的标准差变化呈现上下波动,而有效积温的标准差随温度变化曲线相对平滑。在0.0~2.6℃范围内,有效积温标准差随温度升高而快速下降,从21.8℃·d降至10.8℃·d,在2.7~5.0℃温度范围则随温度升高而缓慢升高至11.7℃·d。而阶段活动积温在0.0~2.6℃范围标准差随温度升高呈现波动下降趋势,从21.3℃·d波动降至17.3℃·d,变化速率为1.54℃·d·℃-1,较有效积温的4.04℃·d·℃-1相对缓和;在2.7~5.0℃温度范围则随温度升高而相对缓慢地波动上升至21.2℃·d,变化速率为1.63℃·d·℃-1,较有效积温的0.34℃·d·℃-1相对要快。
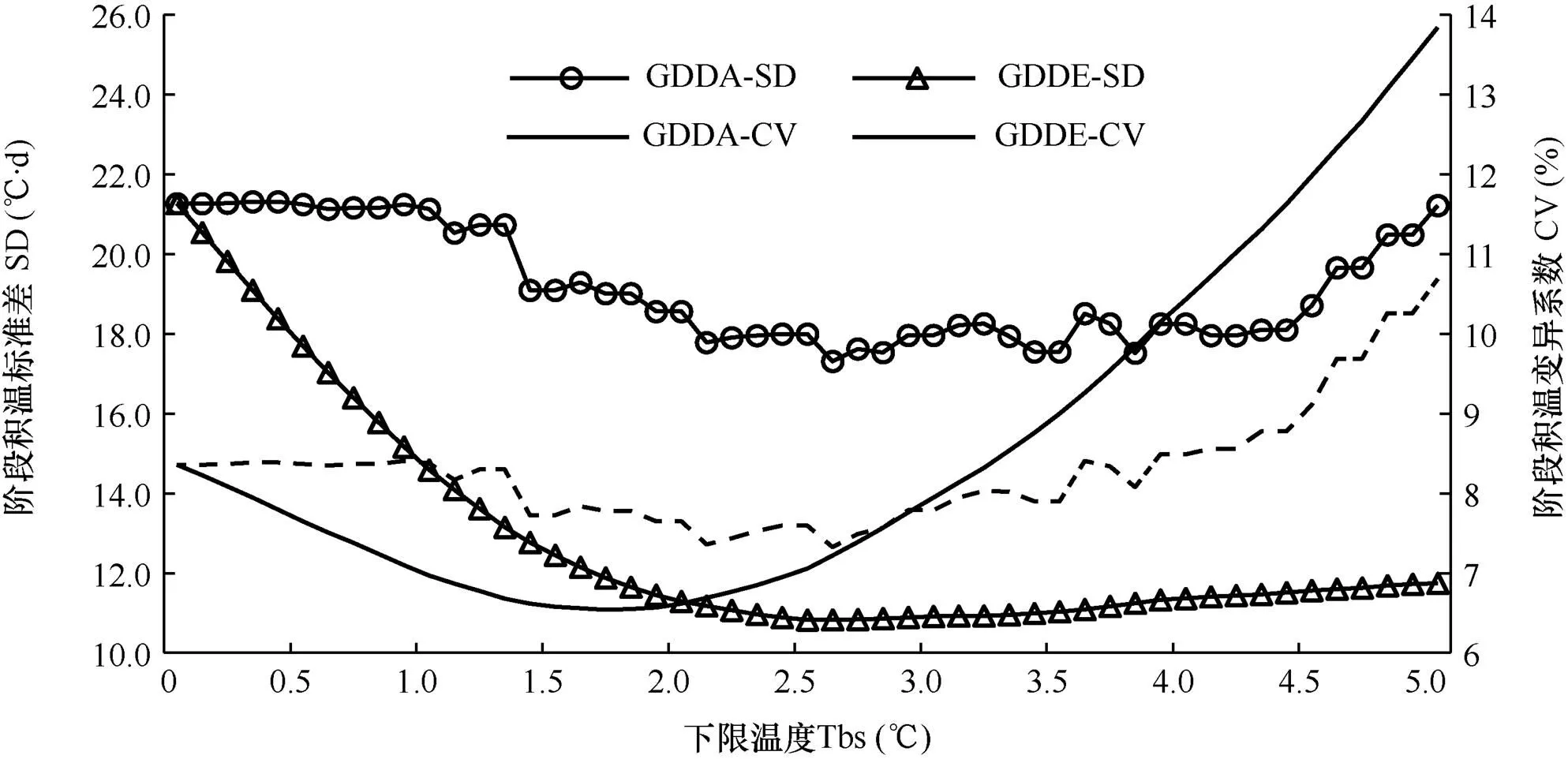
图2 阶段活动积温和有效积温的标准差(SD)和变异系数(CV)随下限温度设定值的变化
2.2.2 对变异系数的影响
从表征相对稳定性的变异系数来看,下限温度设定在3.0℃以下时活动积温变异系数大于有效积温,当下限温度在3.0℃及其以上时有效积温变异系数则大于活动积温,这表明以0~2.9℃设置下限温度时,有效积温比活动积温相对更加稳定,而以3.0~5.0℃设置下限温度时,活动积温则较有效积温稳定;在下限温度设置范围0.0~5.0℃内,活动积温变异系数在7.33%~10.69%波动,历年阶段活动积温变异系数最小(7.33%)和次小(7.36%)对应的下限温度分别为2.6℃和2.1℃,且下限温度在1.4℃~3.1℃范围内的阶段活动积温变异系数较小(7.33%~7.95%),且基本稳定在8.0%以下;阶段有效积温变异系数随下限温度指标的变化曲线比活动积温的相对平滑,在0.0~1.7℃范围内变异系数随温度降低而减小,在1.7~5.0℃范围内随温度升高而增大,1.7℃对应的变异系数最小(6.54%),0.7~2.7℃范围内阶段有效积温变异系数较小(6.54%~7.38%),且在0.3~3.0℃范围内变异系数基本稳定在8.0%以下。
可见,无论活动积温还是有效积温,都以设定下限温度2.0~3.5℃范围内的计算结果标准差和变异系数最小,因此,在未进行生理测定的情况下,2.0~3.5℃可作为樱花盛花始期的下限温度指标。
2.3 不同下限温度设定值对盛花始期模拟效果的影响
2.3.1 对均方根误差的影响
以对应下限温度统计的多年平均阶段积温为基准,从1月1日起往后推移统计积温,当积温达到或超过基准值时的当日即为开花日,开花日往后推一天即为模拟盛花始期开始,根据式(7)计算模拟发育期与实际发育期的均方根误差,并绘制阶段活动积温和有效积温的均方根误差(RMSE)。从图3可以看出,对应模拟均方根误差的最小值(1.25d)的下限温度在1.8~2.1℃范围内,而在0.0~1.8℃范围内,有效积温的模拟均方根误差(1.25~1.79d)随着下限温度的升高逐渐减小,说明模拟效果随下限温度升高而更接近实际值,在2.1~5.0℃范围内随着温度升高模拟值逐渐偏离实际值(1.25~2.31d);活动积温的模拟均方根误差(1.44~1.85d)随着温度变化呈现微小的上下波动;其中,活动积温模拟均方根误差最小值(1.44d)对应的下限温度为2.8℃。
在下限温度小于3.3℃时,对应的阶段有效积温模拟的均方根误差(RMSE-GDDE)都比活动积温的(RMSE-GDDA)小,表明下限温度在0~3.2℃范围内有效积温模拟效果优于活动积温,而当下限温度在3.2℃以上时,活动积温模拟效果优于有效积温。
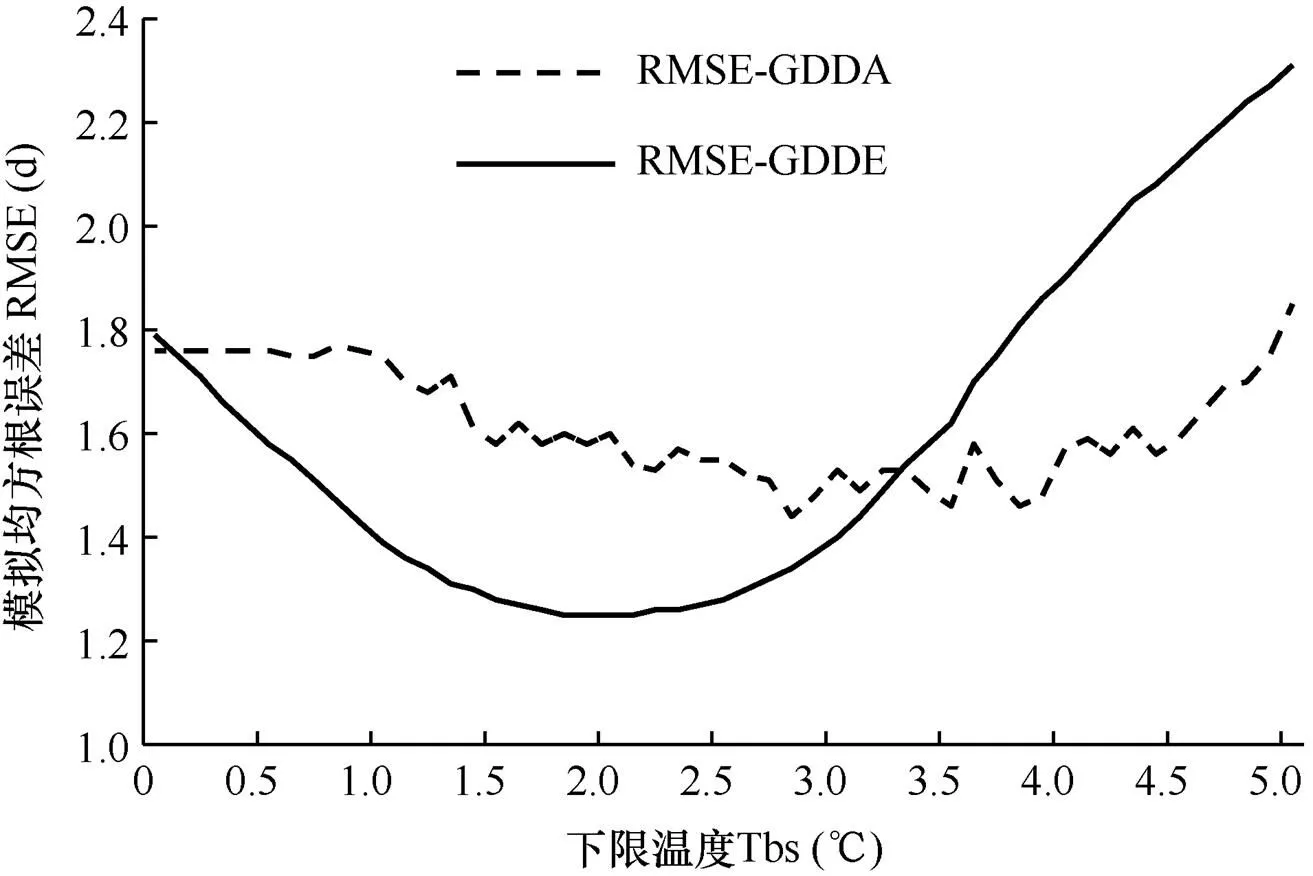
图3 活动积温(GDDA)和有效积温(GDDE)模拟的盛花始期均方根误差随下限温度的变化
2.3.2 对模拟准确率的影响
以均方根误差进行模拟效果比较时,统计的是多年模拟值与实际偏差的平均情况,在实际应用中,根据式(8)分别统计历年模拟与实际对比结果的准确率更有实际指导价值。以AS-GDDA-3、AS-GDDA-2、AS-GDDA-0和AS-GDDE-3、AS-GDDE-2、AS-GDDE-0分别表示按阶段活动积温和有效积温模拟阶段发育天数与实际发育天数误差在3d内的基本准确率、2d内的准确率和无偏差的绝对准确率,相应阶段积温模拟效果随下限温度变化情况如图4所示。从图可知,阶段活动积温和有效积温对应的3种准确率均随着设定的下限温度而变化。当下限温度在0.0~4.3℃时,两种积温模型的模拟准确率和基本准确率都在82.4%以上,但准确率的大小有所不同,下限温度在0.0~3.2℃之间,有效积温模拟的基本准确率和准确率均大于或等于活动积温的;在3.3~3.8℃时,有效积温的基本准确率大于活动积温的,而模拟准确率则小于活动积温的;在3.8~4.3℃时,有效积温的模拟准确率和基本准确率则小于活动积温的。当下限温度高于4.3℃时,仅有效积温的模拟准确率降至70.6%~76.5%,且活动积温的模拟准确率和基本准确率均大于有效积温的。绝对准确率在设置的下限温度范围内均低于38%,在两种积温模型下的大小变化较复杂。
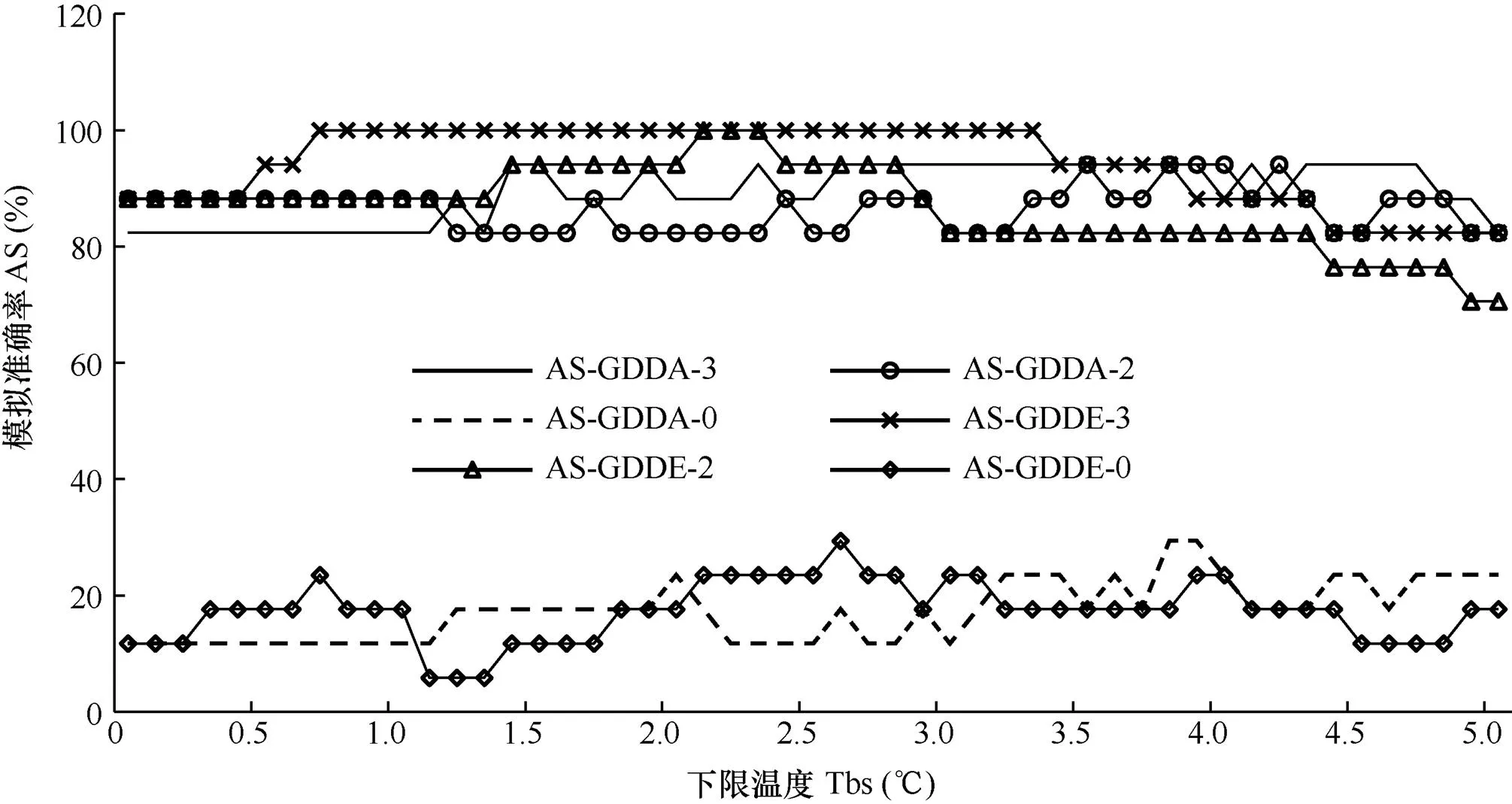
图4 活动积温和有效积温对发育期的模拟准确率(AS)随下限温度的变化
可见,在下限温度不确定的情况下,人为设定下限温度利用阶段积温模拟预测植物发育进程时,模拟预测效果随下限温度和积温模型而异。结合阶段积温稳定性统计分析推测下限温度范围为2.0~3.5℃,而以此范围的下限温度计算的阶段积温进行发育期模拟预测时,活动积温和有效积温的模拟效果随下限温度设定值而异,在具体工作中要因地制宜掌握。
对照阶段发育天数来看,北京玉渊潭樱花1998-2014年阶段发育天数为76(2002年)~100d(2010年)。阶段积温最大的年份(1999年)并没有出现在发育天数最长的年份,阶段积温最小值出现的年份(2012年)也不是发育天数最短的年份。阶段发育天数变异系数6.9%,标准偏差6.1d,阶段发育天数平均为88.1d,按阶段平均天数模拟发育期的基本准确率、准确率和绝对完全准确率分别为41.2%、17.6%和5.9%。无论是阶段活动积温还是有效积温对玉渊潭樱花始期模拟效果都明显优于以平均阶段发育天数对发育期的模拟,因此运用阶段积温模拟预测发育进程仍然是国内外特别是作物模型中普遍采用的基本方法。
3 讨论与结论
(1)阶段积温随设定下限温度变化而变化,相同下限温度的阶段活动积温高于有效积温;阶段活动积温和有效积温均具有明显的年际变化,且活动积温的年际变化大于有效积温。
(2)阶段积温的标准偏差和变异系数随下限温度而变化,相同下限温度的有效积温的标准偏差均小于活动积温的;以标准偏差分析阶段积温的绝对稳定性时,有效积温优于活动积温;以变异系数分析阶段积温相对稳定性时,下限温度在3.0℃以下时阶段有效积温比活动积温稳定,下限温度在3.0℃及其以上时活动积温较有效积温稳定。
(3)以均方根误差评判发育期模拟效果,当设定下限温度小于3.2℃时,阶段有效积温的模拟效果比活动积温好,当下限温度在3.2℃以上时活动积温模拟效果优于有效积温;以发育期模拟值与实际值偏差在2d和3d表征模拟准确率和基本准确率时,设定下限温度在0.0~3.2℃范围内,有效积温的模拟准确率和基本准确率均大于活动积温;下限温度大于3.8℃时,有效积温的模拟准确率和基本准确率小于活动积温;当下限温度在3.3~3.8℃时,有效积温的基本准确率大于活动积温,而其模拟准确率则小于活动积温的。
在设定下限温度3.0~5.0℃时,阶段活动积温比有效积温变异系数小、年际间相对稳定和对发育期模拟效果与实际值更相符,这些特点与现行科技文献特别是作物模型中普遍采用有效积温模拟预测发育进程相悖[1]。这是因为基于日均温统计阶段积温时,忽视了温度日变化的事实。当发育阶段中某日的日均温等于或低于下限温度时,按积温统计规则,则该日热量对阶段积温贡献数值为零,但该天中存在一段时间内高于下限温度的温度,这一时段的温度对生长发育是有效的,但却在统计模型中被忽略,因此,为提高作物模型的适用性和有效性,可用时积温改进积温模型[2,7,21-22]。
不同作物品种其基点温度不同,界限温度随品种波动较大,并且在植物的实际发育过程中,下限温度也不是一成不变的,发育速率随温度上升也不一定总是保持线性关系[12]。以温度模拟发育进程的模型只是一个近似模拟发育进程的统计模型,并非真正的生物生理过程,准确有效的作物品种基点温度是要通过实验和试验获得的。因此,在应用作物模型模拟预测发育进程时,如果缺乏通过作物品种在当地的试验研究中得到的下限温度指标,基点温度不准确,建议用作物模型对比活动积温和有效积温的模拟结果,分析不同温度指标对阶段积温稳定性和模拟效果的影响,根据研究区域观测数据的计算和检验结果,探寻阶段积温相对稳定和模拟效果较好的积温模型,提取相对有效的基点温度指标,而不是单一选用有效积温或基点温度。另一方面,目前的作物模型采用考虑两个、三个或四个基点温度指标的生长假设的研究已较为常见,而本研究仅从基于下限温度的线性生长假设的积温模型进行阶段积温统计和发育期模拟效果对比分析,综合比较多种生长假设的积温模型的阶段积温稳定性和模拟效果是有待深入研究的课题,多基点温度指标对积温模型的影响有待进一步探究。
此外,影响作物发育进程的因素繁多,主要有生物因素和环境因素。前者是内在因素,包括物种及品种类型、生理控制等;后者是外在因素,包括温度、光照、水分和生长调节剂等,甚至病虫害和其它灾害对发育进程也有影响[22],但其中气温、光照、水分为主要影响因子,如光周期,在早春气温偏低年份,开花虽然偏迟,但在延长的日照长度促进下,达到始花期所需积温可以比正常年和春暖年偏少。本研究仅基于积温理论以温度为单一因素模拟发育进程,也可能引起模拟失真而产生偏差和误差。因此,深入生长发育与环境因子关系的机理性研究,综合环境因子中有利条件对生长发育的正面影响和不利条件的负作用,是今后改进本研究中的作物模型,以提高发育期模型模拟预测准确率和提高作物模型应用性需努力的方向。
[1]吴玉洁,叶彩华,姜会飞,等.不同积温计算方法作物发育期模拟效果比较[J].中国农业大学学报,2016,21(10): 117-126.
Wu Y G,Ye C H,Jiang H F.Comparison of the simulation effect of different growing degree-days calculating methods on crop development processes[J].Journal of China Agricultural University, 2016,21(10): 117-126.(in Chinese)
[2]姜会飞,温德永.基于线性生长假设利用极端温度计算日积温的方法[J].中国农业大学学报,2013,18(1):82-87.
Jiang H F,Wen D Y.Methods of calculating growing degree-day based on LR assumption and daily extreme temperatures[J]. Journal of China Agricultural University,2013,18(1):82-87.(in Chinese)
[3]Mcmaster G S,Wilhelm W W,Palic D B,et al.Spring wheat leaf appearance and temperature:extending the paradigm[J]. Annals of Botany,2003,91(6):697-705.
[4]Theodore C H,Lee H,Pasquale S,et al.AquaCrop:the FAO cropmodel to simulate yield response to water III:parameterizationand testing for maize[J].Agronomy Journal,2009,101:448-459.
[5]Aiken R M.Applying thermal time scales to sunflower development [J].Agronomy Journal,2005, 97:746-754.
[6]Mcmaster G S,White J W,Hunt L A,et al.Simulating the influence of vernalization,photoperiod and optimum temperature on wheat developmental rates[J].Annals of Botany,2008,102: 561-569.
[7]姜会飞,温德永.基于优化生长假设利用极端温度计算日积温的方法[J].中国农业大学学报,2013,(2):116-123.
Jiang H F,Wen D Y.Methods of calculating growing degree-day based on OR assumption and daily extreme temperatures[J]. Journal of China Agricultural University,2013,(2):116-123.(in Chinese)
[8]Mcmaster G S,Wilhelm W W.Growing degree-days:one equation, two interpretations[J].Agricultural and Forest Meteorology, 1997,87(4):291-300.
[9]康西言,董航宇,姚树然.基于气象因子的冬小麦发育期预报模型[J].中国农业气象,2015,36(4):465-471.
Kang X Y,Dong H Y,Yao S R.Prediction model of winter wheat development stages based on meteorological factors[J]. Chinese Journal of Agrometeorology,2015,36(4):465-471.(in Chinese)
[10]Jenni S,Bourgeois G,Laurence H,et al.Improving the prediction of processing bean maturity based on the growing degree day approach[J].Hortscience A Publication of the American Society for Horticultural Science,2000,35(4):611-614.
[11]Moreno L S B,Pedreira C G S,Boote K J,et al.Base temperature determination of tropical Panicum spp.grasses and its effects on degree-day-based models[J].Agricultural and Forest Meteorology, 2014,186:26-33.
[12]姜会飞.农业气象学(第二版)[M].北京:科学出版社, 2013: 70-71.
Jiang H F.Agrometeorology (second edition)[M].Beijing: Science Press,2013:70-71.(in Chinese)
[13]Porter J R,Gawith M.Temperatures and the growth and development of wheat:a review[J]. European Journal of Agronomy,1999,10(1):23-36.
[14]Vinocur M G,Ritchie J T.Maize leaf development biases caused by air-apex temperature difference[J].Agronomy Journal, 2001,(93):767-772.
[15]王晓霞,冯雪菲,张富荣.朝阳地区近50年生长季小麦有效积温变化特征分析[J].中国农学通报,2014,30(2):280-285.
Wang X X,Feng X F,Zhang F R.Variation characteristic of effective accumulated temperature during wheat growth season in Chaoyang area in recent 50 years[J].Chinese Agricultural Science Bulletin,2014,30(2):280-285.(in Chinese)
[16]Tian Z,Zhong H L,Sun L X,et al.Improving performance of Agro-ecological zone(AEZ) modeling by cross-scale model coupling:an application torice production in Northeast China[J].Ecological Modelling,2014,290:155-164.
[17]Bocchiola D,Nana E,Soncini A.Impact of climate change scenarios on crop yield and water footprint of maize in the Po valley of Italy[J].Agricultural Water Management,2013, 116:50-61.
[18]Herrmann A,Kornher A,Taube F.A new harvest time prognosis tool for forage maize production in Germany[J]. Agricultural and Forest Meteorology,2005,130: 95-111.
[19]张爱英,王焕炯,戴君虎,等.物候模型在北京观赏植物开花期预测中的适用性[J].应用气象学报,2014,25(4):483-492.
Zhang A Y,Wang H J,Dai J H,et al.Applicability analysis of phonological models in the flowering time prediction of ornamental plants in Beijing area[J].Journal of Applied Meteorological Science,2014,25(4):483-492.(in Chinese)
[20]张爱英,张建华,高迎新,等.SW物候模型在北京樱花盛花始期预测中的应用[J].气象科技,2015,43(2):309-313.
Zhang A Y,Zhang J H,Gao Y X,et al.Prediction of first flowering date ofin Beijing Yuyuantan Park using phonological model[J].Meteorological Science and Technology, 2015,43(2):309-313.(in Chinese)
[21]Rodriguez-Rajo F J,Frenguelli G,Jato M V.Effect of air temperature on forecasting the start of thepollen season at two contrasting sites in the south of Europe (1995-2001) [J].International Journal of Biometeorology, 2003,47: 117-125.
[22]喻莎,陆魁东,谢佰承,等.高温时数和热积温对超级早稻结实率的影响[J].中国农业气象,2016,37(4):454-463.
Yu S,Lu K D,Xie B C,et al.Effects of high temperature hours and thermal accumulated temperature on seed setting rate of super hybrid rice[J].Chinese Journal of Agrometeorology, 2016,37(4):454-463.(in Chinese)
Impacts of Different Base Temperature on Simulation Effect of Beginning Flowering Date ofin Beijing
YE Cai-hua1, ZHOU Xiao-huang2, JIANG Hui-fei2, JIANG Shao-jie2, ZHANG Yu-ying2, ZHANG Zi-yuan2, LI Chao2
(1.Beijing Meteorological Service Center, Beijing 100089, China; 2.College of Resource and Environment Sciences, China Agriculture University, Beijing 100193; 3. Beijing Regional Climate Center, Beijing 100089)
It is a commonly used statistical method to determine the base temperature index (Tb) of plant growth and development by comparing stability and prediction accuracy of stage growing degree days (GDD) calculated by different artificial given base temperature index using actual observed phenomena data.In this paper, active growing degree days (GDDA) and effective growing degree days (GDDE) from Jan. 1st to the beginning flowing date ofwere calculated by different given Tb in the range of 0.0-5.0 ℃ with step of 0.1℃ using the observed data during 1998-2014 at Yuyuantan Park, Haidian District, Beijing. Effects of different given Tb on stability of two kinds GDD and simulated phenomena accuracy were also compared and analyzed. The results showed that: (1)stage GDD changes as Tb changes. GDDA and its inter-annual variability are both bigger than that of GDDE.(2)Both standard deviation (SD) and coefficient of variation (CV) of calculated GDDA or GDDE are smallest at the Tb range of 2.0-3.5℃, which could be the real Tb ofdetermined by statistics under the condition without physiological experiment. SD of GDDA is bigger than that of GDDE, suggested that error of the beginning flowing date estimated by GDDE is smaller than that by GDDA. As an index of relative discrete degree, CV of GDDE calculation is smaller than that of GDDA in the Tb range of 0.0-2.9℃ but is bigger if Tb ≥3.0℃.(3)Comparing estimated beginning flowing dates of different given Tb, the accuracy is highest in the range of 2-3℃. In the range of 0.0-3.2℃, both basic accuracy (error<3days) and accuracy (error<2days) of the simulated date by GDDE is better than that by GDDA, but is opposite when Tb>3.8℃.In the range of 3.3-3.8℃, basic accuracy estimated by GDDE is better than that of GDDA, but accuracy is opposite.
Growing degree-days;Growth and developmental assumption;Base temperature; Coefficient of variation;Simulation accuracy
10.3969/j.issn.1000-6362.2018.01.001
叶彩华,周孝煌,姜会飞,等.下限温度对北京樱花盛花始期模拟效果的影响[J].中国农业气象,2018,39(1):1-8
2017-08-07
国家重点研发计划课题“主要粮食作物气象灾害发生规律及指标研究”(2017YFD0300401);北京市财政专项“2017年气象为农—都市生态休闲农业气象科技支撑服务”
叶彩华(1968-),女,研究员,从事农业气候研究和应用服务。E-mail:ych681012@126.com
