CMM测量中基于确定采样策略的圆锥面拟合方法*

张 俐， 郭超朋， 刘京亮

(1. 北京航空航天大学 机械工程及自动化学院， 北京 100191； 2. 北京航空精密机械研究所， 北京 100076)

随着制造业数字化、智能化发展， 机械制造对零部件特征高效、高精度检测的要求逐步提高. 三坐标测量是精密检测的一种重要方式， 广泛应用于机械零部件测量. 圆锥面作为机械零件表面常见的二次曲面， 相对于平面、球、圆柱等二次曲面拟合， 圆锥面拟合参数多， 距离函数复杂且拟合初值计算困难.

对于标准二次曲面， 多采用数值迭代优化计算方法拟合. 在数值迭代优化拟合中， 初值计算[1]、距离函数模型及优化方法的选择对拟合结果准确性影响较大. 研究人员利用不同初值计算方法获取拟合初值并进行迭代优化拟合. 李岸[2]、刘元朋[3]等利用锥面的单位法矢形成的高斯映像计算拟合初值， 需计算各数据点法矢,计算较复杂且精度有限. 梁爽[4]等利用待拟合标准二次曲面周围的平面与其位置约束关系计算拟合初值， 该方法利用工件多表面位置约束关系， 但其计算受工件表面情况限制.

Lukács G[5]等提出利用“忠实距离”取代空间数据点到曲面“真实距离”的二次曲面拟合方法， 该方法具有代表性. 但Lukács G仅使用随机选取的不超过4个点位置与法矢估算二次曲面的几何参数初值， 可靠性很低， 易导致算法收敛慢， 或收敛于局部最小值[1].

几何参数初值选取对非线性距离目标函数优化能否收敛至全局最优点是至关重要的. 三坐标测量采样策略是确定工件尺寸是否符合既定设计标准和规格的关键， 采样获取信息量取决于采样点数量和采样数据波动[6]. 因此本文提出基于确定采样策略的圆锥面拟合方法,根据确定的采样策略可靠估计圆锥面几何参数初值， 结合Benk″P[7]等提出的圆锥面距离函数模型逼近函数表达式， 精确计算圆锥面几何参数.

1 圆锥面距离函数参数化

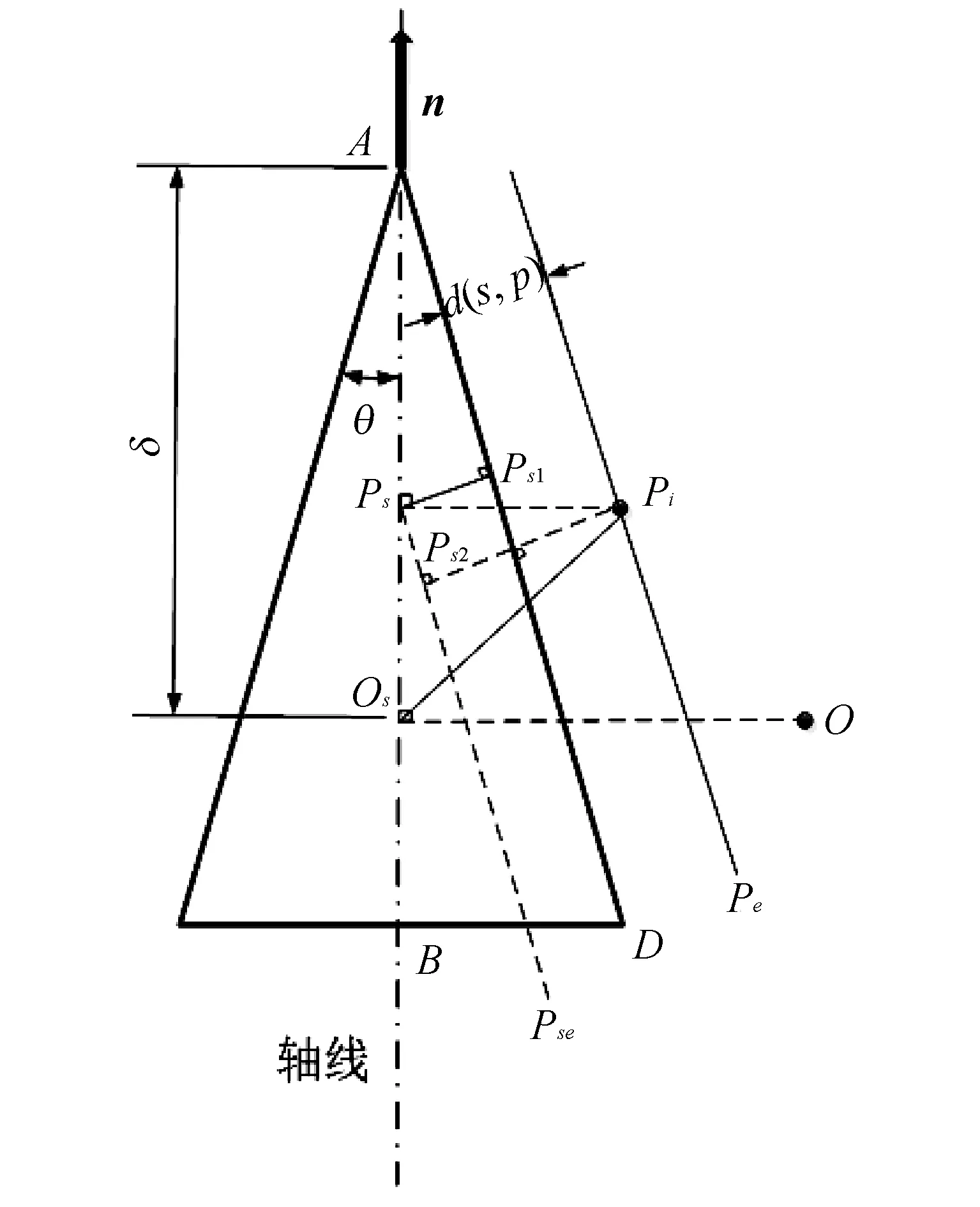
图 1 圆锥面距离函数模型示意图Fig.1 Cone distance function model

图 1 中d(s,p)表示三维数据点Pi到圆锥面的距离，O表示坐标原点，Os表示坐标原点在圆锥面轴线上的投影点， 设Os到圆锥顶点A的距离为δ，Ps为空间点Pi在圆锥面轴线上的投影点，θ为圆锥面的锥顶半角，n为圆锥面单位轴向向量, 其它相关各点的位置关系为

PsPse∥PiPe∥AD,PsPs1⊥AD,P1Ps2⊥AD.

(1)

由图 1 可知

d(s,pi)=|PiPs2|-|P2Ps1|=|PiPs|·cosθ-|APs|·sinθ，

(2)

即

d(s,pi)=(OsP-n〈OsPi,n〉)cosθ-(δ-〈OsPi,n〉)sinθ.

(3)

记:P=PiO,S=OsO则

d(s,pi)=(P-S-n〈P-S,n〉)cosθ-(δ-〈P-S.n〉)sinθ.

(4)

在文献[7]中， Benk″ P得到该距离函数模型带有约束条件的逼近函数表达式

d(s,p)=λp2-〈p,n′〉2+〈p,s′〉+A,

(5)

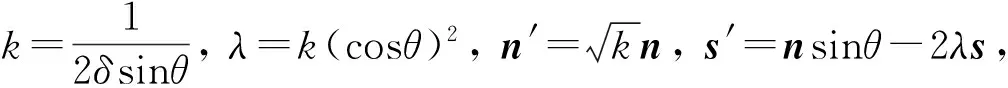
(6)

P=(x2,y2,z2,2xy,2xz,2yz,x,y,z,1)T，

(7)

即知距离函数表达式为:d(s,p)=STP， 则数值迭代优化的目标函数为

(8)

2 圆锥面拟合方法

本文提出基于确定采样策略的圆锥面拟合方法. 由确定采样策略获取的数据点位置信息及数据点的空间几何关系， 可靠准确地估算圆锥面几何参数初值， 再利用非线性最小二乘法求解圆锥面几何参数精确值， 算法稳定可靠.

2.1 采样策略

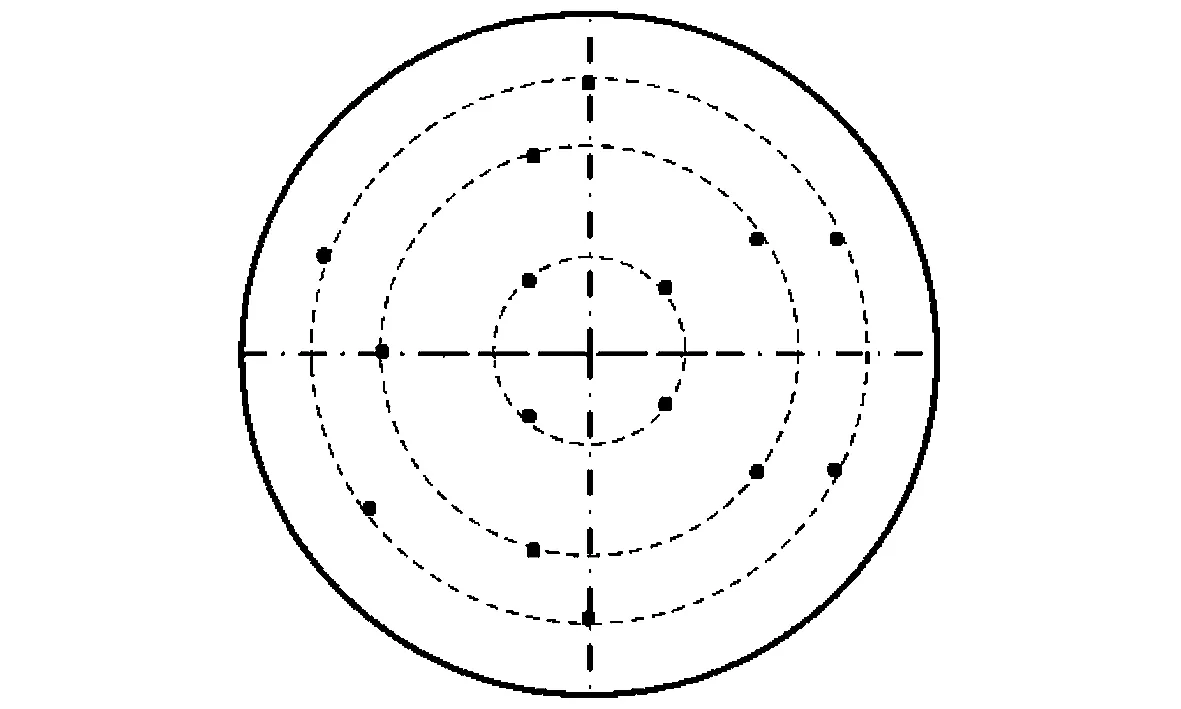
图 2 圆锥面采样示意图Fig.2 Cone sampling diagram

采样策略是影响测量精度、效率的主要因素. 三坐标测量机采样策略内容包含采样点数量及分布. 大卫·弗兰克[8]在三坐标检测策略中推荐圆锥面测量采样点数为12个或15个. 在实际手动测量中常用采样点分布确定方法有： 分层规则均匀采样和随机采样. 文中采用分层规则均匀采样方法确定采样点分布， 保证采样点在采样区域上尽可能均匀分布[9]， 采样点数量选取15个， 具体采样分布如图 2 所示.

图 2 表示圆锥面俯视图， 其中不同直径大小的圆表示圆锥面上垂直于圆锥轴向的空间圆， 空间圆上点表示三坐标测量机采样数据点. 文中确定的采样方案为： 在圆锥面上垂直于圆锥轴向的三个空间圆上采样， 直径最大空间圆上均匀采集6个数据点， 直径最小空间圆上均匀采集4个数据点， 第3个空间圆上均匀采集5个数据点， 采样点数共15个.

在实际手动采样过程中， 数据点分布要求尽可能均匀且分布在与轴向垂直的锥面空间圆上， 这与实验人员操作经验有关系.

2.2 初值计算

依据确定的采样策略， 构建锥面与采样点的空间几何关系， 计算圆锥面几何参数， 即为锥面拟合初值， 锥面与空间圆的几何关系如图 3, 图 4 所示.

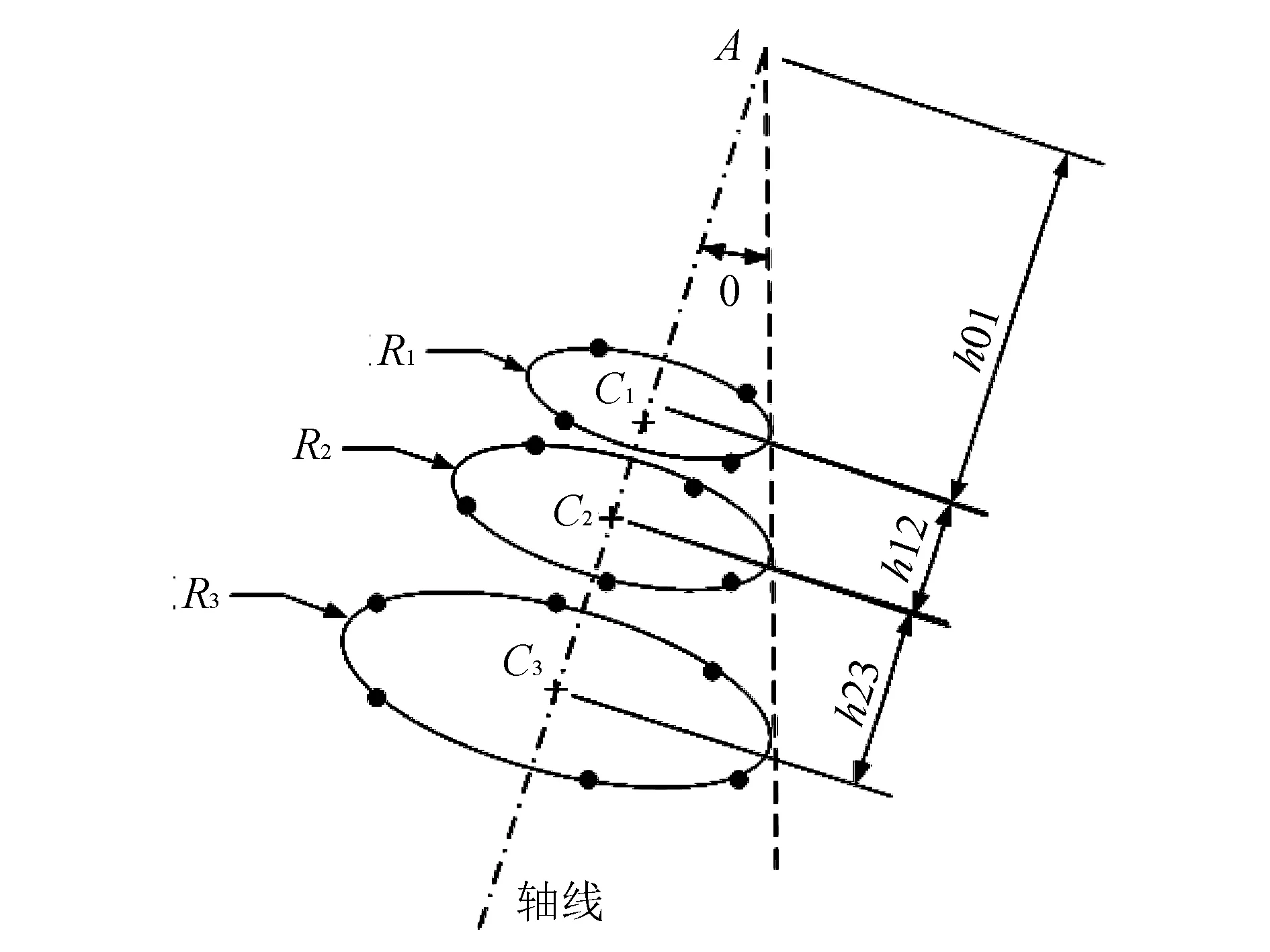
图 3 锥面与采样空间几何关系示意图Fig.3 Spatial relation of Cone and sampling points

图 4 锥面与采样空间圆平面几何关系示意图Fig.4 Flat relation of Cone and sampling circles

本文初值计算方法的步骤为： 由离散数据点坐标， 分别拟合3个空间圆， 计算圆心坐标及半径， 再根据三角几何关系， 计算圆锥面顶点、锥顶半角以及圆锥面轴向向量.

2.2.1 空间圆拟合

在初值计算中， 空间圆拟合过程较为复杂， 空间圆拟合思路是利用坐标变换将空间圆转换为平面圆进行拟合,计算平面圆半径、圆心参数,再利用坐标变换矩阵反求三维圆圆心坐标,最终得到空间圆参数.

空间圆转换为平面圆拟合的具体过程是： 由离散采样数据点， 拟合出空间圆所在平面， 利用平面信息建立新坐标系， 再利用坐标变换将这些数据点坐标转换到新的坐标系下， 即可将空间圆拟合转化为平面圆拟合.

1) 平面拟合. 本文采用分层规则均匀采样方法， 对圆锥面分3层采样， 每层数据点可拟合出空间圆所在平面. 空间平面的一般方程为

Ax+By+Cz+D=0,

(9)

式中：C≠0. 将一般方程转化为

ax+by+c-z=0.

(10)

利用最小二乘思想， 即

(11)

利用函数梯度求解该表达式最小值， 即可求得平面参数a，b，c值.

2) 坐标变换. 在空间圆所在平面上建立新的坐标系， 将拟合该平面的数据点通过坐标转换， 转换至新坐标系下. 坐标变换构造的主要思路是： ① 构造平移矩阵T， 平移原坐标系OXYZ， 使其坐标原点O与新坐标系原点O′重合； ② 构造旋转矩阵R， 利用旋转变换使两坐标系坐标轴重合. 坐标变换的构造方法较多， 在此不予详述. 数据点坐标在新坐标系O′X′Y′Z′中坐标值计算公式为

(x′,y′,z′,1)=(x,y,z,1)·T·R.

(12)

3)平面圆拟合. 新坐标系下空间数据点可视为平面坐标点， 即可以对平面圆进行拟合. 平面圆曲线上数据点满足表达式

f(x,y)=x2+ux+y2+vy+w=0,

(13)

假设测量数据点数为n， 根据误差理论[10]， 由于测量数据点存在误差， 数据点坐标(xi,yi)不满足曲面方程， 将其变形可得单个观测点误差方程为

vi=uxi+vyi+w-(-x2-y2).

(14)

实际测量中， 为提高平面圆拟合精度， 观测点数多于3个点， 形成多余观测， 再进行平差运算， 多观测点误差方程组可整理为

V=AΔa-L,

(15)

式中：

(16)

根据最小二乘平差原理可得

Δa=(ATA)-1ATL.

(17)

计算求得Δa， 即可求得平面圆圆心及半径.

(18)

式中：T为坐标变换中平移矩阵；R为坐标变换中旋转矩阵.

2.2.2 参数计算

圆锥面几何特征参数主要包括: 圆锥轴向向量， 圆锥面顶点坐标及锥顶角. 图 4 表示1/4锥体平面示意图， 其中：R1，R2，R3分别表示3个拟合空间圆半径；C1，C2，C3分别表示3个空间圆的圆心；A表示圆锥面顶点， 直线AB表示圆锥面的轴线；θ表示锥顶半角.

1) 轴向向量. 假设已求得3个空间圆的圆心分别为C1，C2，C3， 空间圆半径分别为：R1，R2，R3， 则圆锥面轴向向量可由3个空间圆圆心C1,C2,C3坐标拟合空间直线AB计算， 空间直线拟合方法在此不予详述.

2) 锥顶点坐标. 锥顶点坐标根据圆心C1，C2，C3在轴线上的投影点之间距离， 利用三角形相似关系， 计算出锥顶点到已求投影点距离,即可求得顶点坐标.

3) 锥顶半角. 锥顶半角θ利用正切计算公式计算:

(19)

2.3 圆锥面拟合算法

建立圆锥面几何距离参数化方程后， 可知距离目标函数是非线性函数， 因此利用Levenberg-Marquardt[11]方法对距离目标函数进行迭代优化计算， 以初值计算求解的圆锥面参数作为迭代优化的初始值.本文基于确定采样策略的圆锥面拟合算法步骤如下：

1) 依据圆锥面距离函数模型,得到锥面距离逼近函数表达式;

2) 利用由确定采样策略获取的三维数据点分别计算空间圆的圆心及半径， 并根据空间圆的几何位置关系计算圆锥面顶点坐标， 锥顶半角及轴向向量;

3) 利用已计算的圆锥面几何参数初值作为迭代初始值， 采用Levenberg-Marquardt方法进行优化计算， 最终得到圆锥面精确参数.

3 实验分析

本节对圆锥面拟合算法进行实验验证. 依据确定的采样策略， 利用三坐标测量机在两个不同轴向位置上对两个不同大小的圆锥体， 分别在1/4圆锥面， 1/2圆锥面， 3/4圆锥面及整个圆锥面区域进行多次采样， 每组实验获取15个采样数据点， 分别利用圆锥面拟合算法及经PTB认证的Rational DMIS软件对圆锥面参数进行计算， 对比计算结果并分析.

本文实验数据较多， 故只列出1/2圆锥面采样和整个圆锥面采样计算结果表格， 如表 1, 表 2 所示， 表中初值计算表示本文初值计算的结果， 算法1数据表示本文算法拟合计算的结果， 算法2数据表示Rational DMIS软件计算的结果， 差值表示两算法拟合结果差值.

表 1 1/2圆锥面采样计算结果

由表 1, 表 2 中数据可知， 本文圆锥面几何参数初值计算结果与圆锥面拟合结果接近， 且本文拟合算法计算结果与Rational DMIS软件计算结果的小数点后两位数基本保持一致， 二者拟合结果的差值很小. 表3是本文算法对圆锥面拟合误差的计算结果， 误差计算方法为： 计算采样点到拟合圆锥面的距离， 最大误差表示采样点到圆锥面的最大距离值， 平均误差表示采样点到圆锥面的平均距离. 由表 3 可知， 在实验中采样区域为1/2圆锥面时， 圆锥面拟合算法拟合最大误差为0.014 104 mm； 采样区域为整个圆锥面时， 拟合最大误差为0.008 603 mm， 综上可知， 本文算法拟合结果准确、精度高.

表 2 整圆锥面采样计算结果

表 3 圆锥面拟合误差计算结果

4 结 论

针对圆锥面拟合初值计算不理想而导致拟合结果不准确的问题， 本文提出基于确定采样策略的圆锥面拟合方法. 该方法利用所有数据点位置信息及其空间几何关系， 可以准确可靠地估算圆锥面几何参数初值， 距离函数优化过程收敛快， 能够快速准确计算目标函数全局最优点. 经实验证明： 本文算法拟合结果精度较高， 解决了拟合初值计算不理想导致拟合不准确甚至失败的问题， 实现了圆锥面的精确拟合， 为三坐标测量软件中标准二次曲面拟合提供了新方法.

[1] 曲学军, 杨亚文, 韩志仁. 基于散乱数据表面法矢的二次曲面拟合[J]. 航空学报, 2007, 28(4)： 1018-1024.

Qu Xuejun, Yang Yawen, Han Zhiren. Quadric surface direct fitting based on normal vectors of random data[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(4)： 1018-1024. (in Chinese)

[2] 李岸, 管爱枝. 基于高斯映射的柱面与锥面点云拟合[J]. 组合机床与自动化加工技术, 2007(8)： 28-32.

Li An, Guan Aizhi. Fitting point cloud to cone and cylinder based on Gaussian image[J]. Combined Machine Tool and Automatic Machining, 2007(8)： 28-32. (in Chinese)

[3] 刘元朋, 赵辉, 陈良骥,等. 基于有向点云数据的二次曲面拟合算法[J]. 机床与液压, 2008(8)： 27-29.

Liu Yuanpeng, Zhao Hui, Chen Liangji, et al. Algorithm of quadric surface fitting from oriented point cloud[J]. Machine Tool & Hydraulics, 2008(8)： 27-29. (in Chinese)

[4] 梁爽, 李明, 杨恢,等. 工业测量中标准二次曲面的一种拟合方法[J]. 组合机床与自动化加工技术, 2012(5)： 49-53.

Liang Shuang, Li Ming, Yang Hui, et al. A method for standard quadric surface fitting in industrial metrology[J]. Combined machine tool and automatic machining, 2012(5)： 49-53. (in Chinese)

[5] Lukács G, Martin R, Marshall D. Faithful least-squares fitting of spheres, cylinders, cones and tori for reliable segmentation[C]. European Conference on Computer Vision. Springer Berlin Heidelberg, 1998： 671-686.

[6] Lee G, Mou J, Shen Y. Sampling strategy design for dimensional measurement of geometric features using coordinate measuring machine[J]. International Journal of Machine Tools & Manufacture, 1997, 37(7)： 917-934.

[7] Benk″ P, Kós G, Várady T, et al. Constrained fitting in reverse engineering[J]. Computer Aided Geometric Design, 2002, 19(3)： 173-205.

[8] 大卫·弗兰克. 三坐标测量指南-测量机检测策略[M]. 诸锡荆, 编译. 2005.

[9] Wong T T, Luk W S, Heng P A. Sampling with Hammersley and Halton points[M]. A. K. Peters, Ltd. 1997.

[10] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉： 武汉大学出版社, 2003.

[11] 陈宝林. 最优化理论与算法[M]. 北京： 清华大学出版社, 2005.