基于人工神经网络的导航卫星钟差预报方法
2018-01-29郭秋,李培
郭 秋, 李 培
(1.晋中职业技术学院,山西 晋中 030600;2.西安邮电大学,西安 710061)
0 引 言
卫星钟差(Satellite Clock Bias,SCB)预报技术是卫星导航定位系统的关键技术之一,对于卫星导航定位具有非常重大的作用。对导航电文发布钟差参数进行处理外推可以得到任何时刻导航卫星的钟差信息,对于参数预报的可靠性和稳定性的提高以及对钟差数据修改上载间隙的优化来说,钟差预报的深入研究具有十分积极的作用。精密单点定位的高精度定位也需要使用钟差预报的结果参与处理,通常的精密单点定位使用的是国际服务组织(Internet GPS Service,IGS)提供的钟差数据,其最终星历卫星钟差精度可达0.1 ns,但是,由于其钟差数据需要经过IGS数据中心处理后得到,存在一定的滞后性,对于单点定位的实时性无法满足。因此需要对SCB高精度预报方法进行深入研究[1]。
文献[2-4]中使用GM(1,1)灰色模型建立钟差预报模型,其优点是使用较少的数据即可建模,并且在短期预测任务中具有较高的精度,但是,用于建立GM(1,1)灰色模型所需的原始数据要求必须为按照指数规律改变,这会对钟差预报产生误差。文献[5-6]中使用最小支持向量机(Least Square Support Vector Machines, LSSVM)建立钟差预报模型,LSSVM算法实际上是算法的误差以及损失函数看作经验损失通过使用等式约束替换不等式约束从而对模型复杂度进行简化,达到提高求解速度的目的。但是,由于LSSVM算法对于惩罚因子以及核函数的选择十分依赖,故使用其建立的钟差预报的模型精度取决于参数的选取,而参数的选取又存在随机性以及不确定性,因此,预测精度和稳定性无法得到保障。
人工神经网络通过数据样本对模型进行训练提高模型泛化能力,已经在时间序列预测领域得到了广泛的应用,但是没有通过优化算法优化的BP神经网络在训练开始时会使用0~1的随机数初始化为将隐含层和输出层的阈值和连接权值,会造成BP神经网络出现陷入局部最小值,降低收敛速率等缺陷。本文使用粒子群优化算法优化BP神经网络的初始阈值和权值,从而建立高精度的钟差预测模型。
1 改进型BP神经网络
1.1 BP神经网络预测模型
本文研究的SCB预报模型属于时间序列预测问题,实际上可以看做是一种求动力系统的逆问题。使用动力系统的状态构造动力系统模型:
F(Xi)=xi+T,T>0
(1)
式中:T为预报的步长。
使用BP神经网络算法是一种典型的、较好的建立时间序列非线性模型,进行逼近所求动力系统模型的方法。
假设非线性动力系统的输入和输出分别为Xi=(xi,xi+τ,…,xi+(m-1)τ)T,和yi=xi+1。本文采用BP神经网络为典型的三层机构,使用其进行SCB预报时,设定BP神经网络输入层维数等于时间序列重构相空间的嵌入维数。设定BP神经网络输入层维数为1,设定BP神经网络隐含层维数为p,则隐含层各个节点的输入表示为:
(2)
式中:θj和wij分别为隐含层各节点阈值和隐含层连接权值,均由BP神经网络训练得到。
隐含层节点输出为:
(3)
j=1,2,…,p
输出层节点输入为:
(4)
输出层节点输出为:
(5)
式中:γ和vj分别是输出层各节点阈值和连接权值,均由BP神经网络训练得到[7]。
1.2 改进型PSO优化算法
假设S维空间中,有一个由n个粒子组成的种群W=(W1,W2,…,Wn)。 在S维空间中,Wi=(wi1,wi2,…,wiS)T表示第i个粒子的位置。通过目标函数求得第i个粒子的位置Wi的适应值。第i个粒子的速度和个体极值表示为:Vi=(Vi1,Vi2,…,ViS)T,Pi=(Pi1,Pi2,…,PiS)T;全局极值表示为:Pg=(Pg1,Pg2,…,PgS)T。
通过个体和全局极值对每一次迭代的粒子速度和位置进行更新方法如下:
(5)
(6)
式中:ω是惯性权重;r1、r2均为随机数,范围在0~1;c1和c2均为加速因子。
本文引入GA算法中的自适应变异因子对部分变量以一定概率进行初始化,避免常规PSO算法出现陷入局部最小值或进入早熟收敛的问题。改进方法如下:
Step1初始化粒子群优化算法的基本参数:种群规模、迭代次数、学习算子和速度位置区间等。
Step2根据卫星钟差预报的要求对BP神经网络的结构进行确定,由随机构成的种群决定BP神经网络初始参数:
Wi=(wi1,wi2,…,wiS)T
(7)
式中:S=RS1+S1S2+S1+S2;R为BP神经网络的输入层维数;S1为隐含层维数;S2为输出层维数。
Step3对由Step 2确定BP神经网络模型进行训练,得到满足精度的输出值。假设粒子个体的适应值为:
(8)
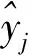
Step4个体和群体的极值的确定由各个粒子的适应值决定,粒子最好的位置确定历史最优位置。
Step5根据每一次迭代的粒子速度和位置进行更新方法、个体和群体极值以及用于确定BP神经网络初始参数的随机构成的种群更新粒子的位置、速度;通过引入GA算法中的自适应变异因子,对部分变量以一定概率进行初始化,避免常规PSO算法出现陷入局部最小值或进入早熟收敛的问题;
Step6迭代次数超过设定最大值后,BP神经网络的结构参数、阈值等使用适应粒子群优化算法确定的最优参数重新确定,从而达到对BP神经网络进行优化的目的[8]。
2 实验分析
下面通过实验研究本文建立的预报模型的性能以及与其他预报模型的差别。选用的实验数据取自IGS网站提供的4颗GPS卫星钟差数据,分别是使用Cs钟的RPN09卫星、PRN10卫星以及使用Rb钟的RPN02卫星、PRN29卫星。其时间间隔为5 min,进行288次连续5 min(即总时长1 d),24次连续1 h(即总时长1 d)以及连续7次1 d(即总时长1周)的预报研究。使用本文研究的方法以及常规PSO-BP神经网络以及常规BP神经网络建立的预报模型进行预报实验,最后将IGS的精密钟差数据作为依据,统计各种算法的均方根误差分析评判各种模型的预报结果[9-10]。
均方根误差计算公式为[11]:
(9)
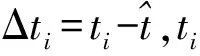
为了提高模型的收敛速度以及降低模式运算量,对实验原始数据进行归一化处理[12]:
(10)
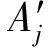
(1) 实验1(288次连续5 min预报)。在进行288次连续5 min(即总时长1 d)时的钟差预报实验主要是对预报模型的超短期预报能力进行测试,得到的预报结果如图1和表1所示。
可以看出,使用本文研究改进BP神经网络方法对288次连续5 min的超短期预报的精度和稳定性均比较好,使用Rb钟的RPN02卫星、PRN29卫星预报精度均能够达到0.6 ns以内。
(2) 实验2(24次连续1 h预报)。在进行24次连续1 min的钟差预报实验得到的预报结果如图2和表2所示。

图1 实验1预报误差
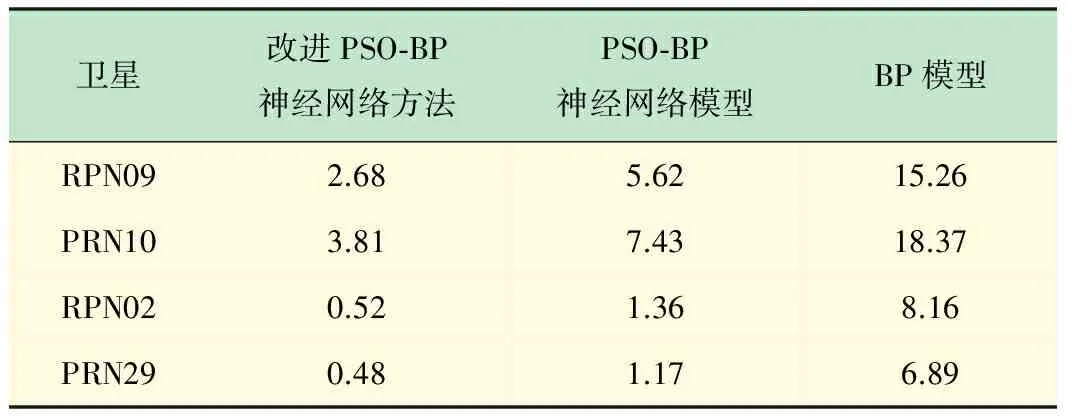

图2 实验2预报误差

可以看出,使用本文改进BP神经网络方法对24次连续1 h的预报中,精度和稳定性均比较好,并且明显优于常规算法建立的模型,使用Rb钟的RPN02卫星、PRN29卫星均方跟误差控制在1 ns之内。
(3) 实验3(7次连续1 d预报)。在进行7次连续1 d的钟差预报实验得到的预报结果如图3和表3所示。

图3 实验3预报误差

通过对3次实验数据进行分析可知,在相同实验条件下,使用改进型人工神经网络建立的预报模型的预报精度要优于常规BP神经网络所建立的模型,说明通过对使用粒子群优化算法对BP神经网络的预测模型进行优化,引入遗传算法中的自适应变异因子来以一定概率初始化部分变量解决常规的粒子群优化算法会出现陷入局部最优解,对于解决BP神经网络容易陷入局部最小值以及训练收敛速率低等问题以及常规PSO算法早熟收敛等问题具有较好的效果。
通过实验数据分析发现,使用Cs钟的RPN09卫星、PRN10卫星的预报精度和预报稳定性要低于使用Rb钟的RPN02卫星、PRN29卫星的预报结果。分析其原因,可能是由于使用Cs钟的GPS卫星的使用年限较长,由于设备老化或者Cs钟的部分物理特性引起的较大的误差。
3 结 论
卫星钟差预报技术是卫星导航定位系统的关键技术之一,对于卫星导航定位具有非常重大的作用。
(1) 本文建立基于BP神经网络的卫星钟差预报模型,使用PSO算法对BP神经网络结构参数和连接权值阈值进行优化;引入自适应变异因子来以一定概率初始化部分变量改进PSO算法。
(2) 通过实验研究本文建立的卫星钟差预报模型性能,结果表明,本文建立的卫星钟差预报模型预报精度和稳定性要优于常规算法建立的模型,说明PSO算法能够解决BP神经网络容易陷入局部最小值以及训练收敛速率低等问题,而改进PSO算法对于避免常规PSO算法早熟收敛等问题具有较好的效果。
(3) 通过实验数据分析发现,使用Cs钟的RPN09卫星、PRN10卫星的预报精度和预报稳定性要低于使用Rb钟的RPN02卫星、PRN29卫星的预报结果。分析其原因,可能是由于使用Cs钟的GPS卫星的使用年限较长,由于设备老化或者Cs钟的部分物理特性引起的较大的误差。
[1] 郭承军,滕云龙.神经网络在卫星钟差短期预报中的应用研究[J].测绘科学,2011,36(4):198-200.
[2] 崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2005,30(5):447-450.
[3] 郑作亚,卢秀山.几种GPS卫星钟差预报方法比较及精度分析[J].山东科技大学(自然科学版),2008,27(4):6-11.
[4] Heo Y J,Cho J,Heo M B. Improving prediction accuracy of GPS satellite clocks with periodic variation behaviour[J].Measurement Science and Technology,2010,21(7):1-8.
[5] 雷 雨,赵丹宁.基于最小二乘支持向量机的钟差预报[J].大地测量与地球动力学,2013,33(2):91-95.
[6] 张清华,隋立芬,王 冰,等.一种利用加窗LSSVM 拟合GPS在轨卫星钟差的算法[J].武汉大学学报(信息科学版),2012,37(9):1032-1035.
[7] 戴文战,娄海川,杨爱萍.非线性系统神经网络预测控制研究进展[J].控制理论与应用,2009,26(5):521-530.
[8] 董超俊,刘智勇.多层混沌神经网络及其在交通量预测中的应用[J].系统仿真学报,2007,19(19):4450-4453.
[9] 郭海荣,杨 生,杨元喜,等.基于卫星双向时间频率传递进行钟差预报的方法研究[J].武汉大学学报(信息科学版),2007,32(1):43-46.
[10] 郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报,2008,49(3):306-320.
[11] 黄观文,杨元喜,张 勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J].测绘学报,2011,40(1):15-21.
[12] 郑作亚,党亚民,卢秀山,等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010,51(1):95-102.
