基于正交试验的弯管热推制成形数值模拟

张向伟， 黄丽丽， 鹿晓阳

(1.山东大学 管理学院，济南 250100；2.山东建筑大学 力学所，济南 250101)

0 引 言

在石油、冶金、化工、锅炉等工业生产装置中，壁厚均匀、小曲率、管壁薄且强度高的管件应用越来越多。如果采用传统的弯管加工方式，因成形过程中弯管管壁凸面受拉力作用而凹面受压力作用，从而容易出现壁厚不均匀的情况。近年来，很多学者对管材成形工艺及工模具结构改进进行了研究和探索[1-9]。薄壁小曲率弯管的成形方法主要有热推制成形法、模压弯曲法、冷顶推弯法和无芯绕弯法等，其中热推制成形法[10-11]是当今各种管材成形工艺中比较有效的成形方法之一。它通过推板将套在芯棒上的管坯推出以得到所需尺寸的弯管，管坯在推至芯棒大头发生扩径弯曲变形时需要进行感应加热。该成形方法理论上能够得到高质量和壁厚均匀的小半径弯管。目前，该工艺已广泛应用于气体、液体或带固体颗粒流体的运输管路及金属结构件中。很多国内外学者和工程技术人员都对该工艺进行了理论分析、实验研究及有限元数值模拟[12-16]。影响弯管成形质量的因素很多，包括：芯棒的几何参数、推板的推制速度、管坯与芯棒之间的摩擦系数、管坯的加热温度等。热推制成形的工艺参数不同，弯管推出后的形状、管壁壁厚及壁厚均匀性等也都不同。本文采用有限元软件MSC. Marc对弯管成形过程进行了数值模拟，设计了正交试验方案，综合分析了加热温度、推制速度、摩擦系数、牛角芯棒的弯曲角度、初始弯曲半径对弯管壁厚和壁厚均匀性的影响规律，获得相对可靠的、优化的工艺参数。对合理设计芯棒几何形状和设定工艺参数具有一定的指导意义。

1 工艺分析及有限元模型建立

本文模拟成形的成品弯管几何尺寸为：公称直径125 mm，外径140 mm，内径128 mm，壁厚6 mm，弯曲半径190 mm的90°弯管，材料为25号钢。采用MSC. Marc 2005有限元软件进行模拟。

1.1 管坯尺寸

管坯的尺寸需要根据弯管的尺寸计算获得，其基本参数可通过表1中的计算公式来确定。根据表1，把相关弯管数据代入公式得管坯外径为103.92 mm，在选择管坯外径时，查《无缝钢管国家标准规格表》发现没有相应规格的管坯，从中选择一个尺寸与之相近的管坯，本文选取外径108 mm、壁厚6 mm的管坯。根据计算管坯长度取425 mm。

表1 管坯参数的确定

注：DW为弯管外径，R为弯管弯曲半径，S为弯管壁厚，θ为弯曲角度(弧度)，DN为弯管公称直径

1.2 芯棒尺寸

芯棒的几何形状设计对弯管成形过程有很大影响，是弯管成形过程中重要的工艺参数之一。经常使用的芯棒依据其轴线形式可分为两类：单半径牛角芯棒和双半径牛角芯棒。这两种牛角芯棒均无法确保弯管生成时弯曲变形和扩径变形一直保持为一个确定的比例数值，甚至连变形的连续光滑性都不能确切保证。为使弯管成形过程始终保持一定的比例关系，牛角芯棒轴线应该是一条连续光滑变曲率的弧线。

基于芯棒轴线的曲率半径和管坯发生变形时的曲率半径在数值上相等的特性，芯棒的轴线可以选用阿基米德螺旋线。芯棒的外形尺寸与阿几米德系数α、弯曲角θ和扩径比K有关。

极坐标阿基米德线公式：

r=αθ

(1)

极坐标曲率公式：

(2)

曲率半径：

(3)

根据弯管轴线弯曲半径和α，将其代入曲率半径公式，可解得θ。在该角度位置，阿基米德线曲率半径可求出，即可确定该位置为芯棒轴线的扩径段与定径段的交界位置。选定扩径段弯曲的角度区间和定径段的成形角度，即可确定扩径弯曲轴线形状。

芯棒主要分为导正段、扩径弯曲变形段及定径段三部分，本文以上述方法为基础进行了牛角芯棒的设计，增加了直锥扩径段，如图1所示。导正段的作用是对管坯进行输送和导正；直锥扩径段目的是对管坯在弯曲扩径前进行准确定位，防止后续管坯导正不良，使管坯在进入扩径弯曲变形阶段发生塑性变形之前越来越紧地抱箍在芯棒上，直锥扩径段尺寸设计要求管坯在该阶段发生的变形为弹性变形；扩径弯曲变形段是管坯发生扩径和弯曲变形的主要部分，此处管坯产生了永久的塑性变形；定径段的作用在于平整工件，使弯管的外径和曲率满足要求。

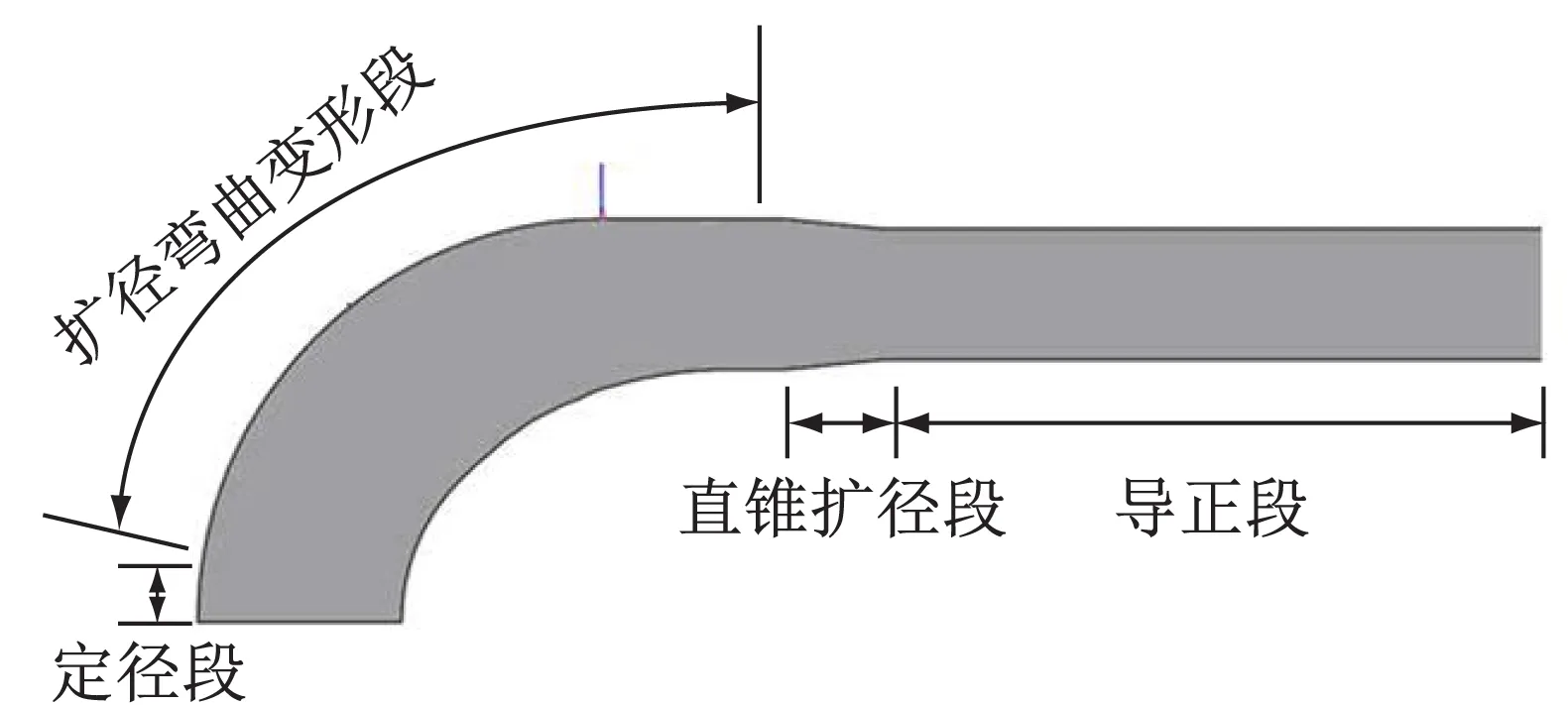
图1 牛角芯棒三维建模

1.3 有限元模型建立及参数设置

芯棒模型由UG软件生成，通过Hypermesh软件进行网格划分，生成16 898个六面体网格单元，然后导入MSC. Marc 2005有限元软件进行模拟。芯棒材料选用热作模具钢4Cr5MoSiV。进行模拟时，在芯棒导正段套3段管坯，每段管坯划分网格数目为1 026。考虑到管坯在推制过程中发生塑性变形和传热，需要进行变形和传热的热力耦合分析，因此选用8节点6面体全积分热力耦合单元(ELEMENT7)；牛角芯棒可视为刚体，采用8节点6面体减缩积分热传导单元(ELEMENT123)。图2所示为弯管推制成形有限元模型，考虑到结构的对称性，选取1/2进行模拟，以减少计算量。

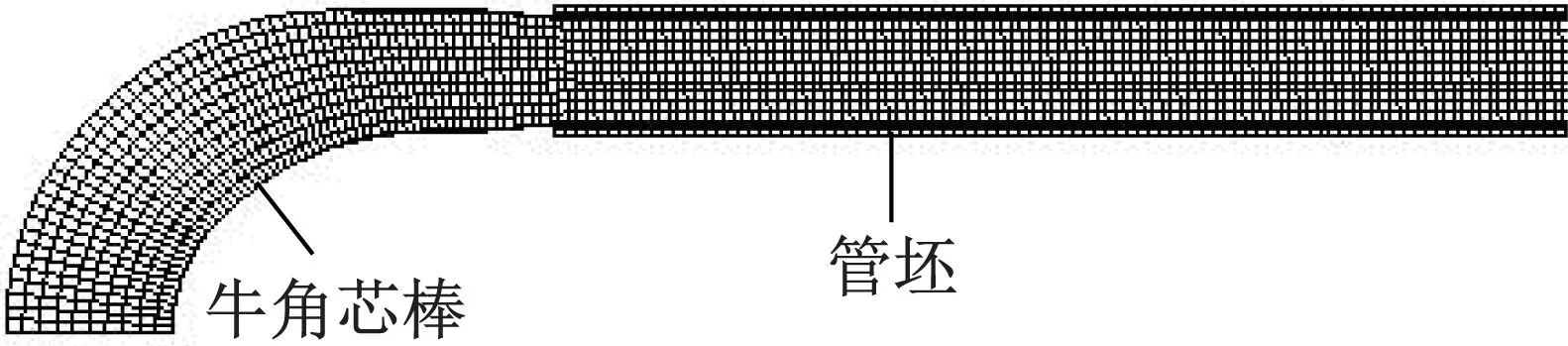
图2 热推弯管有限元模型

热推弯管的工艺参数主要包括加热温度、推制速度、摩擦系数、牛角芯棒的弯曲角度、初始弯曲半径等。模拟试验将针对这些参数进行优化。

参数值根据实际生产经验和以往试验结果选定合理的范围，并尽量均匀取值，以便分析该参数对弯曲成形的影响规律。具体取值为：加热温度分别选取700、750、800和850 ℃；推制速度分别选取2、3、4和5 mm/s；摩擦系数分别选取0.10、0.14、0.18和0.22；芯棒的弯曲角度分别选取35°、40°、45°和50°；初始弯曲半径分别选取1.1、1.4、1.7和2.0。

2 模拟结果及分析

弯管壁厚的变化率和均匀性是弯管成形质量的主要影响因素。弯管热推制成形工艺的特点使得弯管凸边壁厚基本不变，因此弯管凹边壁厚变化率及均匀性对弯管的成形质量有着决定性影响。本文利用模拟试验结果中弯管凹边壁厚均值和方差判定壁厚变化率和均匀性，分析变形规律、优化工艺参数。

2.1 正交表设计

将加热温度A(℃)、推制速度B(mm/s)、摩擦系数C、弯曲角度D(°)和初始弯曲半径E(mm)作为模拟试验因素，5个因素各取4个水平，选用L16(45)正交表(见表2)进行模拟优化设计，共需要16次试验。试验方案如表3所示。

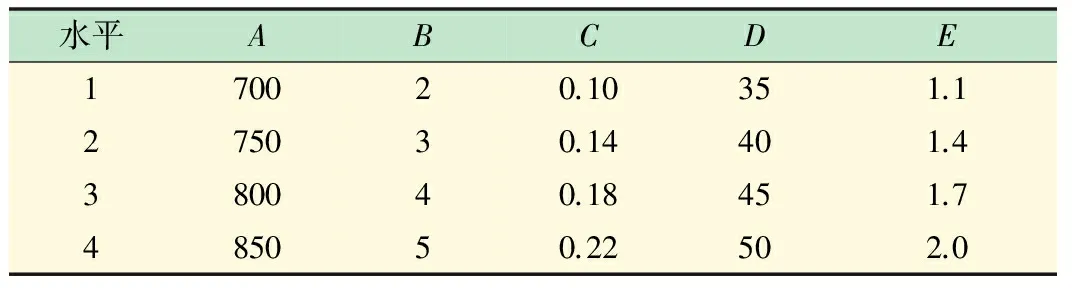
表2 试验因素及水平

2.2 结果分析

采用直观分析的方法对试验结果进行分析，如表4所示。

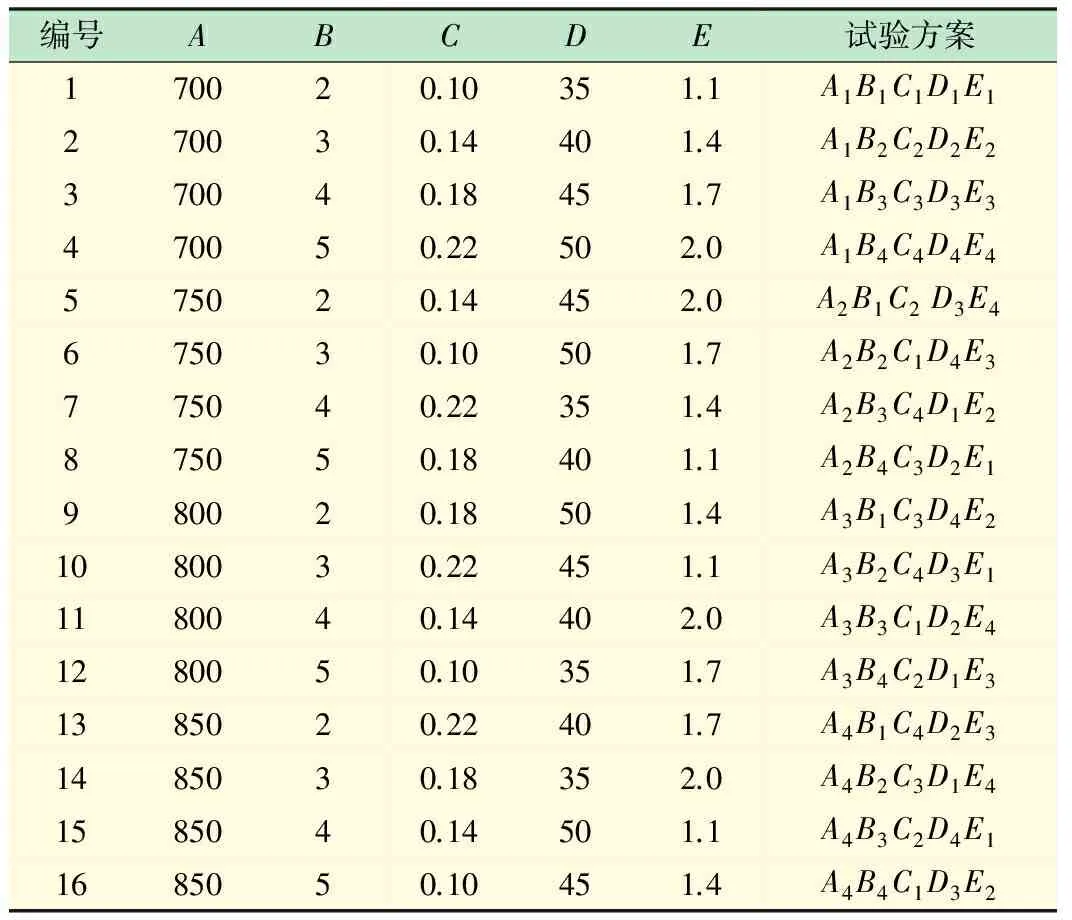
表3 正交试验表

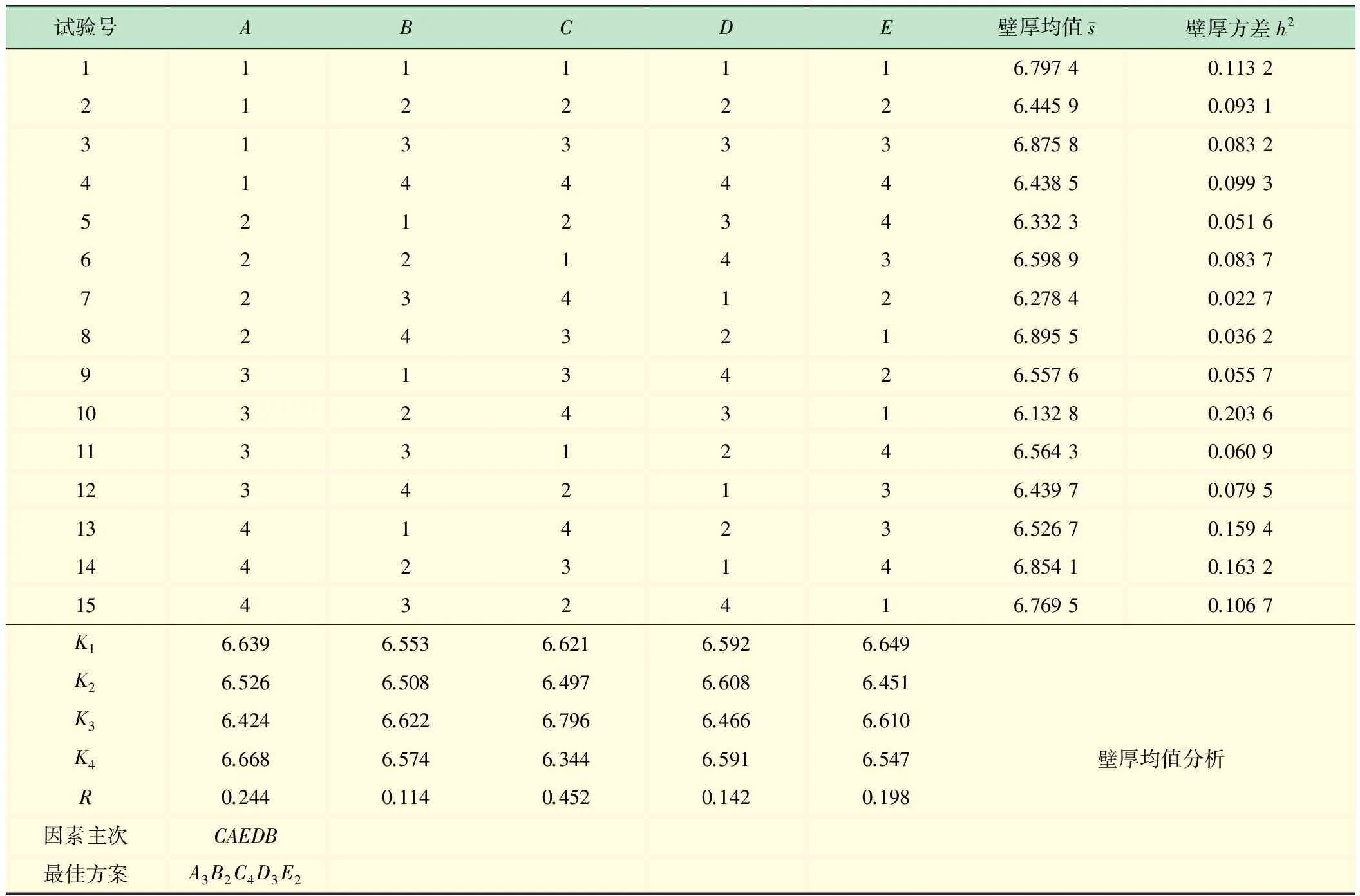
表4 正交试验结果

表4中10号方案(A3B2C4D3E1)壁厚均值为6.132 8 mm，最接近初始壁厚6 mm；7号方案(A2B3C4D1E2)方差最小为0.022 7，表明这组方案壁厚均匀性最好。由表中壁厚均值分析及壁厚方差分析中R值大小可知，各因素对壁厚的影响从大到小依次是CAEDB；各因素对壁厚均匀性的影响从大到小为ABECD。从K值大小可得，壁厚均值的最佳参数组合为A3B2C4D3E2，壁厚均匀性的最佳参数组合为A2B3C2D4E2。

综合平衡分析壁厚变化率和均匀性两个指标，A因素对两个指标的影响显著，3水平对壁厚均匀性的影响优于2水平，2水平对壁厚变化率的影响优于3水平，综合考虑选择2水平；B因素对壁厚变化率的影响大于对壁厚均匀性的影响，选取3水平；C因素对壁厚均匀性的影响大于对壁厚变化率的影响，其中2水平对壁厚变化率的影响优于4水平，4水平对壁厚均匀性的影响优于2水平，综合考虑选取3水平；D因素同样对壁厚均匀性的影响大于对壁厚变化率的影响，选取3水平；E因素对两个指标的影响相同，选取2水平。因此最终确定最优方案为A2B3C3D3E2。

由于该试验获得的最佳方案不在已做过的16组试验中，因此需要追加试验进行最佳方案的模拟，所得壁厚均值和方差分别为6.085 8 mm和0.010 9，追加试验较优。

3 结 语

对弯管的热推制成形工艺进行了分析，采用Marc有限元分析软件对弯管成形进行了模拟，获得了弯管成形过程的金属流动情况。利用正交试验法，分析得到了各参数对弯管凹边壁厚均值和均匀性的影响程度。

利用正交试验法，以凹边壁厚变化率最小及均匀性良好为目标，得到了等壁厚弯管成形的最优参数为A2B3C3D3E2，即加热温度A为750 ℃，推制速度B为4 mm/s，摩擦系数C为0.18，芯棒的弯曲角度D为45°，初始弯曲半径E为1.4。

[1] 张保军, 杨 合, 郭良刚, 等．基于虚拟正交试验的Incone1690合金大口径壁厚管挤压工艺仿真[J]．稀有金属材料与工程, 2013, 42(3):487-493.

[2] 万 鹏. 数控无芯弯管的成形技术研究[D]. 南京:江苏大学, 2014.

[3] 牟 菊, 门向南, 陈清根, 等. 基于ABAQUS有限元模拟铝合金小弯曲半径的内压推弯成形[J]. 热加工工艺, 2015(13):109-112.

[4] 陈清根, 徐雪峰, 王高潮,等. 铝合金弯头冷推弯成形影响因素研究及工艺参数优化[J]. 塑性工程学报, 2015, 22(6):40-46.

[5] 刘劲松, 张兴华, 刘 海, 等．薄壁钢管内胀推弯成形数值模拟及实验研究[J]．锻压技术, 2012, 37(2): 63-66．

[6] Li H, Yang H. A study on multi-defect constrained bendability of thin-walled tube NC bending underdifferent clearance[J]. Chinese Journal of Aeronautics, 2011; 24(1): 102-112.

[7] Zhang Z, Yang H, Li H,etal. Thermo-mechanical coupled 3D-FE modeling of heat rotary draw bending for large-diameter thin-walled CP-Ti tube[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(9):1187-1203.

[8] Poor H Z, Menghari H G, Sousa R J A D,etal. A novel approach in manufacturing two-stepped tubes using a multi-stage die in tube hydroforming process[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(11): 2343-2350.

[9] Ge Y L, Li X X, Lang L H,etal. Optimized design of tube hydroforming loading path using multi-objective differential evolution[J]. International Journal of Advanced Manufacturing Technology, 2017, 88(1-4):837-846.

[10] 鹿晓阳, 史宝军, 徐秉业,等. 牛角芯棒热推弯管成形过程力学原理及分析求解方法[J]. 塑性工程学报, 1999(3):31-36.

[11] 李鸿翔. 不锈钢管材推弯成形有限元模拟及实验研究[D]. 大连:大连理工大学, 2015.

[12] 张尧武, 曾卫东, 戴 毅,等. 基于虚拟正交试验的热推弯管工艺参数优化设计[J]. 塑性工程学报, 2009, 16(6):91-95.

[13] 李林涛, 曾卫东, 殷京瓯,等. 中频感应加热纯钛弯管成形过程中的有限元模拟[J]. 锻压技术, 2006, 31(6):131-134.

[14] 裴文娇. 核级厚壁管热推弯成形有限元模拟及试验研究[D]. 南京:南京航空航天大学, 2015.

[15] Lu X Y, Zhou Q T, Huang L L,etal. Numerical simulation and parameter optimization of hot pushing elbow pipe bending pProcess[J]. Applied Mechanics & Materials, 2013, 432(3):92-97.

[16] Huang Lili, Lu Xiaoyang. Technology analysis of hot pushing pipe bending and horn mandrel design[J]. Advances in Engineering Research. 2015, 26, 842-845.