基于离散余弦变换过完备字典的机织物纹理稀疏表征

吴 莹， 汪 军,2， 周 建

(1. 东华大学 纺织学院, 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620；3. 江南大学 纺织服装学院， 江苏 无锡 214122)

目前，市场上机织物面料储存仍以实物样品为主，如何有效地运用计算机实现纺织面料的存储、分类和织物纹理表征是数字化纺织研究的难点之一，而织物纹理表征与分析是其核心问题。此外，纺织品纹理分析可促进纺织品产品质量指标评价的客观化和定量化，进而为纺织品质量检测自动化的实现提供基础条件。高效地表征织物纹理不但可应用在自动瑕疵检测织物纹理分类、褶皱自动评级等领域，还可应用在遥控操作机器、电子商务等其他领域[1]。

与人工分析织物纹理相比，计算机视觉技术不仅可有效地提高检测准确率，而且可更客观地评定纺织品的外观和内在质量。织物纹理表面分析主要涉及到2个方面[2]：1)客观测定表面纹理的几何或统计特征，如织物褶皱的自动等级评定[3]、织物密度的自动检测、组织自动识别[4]等；2)分析纺织品表面纹理的特征缺陷，如基于字典学习织物瑕疵点自动检测[5-7]和基于其他方法的织物瑕疵点自动检测[8-10]。毛兆华等[11]用非负字典学习的方法对机织物瑕疵区进行检测，该算法不仅能够有效地近似重构织物纹理图像[12]，而且在保证误检率较小的同时获得90%的检出率。稀疏表征是采用极少的原子以简洁、稀疏的形式来展现信号的内部结构。机织物纹理种类繁多且风格复杂多变，本文将重点研究如何采用较少的投入来表征机织物表面纹理，而这种想法恰好与稀疏表征不谋而合。与传统方法相比，图像稀疏分解更接近于图像表示方法，更贴近图像的本质特征，因此，稀疏表征方法的研究有着极其重要而深远的理论意义和广泛的实用价值。字典学习的稀疏冗余表达在图像压缩处理等各种应用中展示了优越性，如在纹理分类、静态图像和视频的去噪等应用中都取得了比较好的结果。Zhou Jian等[13]用稀疏字典对机织物纹理瑕疵进行检测，并证明该方法在自适应织物纹理上具有显著的优势。

虽然字典学习的稀疏表征为机织物纹理图像的分析和表征提供了新的有效工具，但针对机织物纹理表征方面的研究较少。现有的研究大都着重于纹理表征的应用，如织物瑕疵检测、织物组织结构自动识别等，因此，机织物纹理表征作为基础研究，寻找合适的算法对其表征是非常必要的。学习字典或者初始字典为随机字典得到的表征效果不稳定，为固定表征效果，本文探讨采用离散余弦变换(DCT)过完备字典对机织物纹理进行稀疏表征。

1 信号的稀疏表征

任意给定信号矩阵X=[x1,x2,…,xn]，xi∈Rm，信号的稀疏表征在l2范数近似条件下构造的优化函数为

(1)

式中：T为正整数，控制稀疏程度；‖αi‖0为式中非零项的个数。

式(1)是一个解的正确性可被“容易检查”(NP-hard)问题，目前比较经典的近似优化技术有匹配追踪算法(matching pursuit algorithm)、最小二乘法正交匹配追踪算法(LS-OMP)、分步正交匹配追踪算法(Stage-wise OMP)[14]以及弱匹配追踪[15]算法、基追踪算法(Basis Pursuit, BP)[16]等。因为正交匹配追踪(OMP)算法简洁有效，所以本文选择OMP来获取稀疏系数。

2 DCT过完备字典的构造

式(1)中D、α都是未知数，首先选择字典后才能进而获得稀疏表征模型， 因此，字典的选择至关重要。图1示出常见的字典类型。包括基于传统数学模型的字典(DCT字典)和基于训练的自适应学习字典(K-SVD字典)；根据数学变换得到的解析字典，如曲线波(Curvelet)[17]、离散余弦变换(DCT)[18]等；由设计字典训练算法得到的自适应学习字典，经典的算法有最优化方向法(MOD)[19]、K奇异值分解法(K-SVD)[20]。

DCT 作为初始字典；K-SVD 是斜纹迭代5次训练得到的；非稀疏是最小二乘法交替迭代100 次学习得到的。图1 预先定义的字典和学习字典Fig.1 Predefined dictionary and learned dictionary. (a) DCT dictionary; (b) K-SVD dictionary; (c) Non-sparsity learned dictionary

预先设计的字典没有更新字典的步骤，只需要进行求解稀疏系数矩阵，因此，方便快捷，但也限制了其应用；训练的自适应字典尽管需要设计字典训练算法，相对较复杂，但其自适应性更强，可更好地稀疏表征图像信号。为得到稳定的机织物纹理表征效果，本文采用预先选择的过完备字典。机织物是在织机上由经纬纱按一定规律交织而成的织物，具有很强的周期性。DCT字典对周期信号有着良好的分解能力，可有效地提高处理效率，故本文选择DCT过完备字典对机织物纹理进行表征。

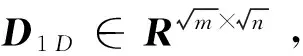
(2)

3 机织物纹理图像的稀疏表征

机织物纹理稀疏表征的公式为

(3)

式中ε为残差。

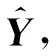
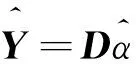
(4)

3.1 稀疏表征结果的评价指标

关于重构图像的客观评价指标，目前还没有统一的方法，而单一的评价指标都有一定的不足，因此，本文选择均方根误差和峰值信噪比作为评价指标。

3.1.1均方根误差

均方根误差是用来衡量观测值同真实值之间的偏差，其定义为

(5)

式中：M为Y的维数；N为Y中样本的个数。

3.1.2峰值信噪比

峰值信噪比可对不同图像的近似质量进行有效地客观评定，其定义为

(6)

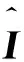
4 稀疏表征参数的优选

由式(4)可知，在重构机织物纹理之前，需要确定合适的稀疏程度、残差ε以及字典个数k。残差值ε以均方根误差为量化指标进行控制。

4.1 稀疏度

稀疏度是控制重构系数基数的关键指标，不同稀疏度下重构机织物纹理图像的结果见图2。由图可知，随稀疏度的增大，均方根误差逐渐减小，在T=10后，均方根误差的下降速率逐渐变小，但程序运行所需的时间逐渐增多。在重构机织物纹理图像时，在保证重构质量的前提下，尽可能找到最稀疏的系数矩阵。不同稀疏度T下重构的样本图像如图3所示。当T<9时，图像的左侧会有一部分阴影，这是因为稀疏度太小导致系数不足以重构样本图像；T=9时重构图像和原图像非常相似，所需的运行时间也较为合理。因此，本文所选择的稀疏度为10。

图2 稀疏度T对重构机织物纹理的影响Fig.2 Impact of sparsity on characterization of woven fabric texture. (a) XRMSE of reconstructed image with different T; (b) Computing time of reconstruction image with different T

图3 原图和不同稀疏度T的重构效果图Fig.3 Original image and reconstruction result. (a) Original image; (b)T=1; (c)T=3; (d)T=5; (e)T=7; (f)T=9

4.2 子窗口大小

在机织物纹理图像的稀疏表征过程中，由于采用的是过完备字典，如果直接对整幅织物图像进行处理，计算量会非常大，如一幅256像素×256像素的织物样本图像，字典冗余度为3，字典中的原子个数达2.0×105，其内积计算对于一般计算机来说非常困难[22]，因此，本文将图像分成相互重叠的图像块，不仅可减小每个原子大小，还能降低字典的规模。

由机织物的结构参数可知，其在经纬向都存在明显的周期性，因此，合适的子窗口更有利于近似重构机织物纹理图像。在机织物稀疏表征过程中，字典个数k为256，稀疏度为10。以原料为20 tex×2的棉双股线，密度为300根/10 cm的菱形斜纹为例，不同子窗口下重构图像的峰值信噪比如表1所示，其近似的样本图像见图4。由表1可知，子窗口增大，峰值信噪比逐渐减小，重构近似样本的视觉效果没有显著差异，而到子窗口为16像素×16像素时，重构近似样本的可视化效果明显变差，近似的图像也不完整。这是因为子窗口大于图像本身，图像块会包含阴影部分，所以重构的效果很差。稀疏表征中采用的都是过完备字典，即字典的列大于行。如果窗口大小大于或等于16像素×16像素，为非过完备字典，字典没有冗余性，重构效果会变差(见图4)。子窗口2像素×2像素、4像素×4像素虽然峰值信噪比值较8像素×8像素的大，但是由于尺寸太小而包含太少的纹理循环，反而不利于机织物纹理的近似重构，所以其视觉效果不如8像素×8像素，因此，本文选择的子窗口大小为8像素×8像素。

表1 不同子窗口大小的峰值信噪比值Tab.1 XPSNR value of different size patches

图4 不同子窗口的重构效果Fig.4 Illustration of reconstruction results of original image (a) and with size patches 2 pixel×2 pixel (b), 4 pixel×4 pixel (c), 8 pixel×8 pixel (d), 16 pixel×16 pixel (e) and 32 pixel×32 pixel (f)

4.3 字典个数

虽然本文采用过完备字典重构机织物纹理图像，但字典个数k还需进一步探讨，以便选择出更适合于机织物纹理的字典尺寸。为更简明地描述字典个数k对重构效果的影响，这里引入字典冗余度r的概念:任意字典D∈RM×Q，则r=Q/M。

字典个数k和冗余度r、子窗口大小w的关系为

k=r×w×w

图像块选取的是8像素×8像素，冗余度为r=[1，2，3，4，5，6]，则相对应的字典个数k=[64，128，192，256，320，384]。保证其他条件一致的情况下，不同字典个数k的近似效果见图5。

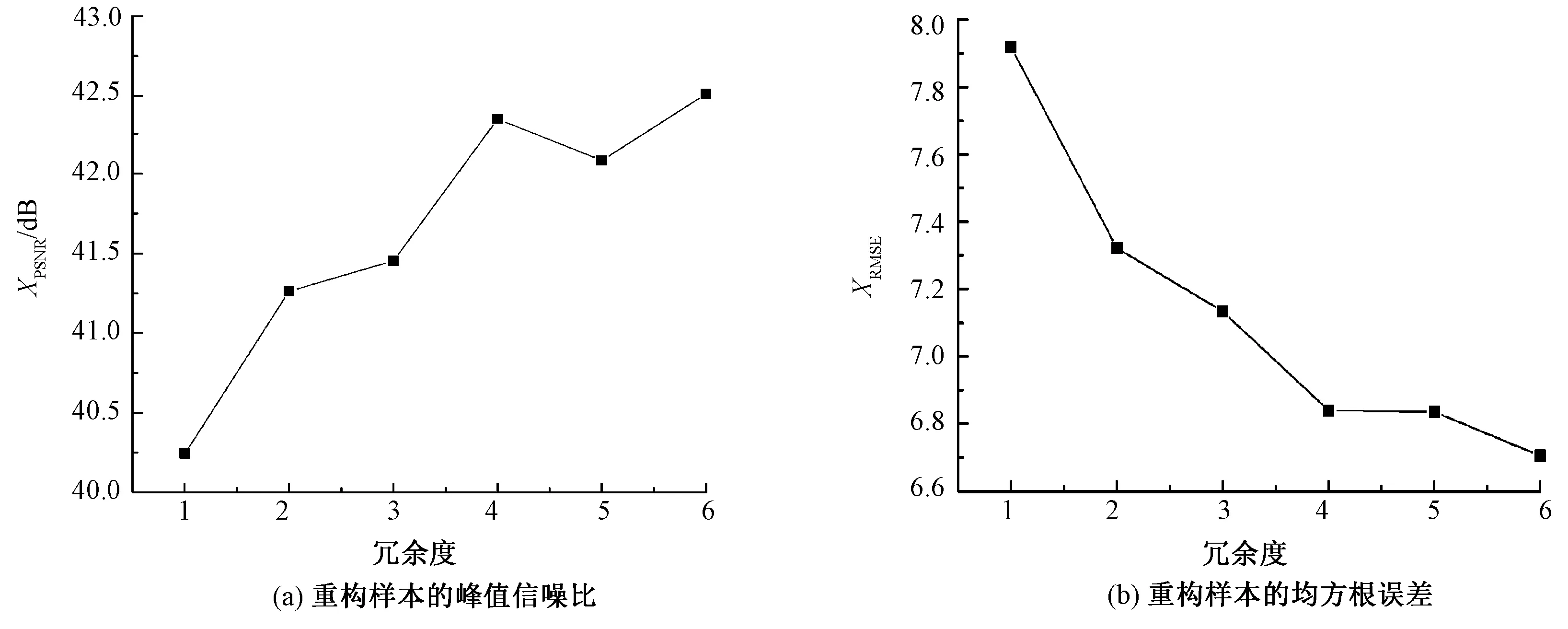
图5 不同冗余度下的重构效果Fig.5 Approximate results with different redundancies. (a) XPSNR value of reconstructed samples; (b) XRMSE of reconstructed samples

当r<5时，r值增大，峰值信噪比逐渐增大，均方根误差逐渐减小；当r>5时，r值增大，峰值信噪比都是先减小后增大。这是由于冗余度过大造成过度拟合，因此，本文选择冗余度为4的字典，最终字典个数k为256。

5 试验结果与讨论

5.1 样本的选取

本文试验中采用了8个样本图像，具体规格参数见表2。本文采用的样本皆为8位灰度图像，尺寸为256像素×256像素。首先，选取8像素×8像素的子窗口，在每个织物样本图像上按水平和垂直方向滑动，共62 001个子样本，所有的子样本按列展开得到64×62 001的样本数据集。

表2 织物样本规格参数Tab.2 Specification parameters of woven fabrics

5.2 机织物纹理图像的稀疏表征

在稀疏度T=10，子窗口为8像素×8像素，字典个数k=256时，根据式(4)对机织物纹理进行稀疏表示，本文算法重构得到的样本如图6所示。

图6 稀疏表征重构的机织物纹理图像Fig.6 Reconstructed woven fabric images using sparse representation. (a)-(h) Original images of sample 1-8; (i)-(p) Reconstructed images of sample 1-8

由图6可知，不论是三原组织，还是蜂巢等复杂的织物组织，重构样本的视觉效果都与原样本没有明显差异，因此，本文算法可较好地重构机织物纹理。除方平组织外，样本5～8的重构效果较样本1～3差。试验样本的XPSNR值都大于38 dB，XRMSE值都小于11，其中样本1(斜纹)的重构效果最好。可见，不同材质及组织结构样的表征效果具有较显著的差异。织物纹理图像的稀疏指标测试结果见表3。

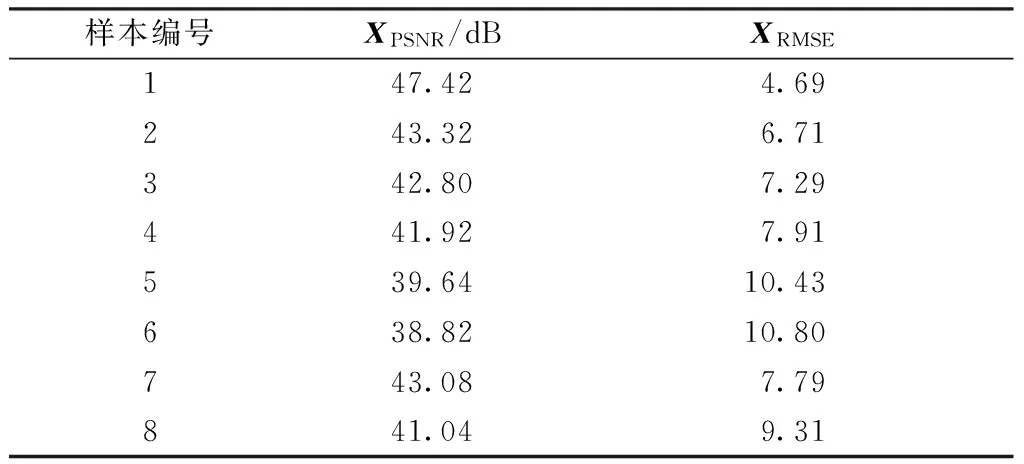
表3 试验样本的测试结果Tab.3 Test results of fabric samples

5.3 稀疏表征与其他方法的比较

为验证算法的有效性将本文算法与其他3种方法进行比较，如主成分分析 (PCA)[23]、非稀疏字典学习算法[23]、K-SVD学习字典法[22]。K-SVD和非稀疏表征的学习字典的初始字典为DCT字典，而学习字典中可看到斜纹样本的特征(见图1)，这是学习字典的优势。试验结果如表4所示，K-SVD学习字典重构的织物样本效果最好，本文算法的重构效果仅次于K-SVD学习字典，但是明显优于非稀疏字典学习算法。因为K-SVD 算法中包括字典更新和稀疏表征系数更新2个阶段，所以其计算量要远大于本文算法。此外，该算法得到的表征结果不稳定。作为经典数据图像处理方法的PCA，其重构机织物样本图像的峰值信噪比值约比本文算法小4.0 dB。与本文算法相比，非稀疏学习字典和PCA的重构织物纹理效果稍微差些。

表4各种方法的峰值信噪比值比较

Tab.4 XPSRN comparison of different algorithms dB

6 结 论

本文提出了一种机织物图像重构的研究方法，即DCT过完备字典稀疏表征，着重探讨了稀疏度T、子窗口个数和字典个数对机织物图像重构效果的影响，并通过构造量化指标均方根误差和峰值信噪比来进一步优选参数。试验结果表明，当稀疏度T=10，子窗口大小为8像素×8像素，字典个数k为256，即冗余度为4时，机织物能得到稳定的近似重构效果图像。与PCA、非稀疏表征、K-SVD算法相比，本文算法在保证结果稳定的条件下，重构效果仅次于K-SVD。本文算法不仅方便快捷，而且还可得到稳定的织物纹理表征结果，为纺织品的在线检测提供正常机织物纹理的模板。

在以后的研究中，将进一步探究机织物纹理表征的影响因素，如组织结构、经纬密、纱线线密度等对近似表征的影响，也将进一步优化算法进而对机织物纹理进行有效分类。

[1] WANG Xin, GEORGANAS N D, PETRIU E M. Fabric texture analysis using computer vision techniques [J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(1): 44-56.

[2] 贡玉南, 华建兴, 黄秀宝. 纺织品表面纹理的图像分析方法[J]. 中国纺织大学学报, 1998, 24(2): 111-114.

GONG Yunan, HUA Jianxing, HUANG Xiubao. On the image analysis of the textile textures [J]. Journal of China Textile University, 1998, 24(2): 111-114.

[3] LIU Chenxia, FU Yaqin, WU Niying. Novel testing equipment for fabric wrinkle resistance simulating actual wear[J]. Textile Research Journal, 2014, 84(10): 1059-1069.

[4] LACHKAR A, BENSLIMANE R, D′ORAZIO L, et al. Textile woven fabric recognition using Fourier image analysis techniques: part II: texture analysis for crossed-states detection[J]. Journal of the Textile Institute, 2005, 96(3): 179-183.

[5] LI Chunlei, YANG Ruimin, LIU Zhoufeng, et al. Fabric defect detection via learned dictionary-based visual saliency[J]. International Journal of Clothing Science and Technology, 2016, 28(4): 530-542.

[6] QU Tao, ZOU Lian, ZHANG Qinglin, et al. Defect detection on the fabric with complex texture via dual-scale over-complete dictionary[J]. Journal of the Textile Institute, 2015, 107(6): 1-14.

[7] NGAN H Y T, PANG G K H, YUNG N H C. Review article: automated fabric defect detection: a review[J]. Image & Vision Computing, 2011, 29(7): 442-458.

[8] LI Pengfei, ZHANG Huanhuan, JING Junfeng, et al. Fabric defect detection based on multi-scale wavelet transform and Gaussian mixture model method [J]. Journal of the Textile Institute, 2014, 106(6): 1-6.

[9] 王钢, 周建, 汪军, 等. 采用奇异值分解的机织物瑕疵检测算法[J]. 纺织学报, 2014, 35(7): 61-66.

WANG Gang, ZHOU Jian, WANG Jun, et al. Woven fabric defect detection using singular value decomposition [J]. Journal of Textile Research, 2014, 35(7): 61-66.

[10] 田承泰, 步红刚, 汪军, 等. 基于时间序列分形特征的织物瑕疵检测[J]. 纺织学报, 2010, 31(5): 44-47.

TIAN Chengtai, BU Honggang, WANG Jun, et al. Fabric defect detection based on fractal feature of time series [J]. Journal of Textile Research, 2010, 31(5): 44-47.

[11] 毛兆华, 汪军, 周建, 等. 应用非负字典学习的机织物瑕疵检测算法[J]. 纺织学报, 2016, 37(3): 144-149.

MAO Zhaohua, WANG Jun, ZHOU Jian, et al. Woven fabric defect detection based non-negativedictionary learning[J]. Journal of Textile Research, 2016, 37(3): 144-149.

[12] 毛兆华, 万贤福, 汪军, 等. 基于字典学习的机织物图像重构[J]. 东华大学学报(自然科学版), 2016, 42(1): 35-39.

MAO Zhaohua, WAN Xianfu, WANG Jun, et al. Woven fabric image reconstruction based on dictionary learning [J]. Journal of Donghua University (Natural Science Edition), 2016, 42(1): 35-39.

[13] ZHOU Jian, SEMENOVICH D, SOWYMA A, et al. Sparse dictionary reconstruction for textile defect detection[C]// International Conference on Machine Learning and Applications. Washington: IEEE, 2013:21-26.

[14] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094-1121.

[15] TEMLYAKOV V N. Weak greedy algorithms[J]. Advances in Computational Mathematics, 2000, 12(2): 213-227.

[16] CHEN S S B, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit [J]. Siam Journal on Scientific Computing, 1998, 20(1): 33-61.

[17] CANDES E J, DONOHO D L. Continuous curvelet transform： I： resolution of the wavefront set [J]. Applied and Computational Harmonic Analysis, 2005, 19(2): 162-197.

[18] WANG Yunhe, SHI Miaojing, YOU Shan, et al. DCT inspired feature transform for image retrieval and reconstruction[J]. IEEE Transactions on Image Processing, 2016, 25(9): 4406-4420.

[19] ENGAN K, AASE So, HUSOY J H. Frame based signal compression using method of optimal direc-tions (MOD) [C] //IEEE International Symposium on Circuits and Systems. Orlando: IEEE, 1999: 1-4.

[20] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[21] ELAD M. Sparse and Redundant Representations[M]. New York: Springer, 2010:227-244.

[22] 蔡红. 基于稀疏表征的SAR图像压缩方法研究 [J]. 计算机工程与应用, 2012, 48(24): 177-181.

CAI Hong. SAR image compression based on sparse representation[J]. Computer Engineering and Applications, 2012， 48(24)：177-181．

[23] 周建. 基于字典学习的机织物瑕疵自动检测研究[D]. 上海：东华大学, 2014:29-36.

ZHOU Jian. Automated woven fabric defect detection using dictionary learning[D]. Shanghai: Donghua University, 2014: 29-36.