高速电脑绣花机结构优化设计

周俊荣， 江 励

(五邑大学 机电工程学院， 广东 江门 529020)

电脑绣花机是一种电脑控制系统与绣花机械的有机结合，可刺绣出各种美丽图案的机电一体化纺织设备。我国绣花机生产是从20世纪90年代开始逐步发展起来的，到2016年底已占据市场总额的85%左右；但产品大多是参照国外机型而研制生产的普通平绣机器，产品精度、质量以及可绣制的花色品种与国外先进机型相比还有较大差距，特别是图案具有很强立体感的链目毛巾绣，基本上被国外公司所垄断[1]。对于高端特种绣花机的关健零部件，国外厂商均设有专利保护，很难进行模仿制造。随着社会的进步和劳动力成本的提高，要求刺绣设备速度更快，精度更高，噪声更低。目前国内链目毛巾绣电脑绣花机的主轴速度只能达650 r/min左右，刺绣效率难以满足当前市场的需求。当主轴速度提高到1 000 r/min以上时，会明显出现断线率上升、噪声和振动变大等问题，甚至会发生机构卡死等事故[2]。实践证明原机械结构已不能适应高速机的发展。

本文在分析传统绣花机机头机械结构和运动特性的基础上，对其机头结构进行了改进设计，将槽型凸轮机构改为带预紧弹簧的盘形凸轮机构，并对凸轮轮廓曲线进行优化设计。然后在ADAMS环境下，对优化前后针杆机构的受力情况进行仿真分析，并在主轴转速超过1 000 r/min的情况下，对绣花机横梁进行了振动测试实验以验证机构优化后的效果。优化后的机构在绣花机高速刺绣的情况下，仍能保持较低的振动噪声和断线率。

1 现有电脑绣花机结构分析

机头部分是电脑绣花机最为核心的执行机构。研究发现，电脑绣花机的振动和噪声主要来源于机头。

分析电脑绣花机机头机械结构不难发现，其主要包括4部分，如图1所示。1)针杆机构。其主要作用是携带线料在布料间上下穿梭，以实现绣花工作，实现其上下往复运动的机械结构是凸轮连杆机构。2)机壳。其主要作用是固定和连接绣花机机头。3)护嘴机构。该机构的执行元件包裹住针杆，通过其与针杆相互配合的上下往复运动绣出具有立体质感的花色品种，实现其上下往复运动的机械结构也是凸轮连杆机构。4)压脚机构。其主要作用是当针杆机构进行布料刺绣时压住布料，使布料不能随绣针一起向上移动，当针杆完成一次布料刺绣时则向上抬起，以便布料可以前后移动进行花样刺绣，实现其上下往复运动的机械结构仍是凸轮连杆机构。

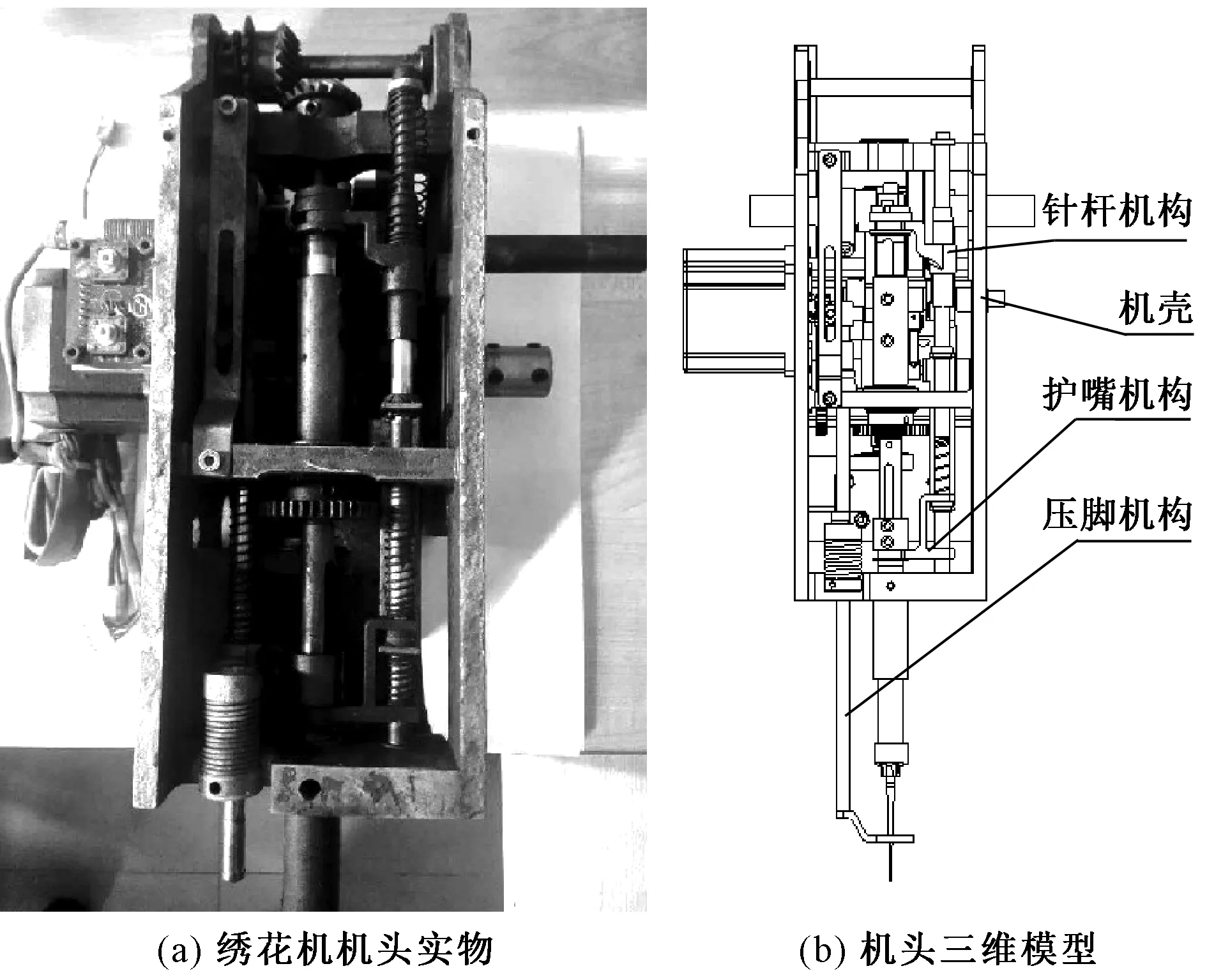
图1 电脑绣花机机头Fig.1 Head of computerized embroidery machine. (a) Object of embroidery machine head; (b) 3-D Model of head

从以上分析可知，电脑绣花机机头主要作用是按照一定的时序实现针杆机构、护嘴机构和压脚机构的上下运动[3-5]，而实现这些运动的主要机械结构均为凸轮连杆机构。本文选择其中最为典型的针杆机构进行详细的分析和研究，如图2所示。

图2 针杆机构Fig.2 Needle bar mechanism. (a) Model of needle bar mechanism; (b) Sketch of needle-bar mechanism

如图2所示，该机构的运动原理是：槽型凸轮1转动带动滚子2在其槽内运动并推动连杆3绕B点旋转运动，而滑块5则在连杆3的驱动下上下运动并带动针杆6上下往复运动。设驱动连杆3与y轴的夹角为θ1，滑块连杆4与y轴的夹角为θ2，OB与y轴的夹角为θ，由几何关系可得出针杆上下运动位移的表达式

Y=LBCcosθ1+LCDcosθ2+c

(1)

当凸轮转动时，∠OBA会跟随凸轮的转动发生变化，若用δ来表述凸轮转动量，则ψ(δ)可描述凸轮输入使得∠OBA的变化，则：

θ1=θ-(∠ABC-ψ(δ))

(2)

(3)

式中：a为凸轮中心O到B点距离在x轴上的投影；b为凸轮中心O到D点距离在x轴上的投影；c为滚子中心A到B点距离在y轴上约投影。将式(2)、(3)代入式(1)中便可得到凸轮输入与针杆运动的关系。将该绣花机机头尺寸参数代入式(1)中，最终可得凸轮转角与针杆位移曲线关系。

将该曲线对时间求2次导数，可得凸轮转速为1 000 r/min时，凸轮转角与针杆加速度曲线关系图，如图3所示。

图3 针杆机构加速度曲线Fig.3 Acceleration curve of needle bar mechanism

通过上文对电脑绣花机机头机械结构和运动规律的研究发现，现有机器存在以下问题：

1)机械结构设计不合理。以针杆机构为例，实现其上下运动的主要机构为槽型凸轮连杆机构，滚子被限制在槽内以便和凸轮充分接触。该机械结构在理论上虽然没有问题，但对加工和装配精度要求很高。当制造能力达不到要求时容易导致凸轮和滚子间有接触间隙，而该间隙则是高速时产生过大噪声和振动的主要原因之一。此外，即使制造精度足够高，凸轮与滚子在长期运转过程中也会产生磨损，使得接触间隙逐渐变大，从而影响绣花机的高速性能[6-7]。

2)凸轮机构运动曲线设计不合理。从图3可看到，该凸轮机构在凸轮转角为90°和270°附近时针杆运动加速度出现明显的突变。这种突变会带来柔性冲击力，在低速时此冲击力的大小和频率还不高，但在高速时，该冲击力的大小和频率会变得很大，成为另一个产生过大噪声和振动的主要原因。

2 电脑绣花机优化设计

针对现有电脑绣花机存在的问题，在进行优化设计时应满足如下要求：1)优化凸轮连杆机械结构，解决凸轮与滚子之间的间隙问题，并能够自动调节由于磨损而产生的间隙。2)优化凸轮轮廓曲线，解决运动机构加速度不连续的问题，减小柔性冲击力所产生的噪声和振动的影响。

2.1 机械结构优化

根据上述第1点要求，首先需要改变凸轮机构的传动方式。采用带预紧弹簧的盘形凸轮机构是一个很好的选择，如图4所示。一方面该方案大大降低了制造和装配精度的要求；另一方面弹簧所提供的预紧力可方便地自动调节磨损所带来的接触间隙。

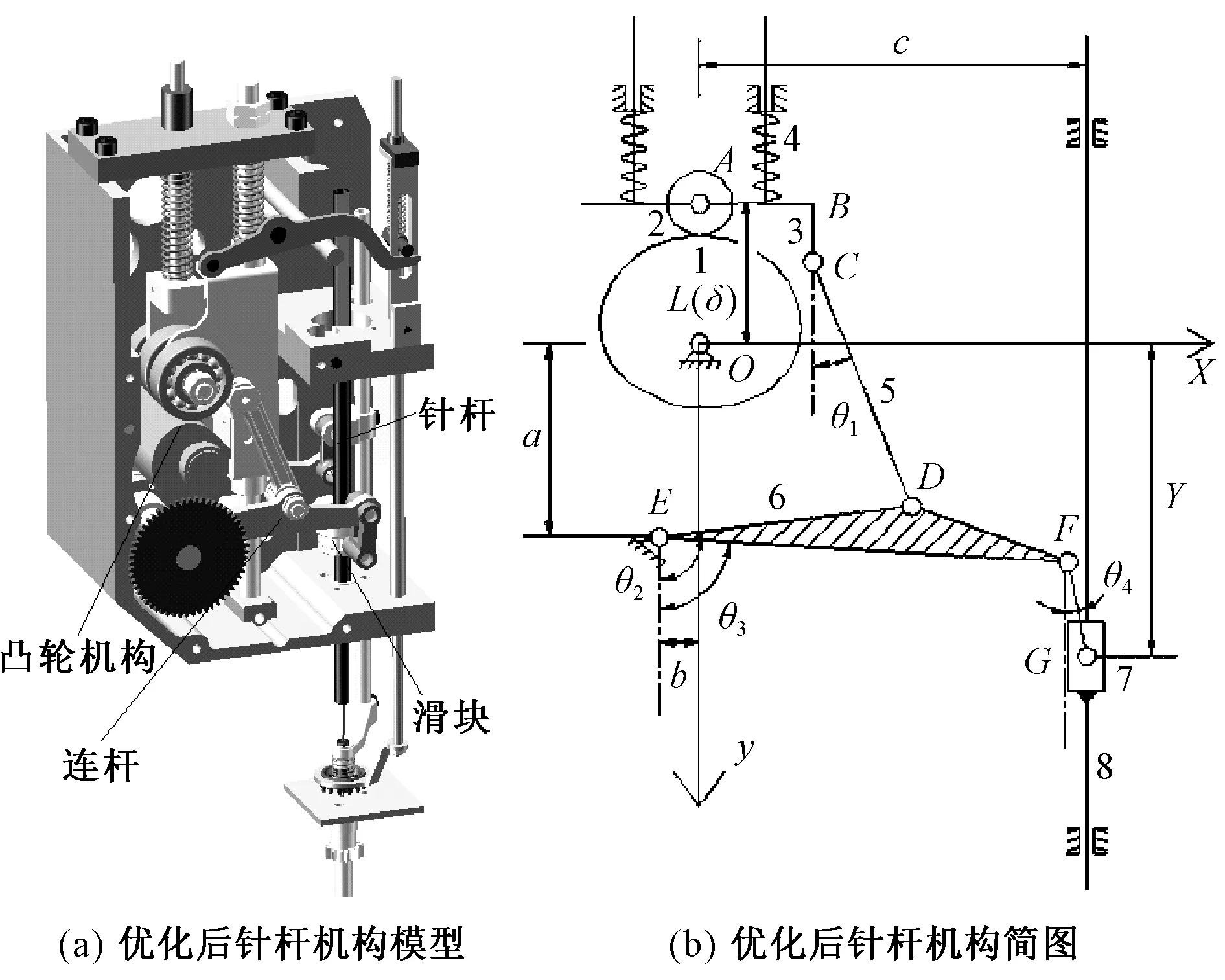
图4 优化后的针杆机构Fig.4 Optimized needle bar mechanism. (a) Model of optimized needle bar; (b) Sketch of optimized needle bar mechanism

在该优化方案中，由凸轮1转动推动滚子2和推杆3上下运动，再由推杆3、驱动连杆5和摆动连杆6组成的连杆结构推动滑块7和固定在其上的针杆8上下运动。弹簧4则保证滚子2始终压紧在凸轮1上。其中，连杆结构形成了一个增力杠杆，可以减小驱动力矩，并调节针杆上下运动的行程。设驱动连杆5与y轴夹角为θ1，摆动连杆上边界DE与y轴夹角为θ2，摆动连杆下边界EF与y轴夹角为θ3，连杆FG与y轴夹角为θ4，则由几何关系可得出针杆上下运动位移的表达式

Y=a-LEFcosθ3+LFGcosθ4

(4)

当凸轮转动时，中心点O到推杆3的距离会随之发生变化，若用L(δ)来描述凸轮转动使得该距离的变化，则由几何关系可得方程组

(5)

式中：a为凸轮中心O到E点的距离在y轴的投影；b为凸轮中心O到E点的距离在x轴的投影；c为凸轮中心O到针杆的距离在x轴的投影；d为凸轮中心O到C点的距离在x轴的投影。将方程组(5)结果代入到式(4)便可得到凸轮输入与针杆运动的关系。

2.2 凸轮轮廓曲线优化

凸轮的轮廓曲线直接决定了绣花机机头的运动规律；而凸轮的轮廓设计过程通常是在其他零件结构尺寸确定的情况下，将运动件的运动规律代入到机械结构中进行反求，故凸轮的轮廓曲线设计实质上就是运动件运动规律的设计。本文将通过对针杆运动规律的分析来优化针杆凸轮的轮廓曲线。

一般来说，运动件的运动规律包括等速运动规律、等加速度运动规律、简谐运动规律、样条曲线运动规律、摆线运动规律等。在进行运动规律设计时主要关注以下几个关键参数：

1)最大无量纲速度VM。VM值越小，凸轮的基圆半径也就越小，从而可以实现减小凸轮机构尺寸的目的；因此，在设计时，应优先选择VM值较小的运动规律。

2)最大无量纲加速度AM。加速度越大，惯性力也就越大，惯性力过大会加剧构件的磨损，因此，在中、高速凸轮机构中，通常优先选择AM较小的运动规律。

3)最大无量纲跃度JM。减小跃度的幅值有利于机构的工作平稳性，因此，应控制JM值不超过某一个值，并且值越小越好。

4)最大无量纲转矩TM。在高速凸轮机构中，惯性负荷决定了施加在凸轮上的输入扭矩大小，因此，为了减小凸轮轴的转矩、降低电动机的功率，应选用TM值较小的从动件运动规律。

对于绣花机来说，它是一个典型的高速低载系统，高次样条曲线运动规律和摆线运动规律都具备跃度连续、无冲击的特点，符合系统的要求，但考虑到这2种运动规律在高速运动时速度波动较大，本文选用摆线运动和等加速运动的组合运动规律，采用5段衔接：1) 摆线加速段，δ∈[0,φ/8]；2) 等加速度段，δ∈[φ/8,3φ/8]；3) 摆线运动段，δ∈[3φ/8,5φ/8]；4) 等减速段，δ∈[5φ/8,7φ/8]；5) 摆线减速段，δ∈[7φ/8,φ]。式中φ为凸轮推杆行程的相位角。它能够在速度没有太大波动的前提下保证加速段连续，如式(6)～(10)所示。

1)摆线加速段：

(6)

2)等加速段：

(7)

3)摆线运动段：

(8)

4)等减速段：

(9)

5)摆线减速段：

(10)

式中：A,V,S分别描述针杆运动的加速度、速度和位置；Ca,C1,C2，…，C11均为待求参数。若用h代表针杆的行程，则该组合运动规律的边界条件可总结为：δ=0时，A=0，V=0，S=0；δ=φ时，A=0，V=0，S=h；中间衔接点，A,V,S连续。

将上述边界条件代入到式(6)～(10)中，便可求解Ca,C1,C2，…，C11，最终得出针杆的运动规律曲线。图5示出优化前后的针杆运动曲线。

图5 针杆运动曲线优化前后对比图Fig.5 Comparison of motion curves of needle rod before and after optimization. (a) Displacement curves; b) Velocity curves; (c) Acceleration curves

对比图5中的曲线可看到：优化后的针杆运动速度曲线更加圆滑，最大无量纲速度VM显著减小；而加速度曲线更为平缓，最大无量纲加速度AM显著减小；在凸轮转角为90°和270°附近时，加速度曲线连续，最大无量纲跃度JM幅值大为减小。这些均反映出优化后针杆运动规律得到了改善。

3 仿真及实验验证

为对电脑绣花机优化改进后的效果进行验证，本文分别进行了在ADAMS环境下的动力学仿真和真实工况下的振动测试实验。

3.1 ADAMS环境下的动力学仿真验证

老款绣花机在高速情况下产生过大振动和噪声的主要原因可以归结为机构内部在高速运转时产生过大的冲击力。通过ADAMS环境下的仿真，可以在高速运转工况下对优化前和优化后的内部受力情况进行对比仿真，从而对电脑绣花机的优化效果进行验证。图6示出针杆机构受力分析虚拟样机。

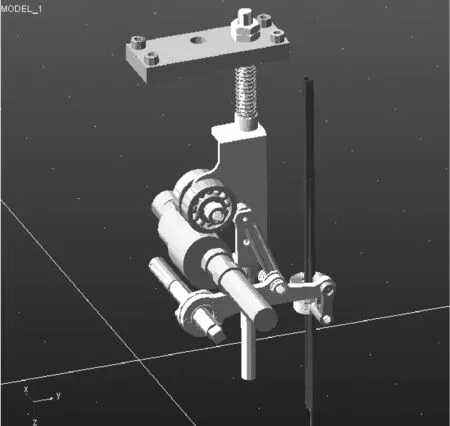
图6 针杆机构虚拟样机Fig.6 Virtual prototype of needle rod mechanism

对于高速运动的机械设备来说，易产生冲击振动的地方无疑是发生在具有相对运动关系且相互作用力不断变化的零件之间。对针杆机构而言，驱动连杆5和摆动连杆6(对照图4)的铰接处是需要关注的地方。本文在凸轮高速(1 000 r/min)转动时，对优化前和优化后此处的受力情况进行仿真对比，如图7所示。

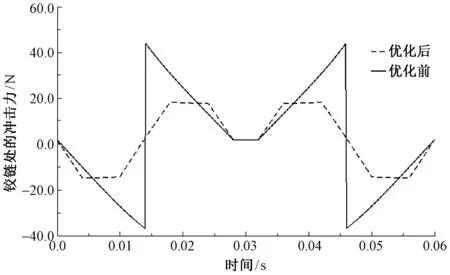
图7 优化前后铰链的受力对比图Fig.7 Comparison force of hinge before and after optimization

从图7可看出，通过对凸轮轮廓曲线的优化，该处铰链在竖直方向受力情况有了明显的改善。首先其受力的最大值由43.8 N减小到18.1 N；其次，原本在0.012 s和0.047 s时会出现由43.8 N到-37.5 N的柔性冲击，经过优化后，此处的冲击力也大为减少。

3.2 高速绣花机振动测试验证

由于电脑绣花机的机头、线架都布置在横梁上，因此，横梁的振动大小可直接反映出绣花机机头的振动大小。相关的计算和实验结果也表明，电脑绣花机横梁的振动是影响其断线率和工作效率的最主要的原因，而且由于绣花机横梁处的振动更加便于测量；故本文对优化后绣花机的振动测试集中于其横梁处[8-10]。实验过程如图8所示。

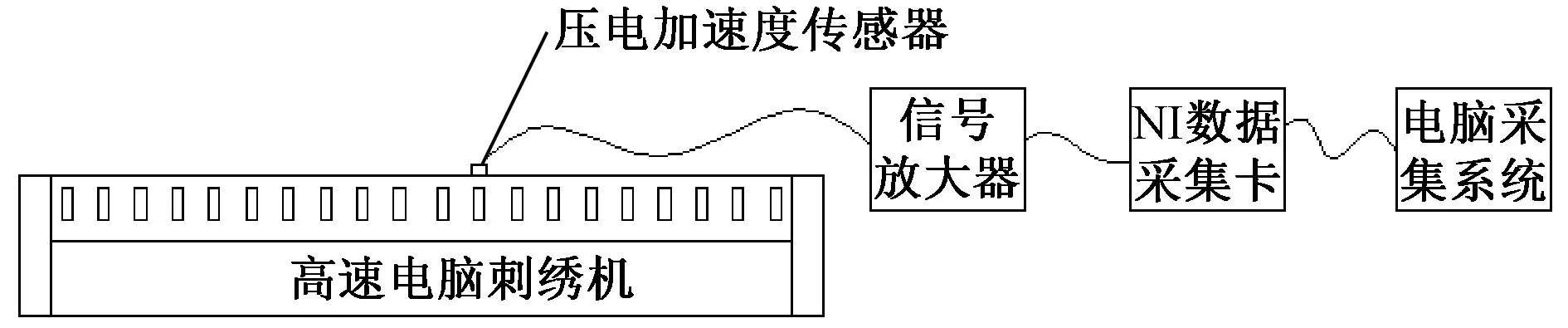
图8 振动测试方法示意图Fig.8 Schematic diagram of vibration test method

测试过程中，将主轴转速分别开到1 100 r/min和1 200 r/min，测试点布置在20头绣花机横梁的中间位置，采样频率设置为2 500 Hz，采样时间为2 s。最终，得到的测试数据如图9所示。将实验测得的波形数据输入到MatLab中，并进行2次积分，便可得到横梁的振动位移曲线，如图10所示。

图9 振动测试实验数据Fig.9 Experimental data of vibration test

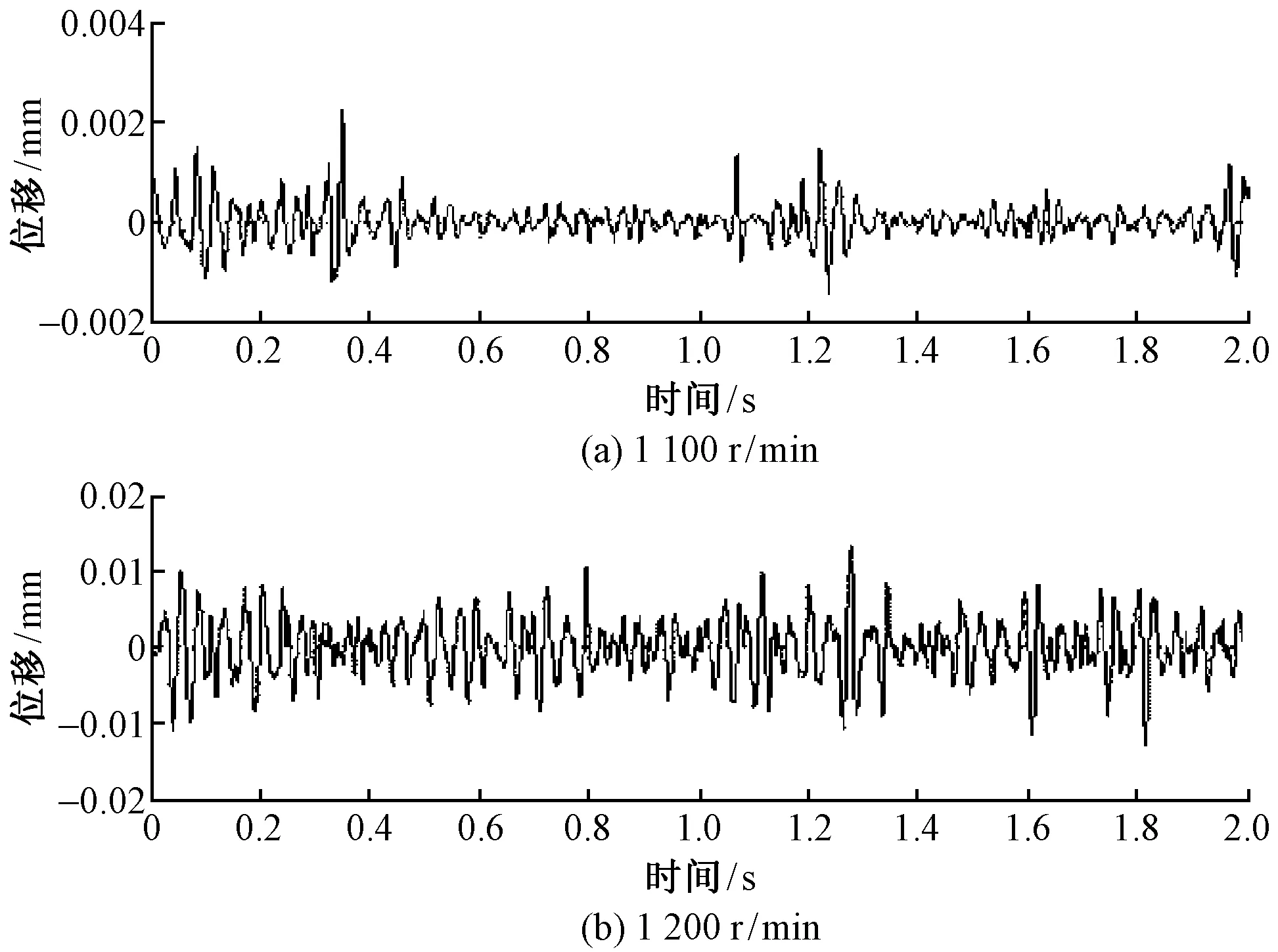
图10 横梁振动位移曲线Fig.10 Displacement curves of crossbeam vibration

由图10可看出，横梁在主轴转速分别为1 100、1 200 r/min时，其振动最大位移分别为0.0 022、0.013 mm。该振动范围远远小于绣花机的误差允许范围[-0.1 mm，0.1 mm]，证明了优化后的高速绣花机机头在噪声振动的降低上有着良好的效果。同时，将该改进产品应用于生产，在实际使用过程中，断线率小于1次/2万针，噪声小于85 dB，得到了用户的好评。

4 结 论

针对传统绣花机在主轴转速超过1 000 r/min时会产生过大的振动噪声，并且断线率过高的问题，对高速电脑绣花机机头结构部分进行分析和优化。首先通过对传统绣花机机头机械结构和运动特性的分析，认为导致振动和断线率提高的主要原因是凸轮传动结构不合理。然后设计了一种带预紧弹簧的盘形凸轮机构取代了原有的槽型凸轮机构，并对凸轮轮廓曲线进行了优化。最后分别通过在ADAMS环境下对针杆机构的受力仿真和绣花机横梁在高转速下的振动测试实验对优化的效果进行了验证。结果表明，相较于传统方案，优化后的方案在高速情况下机器可保证较低的振动噪声和断线率。

[1] 罗本华．电脑刺绣技术发展趋势展望[EB/OL]．[2013-04-17] ．https://club.1688.com/article/31413614.htm.

LUO Benhua. Development trend of computer embroidery technology [EB/OL]. [2013-04-17] ．https://club.1688.com/article/31413614.htm.

[2] 秦荣.电脑绣花机断线问题的研究[J]. 纺织机械，2010(2)：41-44.

QIN Rong. Study on disconnection problem of computerized embroidery machine[J]. Textile Machinery，2010(2)：41-44.

[3] 周俊荣,郑为东.电脑绣花机刺布机构与挑线机构运动分析[J]. 上海工程技术大学学报，2008，22(2):136-140.

ZHOU Junrong, ZHENG Weidong. Kinematic analysis of tread taking up and needle driving mechanism in computerized embroidery machine[J]. Journal of Shanghai University of Engineering Science，2008,22(2):136-128.

[4] 刘良宝,王新,赵罘, 等.电脑刺绣机刺布机构结构优化设计[J].纺织学报，2011，32(5):126-129.

LIU Liangbao，WANG Xin，ZHAO Fu，et al. Optimized design of needle bar mechanism of computer embroidery machine[J]. Journal of Textile Research,2011，32(5):126-129.

[5] 潘丹丹.某电脑绣花机动力学仿真分析与减振研究[D].南京：南京理工大学,2012：36-51.

PAN Dandan. Dynamic simulation analysis and vibration reduction of a computerized embroidery machine[D]. Nanjing：Nanjing University of Science and Technology,2012：36-51.

[6] 林建龙，罗智文，张力． 电脑刺绣机针杆机构位置精度分析[J]．纺织学报，2010，31(7): 131- 134.

LIN Jianlong， LUO Zhiwen， ZHANG Li． Position accuracy analysis on needle bar mechanism of computerized embroidery machine[J]． Journal of Textile Research，2010，31 (7): 131-134.

[7] 郭惠昕. 刺绣机含间隙针杆机构的运动稳健性分析与优化设计[J].纺织学报，2011，32(11):131-136.

GUO Huixin. Position robust analysis and design optimization of needle bar mechanism with joint clearance of automatic embroidery machine[J]. Journal of Textile Research,2011，32(11):131-136.

[8] ZHOU Junrong. The optimization of the beam of high-speed computerized embroidery machine [J]. Applied Mechanics and Materials, 2013, 470:381-384.

[9] 崔卫国，周俊荣，李志飞. 高速绣花机不同工况振动特性研究[J]. 机床与液压，2014，42(17)：102-108.

CUI Weiguo，ZHOU Junrong，LI Zhifei. Research of vibration characteristics of high-speed embroidery machine under different conditions[J]. Machine Tool & Hydraulics, 2014，42(17)：102-108.

[10] 白皛,赵罘,林建龙, 等. 刺绣机横梁的模态分析及优化设计[J].机械设计与研究，2010，26(1):111-116.

BAI Qiao, ZHAO Fu, LIN Jianlong, et al. Modal analysis and optimal design for the beam the embroi-dery [J]. Machine Design and Research, 2010，26(1):111-116.