应用三层热防护服热传递改进模型的皮肤烧伤度预测
2018-01-29卢琳珍徐定华徐映红
卢琳珍, 徐定华,2, 徐映红
(1. 浙江理工大学 理学院, 浙江 杭州 310018; 2. 上海财经大学 数学学院, 上海 200433)
在消防及金属炼钢等行业中,工作人员常处于高温高辐射的环境。这种危险的环境通常被划分为普通、危险、紧急3种状态[1]。紧急状态通常发生在闪火环境下,当热流密度达到20~209.34 kW/m2[1],这时火场人员的耐受时间仅仅有几秒钟,存在致命的危险。在闪火条件下,最常见的热流密度是80 kW/m2[2],由热对流和辐射组成,在火场人员逃离火灾现场仍能持续数秒(少于5 s)。由于暴露在火灾中的时间和强度的不同,一般将烧伤的程度分为1~3级。本文研究将采用由Stoll等[3]和Takata[4]提出的烧伤判断标准来预测达到各级烧伤程度的时间。
近年来,关于热防护服传递模型的研究已成为热点问题。现有的模型根据热防护服是采用单层还是多层材料,分为单层和多层模型。单层模型中热防护服只有外壳,国内外研究者主要研究其外部火焰的辐射热量、织物的物理学性质以及织物与皮肤之间的空气层厚度等因素对防护服热性能的影响。Gibson[5]提出了高温条件下单层多孔介质传热传质模型,但该模型忽略了热辐射的影响。为了改进模型,Torvi[2]提出了在考虑不同辐射条件下的热防护服外壳材料的热传递模型。由于空气层的厚度对热防护服特性有一定的影响,Torvi等[6]在考虑空气层厚度对防护服热性能影响的基础上,建立了用于计算冷却过程中内部传热和皮肤受伤时间的模型。在圆柱坐标系下,朱方龙[7]研究了不同曲面下的热传递过程。基于ASTM D 4108的实验装置,Sawcyn等[8]发展了预测防护服和空气层的热传递模型。Chitrphiromsri等[9]在Gibson和Torvi模型的基础上提出了多孔介质的防护服内部热湿耦合模型。之后Song[10]将其与实验数据比对,验证了该模型的可靠性。Ghazy等[11]基于热防护服-空气层-皮肤系统建立了运动中的单层织物热传递模型。
在单层模型的基础上,许多学者研究了热防护服热湿传递多层模型。Mell等[12]提出了包含热传导和热辐射的多层面料层与层之间的传热模型。由于相变材料对热防护服的热防护效果有一定的影响,Mercer等[13]建立了内含相变材料的多层动态的热传递模型。考虑到水分对热防护效果的影响,Lawson等[14]进一步建立了多层织物的热湿传递模型。考虑到空气层对热防护服性能的影响,Ghazy等[15]建立了织物中包含多空气层的多层织物热传递模型。
总之,上述研究都是在Torvi模型基础上进行的改进,没有考虑到辐射的双向性。本文模型改用了不同的辐射项,综合考虑了热传导、双向辐射传热,并对3层织物(外壳、防水层和隔热层)的外壳和隔热层模型进行优化。相比其他模型,本文改进模型对热传递拟合会更符合实际过程。同时,不同模型对同一热传递过程再描述,加深了本文对纺织材料中热传递的认识,有利于进一步开展研究,为预测火场安全工作的时间和提高热防护服装的性能提供理论依据。
1 热传递模型
1.1 模型假设
图1示出由热防护服、人体皮肤及热防护服-皮肤间的空气层中组成的系统。其中,热防护服包括外壳(Kevlar®/聚苯并咪唑PBI)、防水层(透气聚四氟乙烯薄膜NOMEX)和隔热层(芳纶NOMEX)3层织物结构。织物和皮肤间的空气层厚度在6.4 mm以内[2,7]。人体的皮肤结构也可分为3层,由外而内依次为表皮、真皮和皮下组织。

图1 热防护服-空气层-皮肤系统Fig.1 System of thermal protective clothing-air gap-skin
对于热防服-空气层-皮肤系统,本文做出如下假设[2,7,15,16,18]:1)热传递沿垂直于皮肤方向进行,故可视为一维的;2)织物是各项同性的;3)能量从火焰到外壳时,包含热对流和热辐射。由于外壳阻挡了大部分的辐射,因此,在织物层和人体皮肤传递过程中,可以忽略辐射;4)空气层的厚度值不超过6.4 mm,热对流影响小,因而不考虑热对流;5)织物层之间、织物与空气层之间、空气层与皮肤之间的温度分布都是连续变化的,但温度梯度是跳跃的;6)表皮的外表温度为32.5 ℃,皮下组织的底部和人体的核心体温是37 ℃,皮肤内部温度可由插值近似表达;7)血液的对流换热过程发生在有毛细血管中的肌层内,毛细管区内肌肉和血液温度等于肌肉组织的温度;8)局部毛细血管的血液灌注率是各向同性的。
1.2 数学模型
1.2.1热防护服中的热传递
基于以上假设,本文给出三层热防护服的热传递模型[17]:
(1)
(2)
(3)
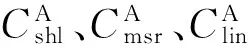
热辐射量[17]满足:
(4)
(5)
式中:β为辐射吸收常数,K-1;σ为斯蒂芬-波尔兹曼常数,5.670 ×10-8W/(m2·K4)。
织物层的初始条件:
T(x,0)=TI(x),x∈(0,Lfab)
(6)
织物层的左右边界条件[2]分别为

(7)
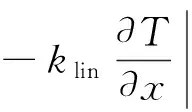
(8)
(1-ξ1)FL(0,t)+ξ1σT4(0,t)=FR(0,t)
(9)
式中:ξ1为外壳左侧的辐射率,W/(s·m2);qair为来自隔热层背面的热辐射热流密度,W/m2;kair为空气的热传导率,W/(m·K)。
外壳与防水层之间的接触面满足:
Tmsr|x=Lshl=Tshl|x=Lshl
(10)
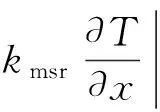
(11)
(1-ξ2)FL(Lshl,t)+ξ2σT4(Lshl,t)=FR(Lshl,t)
(12)
式中,ξ2为外壳右侧的辐射率,W/(s·m2)。
防水层与隔热层之间的接触面满足:
Tlin|x=Lshl+Lmsr=Tmsr|x=Lshl+Lmsr
(13)
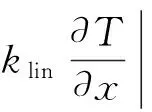
(14)
从文献[9]可知,式(7)中从火焰到织物辐射和对流的热通量可描述为
(qconv+qrad)|x=0=hc,fl(Tg-T|x=0)
(15)
式中:qconv为火焰到外壳的热对流密度,W/m2;qrad为火焰到外壳的热辐射密度,W/m2;hc,fl为火焰和外壳外表面之间的热对流系数,W/(m2·K);Tg为火焰温度,K。
当环境温度变化幅度不大时,抛物方程(1)、(2)、(3)的显热容CA和热传导率k均近似看成常量。超高温度将造成显热容和热传导率的变化,对显热容的影响尤其大。在这种高温环境下,若采用常量将造成较大的误差结果,因此,本文作出如下处理。
在多层热防护服的热传递模型中,采用了显热容法来描述织物的比热变化,显热容[2]的计算公式为
CA=ρcp
(16)
式中:ρ为对应织物的密度,kg/m3;cp为相应织物的比热,J/(kg·K)。
cp=1 300+1.6(T-300)
(17)
本文给出有效热传导率进行计算:
(18)
(19)
(20)
(21)
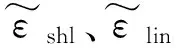
1.2.2空气层中的热传递
根据假设,可以得到空气层的热传递模型[15]:
(22)
其中,Ω4=(Lfab,Lfab+Lair)。
由于空气层厚度狭小,可将其看成一个矩形封闭腔,利用有限空间内传导/对流传热原理,综合考虑空气中传导/对流和织物辐射作用,由此假定空气层的传导是稳态,辐射可看成一种表面现象;因此,本文可把上述空气层模型解耦成如下模型[9]:
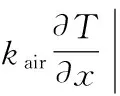
(23)
(24)
式中:εlin、εskin分别为隔热层和皮肤的发射率;hc,air为外部环境中空气传导和自然对流的对流换热系数,W/(m2·K)。
(25)
式中,Nu为努塞尔特数。
空气层的初始条件为
T(x,0)=TI(x),x∈Ω4
1.2.3皮肤中的热传递
结合皮肤组织结构,分别为表皮、真皮和皮下组织。本文采用Pennes的生物热传递模型[18]:
(x,t)∈Ω5×(0,texp)
(26)
式中:kskin为皮肤的热传导率,W/(m·K);ωb为血液灌注率,m3/(s·m3);Tcr为人体核心温度,310.15 K。
Ω5=(Lfab+Lair,Lfab+Lair+Lskin),
Lskin=Lep+Lds+Lsc。
式中,Lep、Lds、Lsc分别为表皮、真皮和皮下组织的厚度,m。
皮肤的左右边界分别为
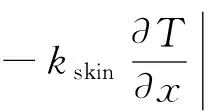
(27)
T|x=Lfab+Lair+Lskin=Tcr
(28)
皮肤层的初始条件为
T(x,0)=TI(x),x∈Ω5
2 皮肤烧伤程度表示
为了预测达到皮肤烧伤的时间,以改善热防护服系统的性能,本文采用Henriques积分[19]作为评判标准,当基底层(即表皮和真皮的接触面)的绝对温度达到317.15 K时,皮肤发生热损伤。为预测皮肤的各级烧伤程度,将接触面的温度代入以下积分表达式:
(29)
式中:ψ为烧伤损伤在接触面或者任意深度的皮肤的定量测量;P为频数因子,s-1;ΔE为皮肤的活化能,J/kmol;R为理想气体常数,J/(mol·K);T为在基底层或在皮肤内的任何深度的绝对温度,K;t为T达到317.15 K后的持续时间,s。
积分表达式(29)关于积分的时间区间是取接触面温度超过317.15 K之后的时间。
对于一级和二级烧伤,T取基底层的温度。当ψ|x=Lfab+Lair+Lep≤0.53时,将不会发生烧伤;当0.53<ψ|x=Lfab+Lair+Lep≤1 时,将发生一级烧伤;当ψ|x=Lfab+Lair+Lep>1时,将发生二级烧伤。
对于三级烧伤,积分方程的T取真皮基(即真皮层和皮下组织的接触面)的温度。当这个接触面满足ψ|x=Lfab+Lair+Lep+Lds>1时,将发生三级烧伤。
3 热传递模型数值算法
本文采用有限差分法来解决以多层热防护服、空气层和人体皮肤为整体的偏微分方程组。辐射项的边界条件和随温度变化的对流系数的存在,造成了偏微分方程组的非线性,本文采用显隐式方法来解决。具体计算方法如下:
外壳及其左边界的偏微分方程为
(30)
其中,
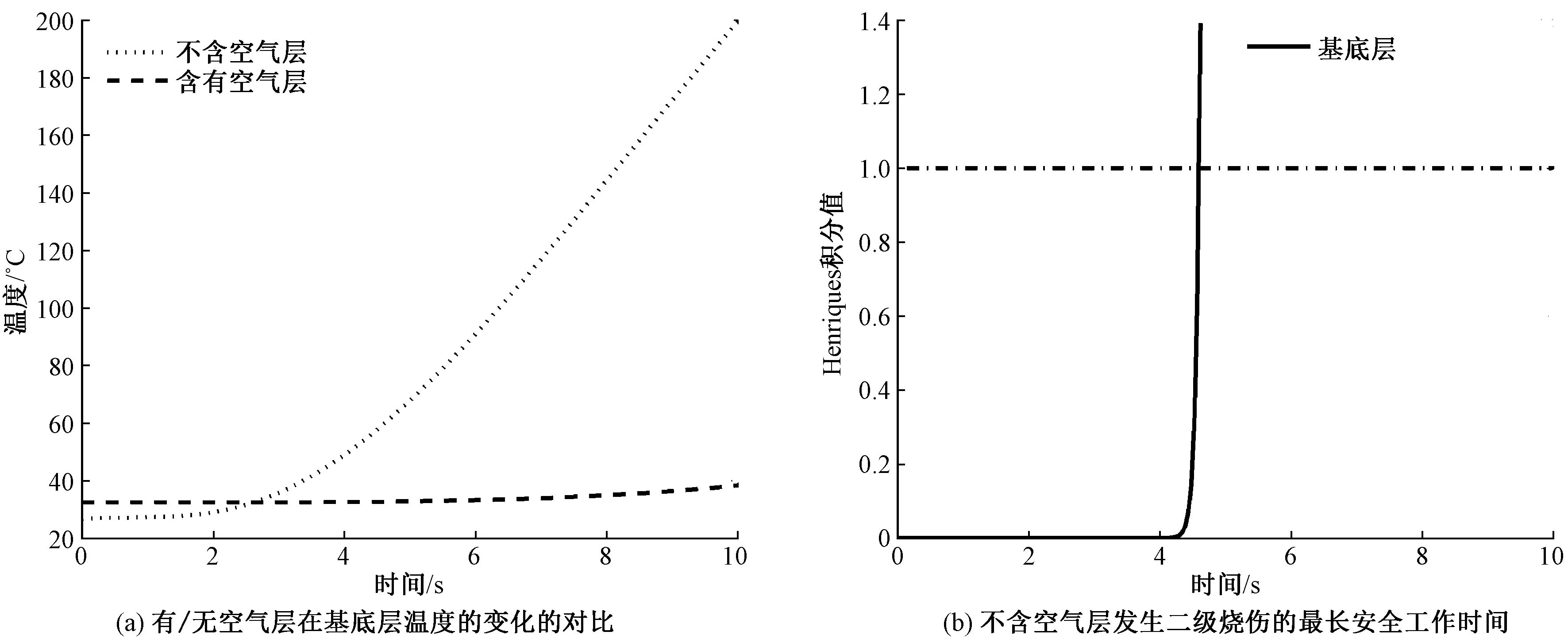
将外壳离散为m1+1点,分别为0=x0 图2 改进模型和Ghazy模型在织物层外表面的温度对比Fig.2 Comparison of present simulation and Ghazy′s model′s results of temperature histories on surface of fabric layer.(a) Ghazy′s model′s results of temperature changes on outer surface of three-layer fabric; (b)Modified model′s results of changes on outer surface of three-layer fabric; (c)Ghazy′s model′s results of temperature changes on fabrics; (d) Modified model′s results of temperature changes on fabrics 可证明以上方法是有条件稳定的,且在一定条件[20]下收敛速度为O(τ+h2)。 类似地,将左边界条件离散得 或者 式中,ω=hc,flh/kshl。 采用同样的方法,本文可以将其他织物层(式(2)、(3))和皮肤层(式(26))及其边界做处理。当已知皮肤层的温度后,由Henriques和Moritz给出的积分方程(式(29))可计算出在高温条件下人体皮肤达到各级烧伤的临界时间。 将本文模型与Ahmed Ghazy等[15]的模型和实验数据进行比对,以验证本文模型的可靠性。Ghazy假定织物暴露在温度为2 000 K,热通量约为83 kW/m2的环境中,图2示出改进模型和Ghazy模型织物外表面在10 s内的温度对比结果。由图可知,无论是3层织物的温度随时间、位置变化图,还是3层织物各个外表面的温度随时间变化图,其数值结果都是相似的。3层织物的热物理属性,初始条件和热辐射属性[15]见表1、2。另外,织物火焰和皮肤的放射率分别为0.9、0.02和0.95。 表1 织物的热物理属性Tab.1 Thermophysical/geometrical properties of fabric 表2 织物和空气层的初始条件Tab.2 Initial conditions for fabric and air gap 由于对空气层和皮肤的模型做了简化处理,本文对新建立的模型与Ghazy的实验结果进行相应的比较。表3示出皮肤的热物理属性。图3示出前10 s内新建立的模型与Ghazy的模型皮肤层的温度对比。 表3 人体皮肤的热物理属性Tab.3 Thermophysical properties of human skin 注:比热单位为J/(kg·K),热传导率单位为W/(m·K),血液灌注率单位为m3/(s·m3)。 由图3可知,在同等条件下,新建模型的结果和Ghazy的模型在前10 s 的结果是一致的。由于图3(a)中,10 s后的结果是暴露结束后的数据,不在本文考虑的范围内,因此,本文不做相应的对比。 总之,当前的改进模型和Ghazy的模型和数据的比对效果非常好。改进模型考虑到辐射的双向性,更加符合持续高温中多层热防护服的热传递过程。 图3 前10 s内改进模型和Ghazy模型皮肤层的温度对比Fig.3 Comparison of modified simulation and Ghazy′s system with air gap within former 10 s.(a)Ghazy′s model;(b) Modified model 本文利用热防护服-空气层-皮肤系统结合Henriques皮肤烧伤判断标准来预测到达一级、二级和三级烧伤的临界时间,即织物持续暴露在闪火环境中,达到各级烧伤的最长安全工作时间。表4示出计算Henriques积分所需的参数。 表4 P和ΔE/R的数值Tab.4 Values of P and ΔE/R 图4 热损伤时间及各级烧伤的最长安全工作时间Fig.4 Determination of longest safety work time for burns from modified model. (a) Temperature histories on basal layer;(b) Longest safety work time for first- and second-degree burn from modified simulation;(c) Temperature histories on basal layer;(d) Longest safety work time for third-degree burn from modified simulation 图4示出开始热损伤的时间和达到各级烧伤的最长安全工作时间。从图4(a)可知,12.85 s时皮肤就要发生热损伤。从图4(b) 可知,达到一级和二级烧伤的最长安全工作时间分别为17.10、17.32 s。 图5 改进模型有无空气层的对比Fig.5 Comparison of modified simulation with or without air gap. (a)Comparison of temperature histories on basal layer with or without air gap; (b) Longest safety work time on second-degree burn from modified model without air gap 上述结果表明,在以上条件下,暴露时间若小于12.85 s 皮肤不发生任何热损伤的,当发生热损伤后需4.25 s发生一级烧伤。同时,对比一级烧伤和二级烧伤的最长安全工作时间可看出,在持续的高温条件下,皮肤发生一级烧伤后,很快就会发生二级烧伤。从图4(c)、(d)可知,真皮基达到44 ℃需要20.10 s,且在28.14 s达到三级烧伤。对比图4(a)、(c)可发现,无论是在基底层还是真皮基,只要温度达到55 ℃左右,将分别发生二级烧伤和三级烧伤。比较图4(b)、(d)发现,在到达最长安全工作时间后,曲线将变得非常陡峭,这说明损伤程度加深速度非常快。同时,考虑到热防护服内蓄热等因素,实际的最长安全工作时间可能小于预测值。以上数值模拟结果表明,在紧急而恶劣的闪火环境中,即使身着热防护服也只有十几秒的安全时间。 图5示出改进模型中存在或不存在空气层2种情况的预测结果。 在高温情况下,没有空气层相比存在空气层而言,基底层的温度将会迅速提高。没有空气层时,达到二级烧伤的最长安全工作时间仅为4.59 s,而存在空气层(见图4(b))时的时间为17.32 s。产生这种差别的主要原因是空气的导热系数明显小于常见的纺织材料,是理想的绝缘体,因此,空气层的存在与否及其厚度将直接影响热防护服的防护性能。 本文对外壳和隔热层进行改进,表5示出不同厚度的外壳和隔热层对热防护属性的影响。可以看出,织物越厚,最长安全工作时间越长。这是由于织物厚度变大,热阻也会相应变大,同时,越厚的织物有更好的储热能力,使得热通量不至于灼伤皮肤。然而,现实中如果织物过厚,不仅太过沉重,不易穿戴,给高温工作者造成负担,而且越厚的织物拥有更好的储热能力,以致于在离开火场时给人体造成不同程度的烧伤,长时间穿着甚至造成三级烧伤。 表5 不同织物厚度及其产生二级烧伤的最长安全工作时间Tab.5 Fabric thickness and predicted minimum exposure time capable of generate second-degree burn 在高温条件下,本文对已有的热防护服热传递模型进行了改进,并且与Ghazy的模型以及相应的实验数据进行比对,说明模型的合理性。应用该模型预测了织物层和皮肤层的温度随时间的变化规律,同时用其来预测各级烧伤的最长安全工作时间,为实际的高温作业者提供有用的安全知识。从实验结果可知,空气层可延长热量传递到皮肤的时间,起到保护作用。织物越厚,防护性能越好。 本文只考虑了空气层和织物厚度对防护效果的影响,而其他参数对防护效果的影响还需进一步研究。再者如何优化参数来提高热防护服防护效性能将是下一步研究的方向。 [1] BARKER R L. A review of gaps and limitations in test method for first responder protective clothing and equipment [R]. [S.l.]:National Personal Protection Technology Laboratory,2005:8-13. [2] TORVI D A.Heat transfer in thin fibrous materials under high heat flux conditions[D].Edmonton: University of Alberta,1997:1-134. [3] STOLL A M, GREENE L C. Relationship between pain and tissue damage due to thermal radiation[J]. Journal of Applied Physiology, 1959, 14(14):373-382. [4] TAKATA A. Development of criterion for skin burns[J]. Aerospace Med,1974,45(6):634-637. [5] GIBSON P. Multiphase heat and mass transfer through hygroscopic porous media with applications to clothing materials[J]. Fiber,1996, 53(5):183-194. [6] TORVI D A, DALE J D. Heat transfer in thin fibrous materials under high heat flux[J]. Fire Technology, 1999, 35(3):210-231. [7] 朱方龙. 服装的热防护功能[M]. 北京:中国纺织出版社, 2015:98-131. ZHU FangLong.Clothing Thermal Protection Function[M].Beijing:China Textile & Apparel Press, 2015:98-131. [8] SAWCYN C M J, TORVI D A. Improving heat transfer models of air gaps in bench top tests of thermal protective fabrics[J]. Textile Research Journal, 2009, 79(7):632-644. [9] CHITRPHIROMSRI P, KUZNETSOV A V. Modeling heat and moisture transport in firefighter protective clothing during flash fire exposure[J]. Heat and Mass Transfer, 2005, 41(3):206-215. [10] SONG G. Modeling thermal protection outfits for fire exposures[D]. Raleigh:North Carolina State University,2002:1-100. [11] GHAZY A, BERGSTROM D J. Numerical simulation of the influence of fabric′s motion on protective clothing performance during flash fire exposure[J]. Heat and Mass Transfer, 2013, 49(6):775-788. [12] MELL W E, LAWSON J R. Heat transfer model for fire fighter′s protective clothing[J]. Fire Technol, 1999, 36: 39-68. [13] MERCER G N, SIDHU H S. Mathematical modelling of the effect of fire exposure on a new type of protective clothing[J]. Australian & New Zealand Industrial & Applied Mathematics Journal, 2007, 49:289-305. [14] LAWSON J R, MELL W E, PRASAD K. A Heat Transfer model for firefighters′ protective clothing: continued developments in protective clothing mode-ling[J]. Fire Technology, 2010, 46(4):833-841. [15] AHMED GHAZY, DONALD J BERGSTROM. Numerical simulation of heat transfer in firefighters′ protective clothing with multiple air gaps during flash fire exposure[J]. Numerical Heat Transfer Applications, 2012, 61(8):569-593. [16] XU D, WEN L, XU B. An inverse problem of bilayer textile thickness determination in dynamic heat and moisture transfer[J]. Applicable Analysis, 2014, 93(3):445-465. [17] FAN J, LUO Z, LI Y. Heat and moisture transfer with sorption and condensation in porous clothing assemblies and numerical simulation[J]. International Journal of Heat and Mass Transfer,2000,43: 2989-3000. [18] PENNES H H. Analysis of tissue and arterial blood temperatures in the resting human forearm[J]. Journal of Applied Physiology, 1998, 85(1):5-34. [19] HENRIQUES F C, MORITZ A R. Studies of thermal injuries: I: the conduction of heat to and through skin and the temperatures attained therein[J]. Am J Pathol, 1947, 23(4): 531-549. [20] YU Y, XU D, XU Y S, et al. Variational formulation for a fractional heat transfer model in firefighter protective clothing[J]. Applied Mathematical Modelling, 2016, 40(23-24):9675-9691.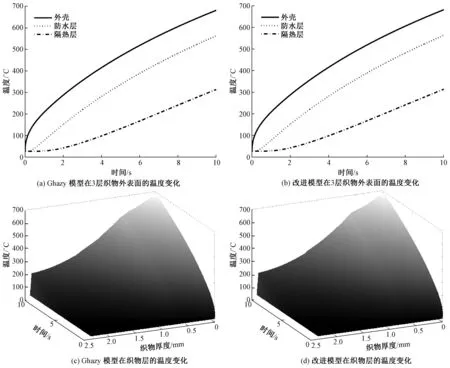

4 模型验证



5 模型应用
5.1 临界时间与最长安全工作时间


5.2 空气层与织物变量对防护性能的影响

6 结束语
