New Method for Estimating Daily Global Solar Radiation over Sloped Topography in China

Guoping SHI,Xinfa QIU,and Yan ZENG

1School of Geography and Remote Sensing,Nanjing University of Information Science and Technology,Nanjing 210044,China

2School of Applied Meteorology,Nanjing University of Information Science and Technology,Nanjing 210044,China

3Jiangsu Climate Center,Nanjing 210009,China

1.Introduction

Accurate computation of solar radiation over sloped surfaces is important to agriculture and high-resolution weather prediction(Tian et al.,2001;Manners et al.,2012).Although there have been many studies on determining the solar radiation overflat horizontal surfaces,research on sloped surfaces is limited due to the complicated topography involved and a lack of observations.The solar radiation over a sloped surface is not only influenced by the atmosphere but also by slope orientations relative to the sun,terrain shading and skyview,which can vary sharply in space and time,making the calculation of solar radiation extremely complicated.

Geographical information system(GIS)and remote sensing techniques have provided solutions to these problems.In thisfield,a digital elevation model(DEM)can be used to obtain geographical factors such as longitude,latitude,altitude,slope,aspect etc.,which are the necessary variables required for the determination of solar radiation over sloped surfaces.Williams et al.(1972),Bocquet(1984),Dozier and Frew(1990),Li et al.(1999)and Yeom et al.(2016)all used DEM data to compute the solar radiation in mountainous areas.Qiu et al.(2005,2008)used a DEM to investigate numerical calculations of monthly global solar radiation and direct and diffuse radiation over actual terrain.The simulation results were able to reveal the underlying variation of solar radiation with changes in topography.However,on the daily scale,the shadow effect of rugged terrain is more complicated,and ground-reflected radiation was considered in early studies using rather simple algorithms(He et al.,2003;Wang et al.,2004;Li and Li,2007).

In this paper,we introduce a new method to determine solar radiation over sloped terrain.The method uses the physical scheme developed by Iqbal(1983)to determine the solar radiation over a horizontal surface under clear-sky conditions.The effect of clouds is considered using the sunshine duration estimated from MODIS data.These horizontal radiation data are then corrected using a topographical scheme that includes the effects of terrain based on DEM data.The method is used to determine daily solar radiation over sloped terrain in China and is named Grid-MetDaily Radiation(GMDR).The characteristics of the daily distribution of solar radiation over sloped surfaces in China are determined and analyzed using this method.

Therestofthepaperisorganizedasfollows:Section2in- troduces the method used to develop the GMDR model.Section 3 describes the data used in this study.Section 4 presents an evaluation of the GMDR model against observations.Section 5 describes the distribution of solar radiation over sloped surfaces in China.Section 6 gives the conclusions.

2.Method

The purpose of this study is to develop a model to estimate daily global solar radiation over sloped terrain.This work includes two parts:determination of global solar radiation over a horizontal surface(GRHS),and determination of global solar radiation over a sloped surface(GRSS).

2.1.Determination of GRHS

GRHS can be determined using existing methods.For example,Weng(1964)proposed a simple method based on the percentage of sunshine duration:

where Q0is the solar radiation at the top of the atmosphere(TOA),s is the percentage of sunshine duration,and a and b are empirical coefficients.Equation(1)has been widely used in China since its introduction.In our study,Q0is replaced with Qclr:

where Qclris defined as an idealized clear-sky GRHS.It includes the effects of gaseous absorption and Rayleigh scattering,while the effects of aerosol and cloud are still considered in the term(a+bs).In the original Eq.(1),the input variable is only sunshine duration,which reflects the effect of cloud.All other factors of influence are implicitly included in thefitting coefficients.Such a treatment makes Eq.(1)highly localized and the coefficients a and b are not uniform in space and time.This deficiency can be significantly improved in Eq.(2)because most factors of influence under clear-sky conditions are explicitly treated in the calculation of Qclr,and the coefficients a and b rely heavily on the aerosol and cloud.

Iqbal(1983)developed a scheme to estimate Qclr,which is adopted in this study.In the Iqbal scheme,Qclris determined by

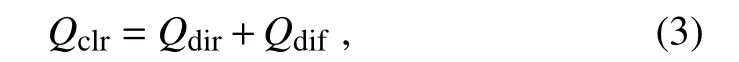
where Qdiris the direct solar radiation(DIR)and Qdifis the diffuse solar radiation(DIF).The transmittances of DIR for water vapor,ozone,uniformly mixed gases,Rayleigh scattering,and aerosols are parameterized in terms of relative humidity,surface temperature,surface pressure,and ozone optical path length.The DIF is determined by the diffuse downward component due to Rayleigh scattering and the downward component due to multiple reflections between the surface and atmosphere.Since aerosol data are difficult to implement in this work,we do not explicitly consider the effects of aerosol.The aerosol transmittance in the Iqbal model C(Iqbal,1983)is set to 1.Thus,the effects of aerosol are not included in the idealized clear-sky term Qclr.However,the effects of aerosol are not ignored.Because we use the observational data to determine the coefficients a and b in Eq.(2)(see next section),the effects of aerosol and all other unknown factors of influence are implicitly included in these coefficients.A detailed description of the Iqbal model C is presented in the Appendix.

2.2.Determination of GRSS

The clear-sky GRSS is determined by three components,

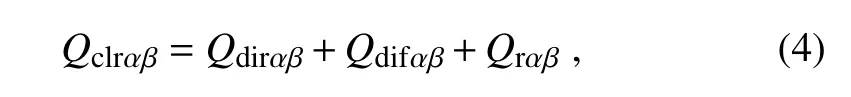
where Qclrαβis the clear-sky GRSS,Qdirαβis the DIR over the sloped surface,Qdifαβis the DIF over the sloped surface,and Qrαβis the reflected solar radiation over the sloped surface.The subscripts α and β represent the slope and aspect of the terrain.

To determine Qdirαβ,we assume

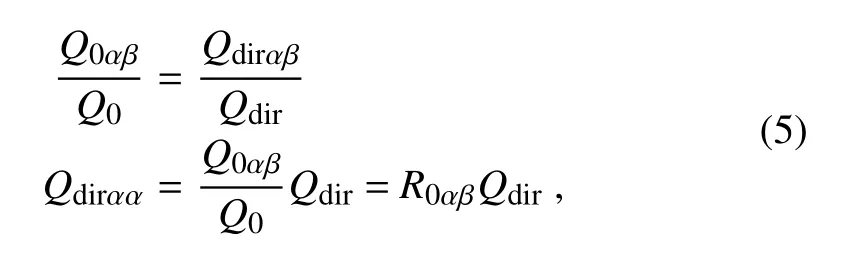
where Q0αβand Q0are the TOA solar radiation over the sloped and horizontal surface,respectively;and R0´aβis the ratio of TOA radiation over the sloped surface to that over the horizontal surface.Thus,the effects of slope,aspect,and topographic shadow are represented by R0αβ,which can be determined using the DEM–as described by Qiu et al.(2005).A brief description of the determination of Q0αβis given here.According to Qiu et al.(2005),the daily total Q0αβover complex terrain can be calculated by

where T is the daylight length,(r0/r)2is the eccentricity correction factor of Earth’s orbit;r and r0are the sun–earth distance and mean sun–earth distance,respectively;I0is the solar constant;δ is the solar declination;ω is hour angle;bl and el are the start and end,respectively,of the sunshine in the lth period;m is the number of periods during which there is sun illumination;α is the slope angle;β is the slope orientation;and ϕ is the latitude.With the topographical factors provided by the DEM system and the number of sunshine periods m,Q0αβcan be determined by Eqs.(6)–(9).

Similar to Eq.(5),we derive an expression for the diffuse component,

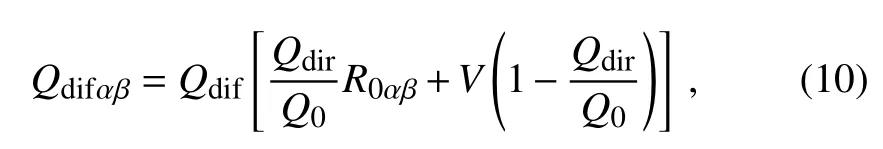
where V is the terrain openness.The method for determining V is described in Qiu et al.(2008).Finally,the reflected radiation from the sloped surface can be computed by the following expressions:

where ρgis the surface albedo,which can be estimated using the planetary albedos of AVHRR channels 1 and 2(ρCH1and ρCH2,respectively),as described by Valiente et al.(1995):

The GRSS is determined by:

where Qαβis the GRSS.

2.3.Determination of sunshine duration

The percentage of sunshine duration is a key variable in this study because it reflects the important effects of cloud.This variable is routinely available from operational observations,so the data are usually used to determine the values at other locations using interpolation.However,the method of interpolation is not very accurate.For this reason,we use MODIS cloud products to estimate the sunshine duration,because the spatial resolution of MODIS cloud products is moderate.Based on the cloud fraction and percentage of sunshine duration data measured at 682 meteorological stations in China in 2003,we establish the following empirical relationship(Shi et al.,2013;He et al.,2014):

where C is the daily mean cloud amount and asand bsare empirical coefficients.

3.Data and study area

3.1.Conventional meteorological data

The daily global solar radiation and sunshine duration data measured at 98 radiation stations from 1961 to 2000 in China are used to determine the coefficients in Eq.(2).The coefficients for each station on each day of the year are determined using the daily data from these 40-year records.These coefficients are then interpolated to 1 km×1 km spatial grids using the inverse distance weighted method and stored in a database for use in the determination of GRHS and GRSS.In addition,temperature,relative humidity and surface pressure are required using the Iqbal model for the determination of clear-sky radiation.These data at 682 stations in 2003 are collected and interpolated onto 1 km×1 km grids for thefinal calculations.The reason for using these 2003 data is that thefinal calculations require MODIS cloud fraction data,and these are only available after 2002(i.e.data for the whole of 2003 are available).The sunshine duration data from intensive observation stations in 2003 are used to test Eq.(14)using the MODIS cloud fraction data(https://ladsweb.nascom.nasa.gov/search).

3.2.DEM data

A DEM is a simulated digital representation of terrain elevation across regular grids within a certain range and reflects the spatial distribution of regional morphology.DEM data at the spatial resolution of 1 km×1 km are obtained from the National Geomatics Center of China(http://ngcc.sbsm.gov.cn/article/en/or/an/)and used to determine the effects of height,slope and aspect on GRSS.

3.3.MODIS data

MODISisascanning instrumentthattakesmeasurements in 36 spectral bands from visible to thermal infrared.MODIS instruments are onboard two polar-orbiting NASA satellites:Terra,which has a daytime equatorial crossing at about 1030 LST and 2230 LST;and Aqua,which has an equatorial crossing at about 0130 LST and 1330 LST.Therefore,MODIS provides measurements four times a day.The MODIS cloud mask is classified into four groups based on threshold values in multispectral channels,which are closely related to different surface types at each given pixel:group 1 is “confi-dently clear”;group 2 is “probably clear”;group 3 is “probably cloudy”;and group 4 is “cloudy”.The MODIS global level-2 dataset provides cloud fractions derived by averaging 5×5km2pixels(Platnicketal.,2015).Thesedataarefurther averaged to daily means and used in this study to estimate the sunshine duration.

3.4.Test areas

To test the performance of our scheme,four mountainous areas are chosen as study areas,and their geographic zones and climate characteristics are given in Table 1 and also shown in Fig.1.As indicated by the rectangles in Fig.1,these zones are essentially east–west-oriented,and therefore the contrast in radiation between northern and southern slopes should be clear.

4.Validation of the method

To test the accuracy of the methods presented in section 2,the following four statistical parameters–mean absolute bias(MAB),mean relative absolute bias(MRAB),root-meansquared error(RMSE)and relative root-mean-square error(rRMSE)–are used to measure the performance of these equations:

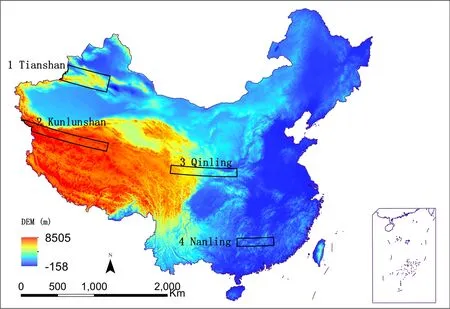
Fig.1.The DEM and analysis areas in China(1 km×1 km).

Table 1.Study areas and their climate characteristics.

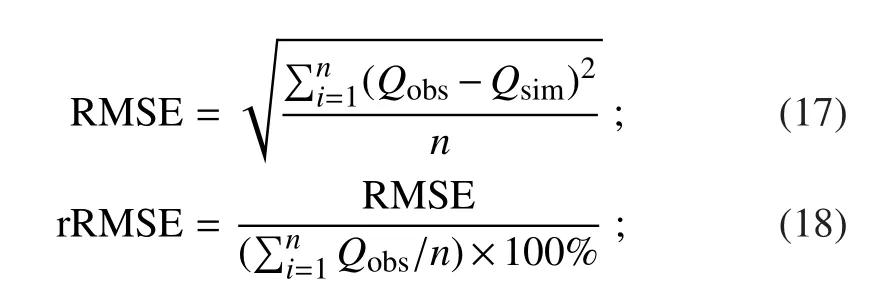
where Qobsis the observed solar radiation,Qsimis the simulated value,and n is the number of samples.

Webeginbyevaluatingtheaccuracyofthesunshineduration estimated using Eq.(14).The MAB for the curvefitting of Eq.(14)using the data from 682 statios is 0.044.We further test this equation using the sunshine duration data from intensive meteorological stations in 2003[data not used in the curvefitting of Eq.(14)].The MODIS cloud fraction is at a 5 km×5 km grid resolution and the daily mean values are used to calculate the sunshine duration using Eq.(14).The grid results corresponding to the locations of the intensive observation stations are compared with the observations.Figure 2 shows scatter and histogram plots between the modelled and observed percentage of sunshine duration.The data points are considerably scattered,but a linear relationship between the measured and modelled values is evident.The histogram shows that the model error follows a normal distribution with a maximum frequency falling in the zero interval.The MAB using independent data from these intensive observation stations is 0.097,while the RMSE and rRMSE are 0.106 and 15.45%,respectively.The mean bias of the interpolation method is 0.251.These results indicate that using the cloud fraction to estimate the sunshine duration is better than the interpolation method.Figure 3 shows the distributions of the percentage of sunshine duration on 15 January,15 April,15 July and 15 October 2003,determined using the MODIS cloud fraction data.This figure clearly reflects the cloud distributions over the country,and so we use it as a reference to analyze the solar radiation distributions presented below.

Next,we compare the modelled results for clear-sky conditions with observations.Equation(2)is used to calculate the GRHS on the 15th of each month from 1961 to 2000 for the 98 radiation stations.The modelled and observed GRHSs corresponding to a percentage of sunshine duration greater than 90%are selected as the clear-sky results,and these results are shown in Fig.4.It is apparent that Eq.(2)can produce clear-sky results that are in reasonably good agreement with observations.The correlation coefficient between the modelled and observed values is 0.995.The MRAB and rRMSE are 6.93%and 9.14%,respectively.

A comparison between the modelled and observed GRHS values under all-sky conditions is shown in Fig.5a,in which we can see that the modelled GRHS is also highly correlated with observations(the correlation coefficient between them is 0.94).The statistical results are presented in Table 2.The meansimulationbiasforthe98solarradiationstationsis1.51 MJ m−2d−1and the relative bias is 10.57%.The observational GRHS data in 2003 are further used to test the GMDR model.These data are not used in the development of the model,so the test is independent.Figure 5b shows the same comparison,but using the independent data in 2003.The correlation coefficient for the results in this period is also 0.94.The RMSE and rRMSE for this test are 2.16 and 13.43%,respectively.

Fig.2.Comparison of the modelled percentage of sunshine duration using the MODIS cloud fraction with observations from intensive meteorological stations in China.The right-hand panel shows a histogram of the difference between the modelled values and the observations.

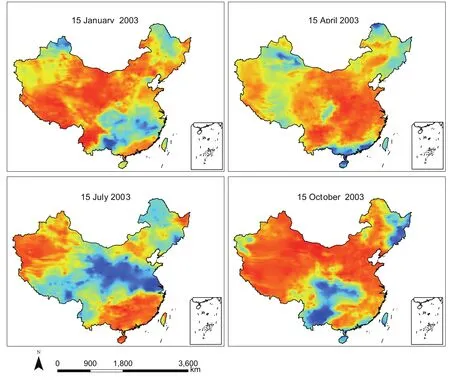
Fig.3.Percentage of sunshine duration determined using the MODIS cloud fraction on 15 January,15 April,15 July and 15 October 2003.

Table 2.Statistical testing results for global solar radiation under all-sky conditions.

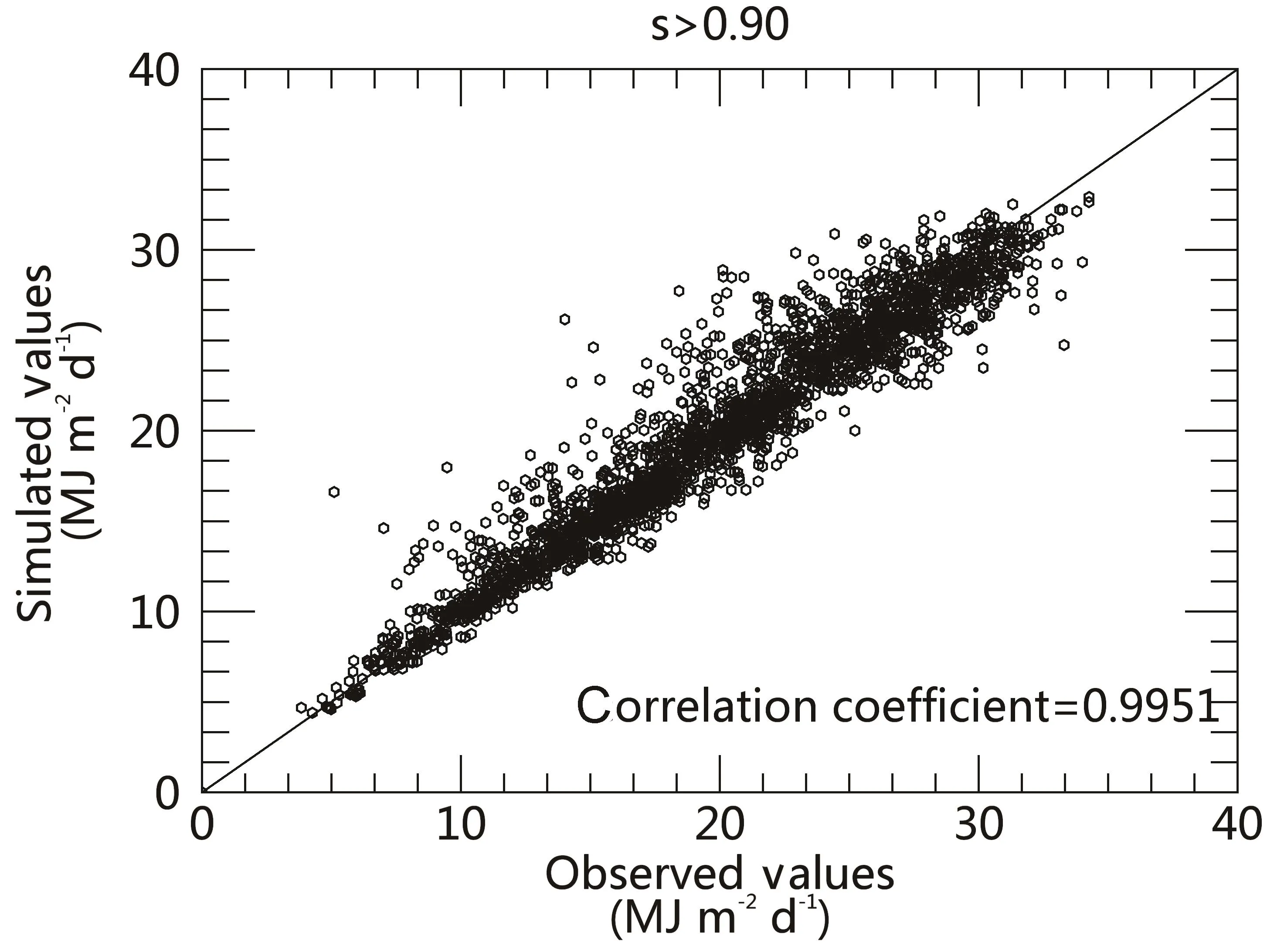
Fig.4.Comparison of clear-sky daily global solar radiation determined using Iqbal model C with observations during 1961–2000 at 98 radiation stations.The clear-sky observations are collected if the percentage sunshine duration is greater than 90%.Units:MJ m−2d−1.

5.Simulation of GRSS

The daily GRSS over China is calculated using Eq.(13)for four days of each season in 2003.Figure 6 shows the distribution of daily GRSS on 15 January,15 April,15 July and 15 October 2003 using 1 km×1 km gridded data.As we can see,the highest GRSS values appear over the Tibetan Plateau and Yunnan-Guizhou Plateau on 15 January,due to the relatively clearer-sky conditions(refer to Fig.3).The lowest values,over Heilongjiang and north of Xinjiang,are due to the combination of low sunshine duration and small insolation at higher latitudes.Lower values are also seen over the southeast region due to low amounts of sunshine duration in these areas.On 15 April,a low GRSS zone occurs over the Tibetan Plateau,and this is due to the effect of cloud,as seen in the same region in Fig.3.On 15 July,a low GRSS belt occupies areas from the eastern coast to the western Qinghai-Xizang Plateau.Such a distribution is clearly due to the effects of cloud cover in these areas,because a low-value belt of sunshine duration in July also occurs in the same areas.On 15 October,a similar relationship between the distribution of sunshine duration and GRSS to the other three days can be identified.

6.Local distribution characteristics and effects of geography and topography

The comparison between Fig.3 and Fig.6 clearly demonstrates that cloud has a dominant effect on GRSS.The effects of topography are completely masked if cloud is present.These effects are also hard to see,even in clear-sky areas,due to the scale of thefigures.To identify the effects of the slope and aspect of the topography,we choose four east–west-oriented mountain ranges(mentioned previously)as testbeds.To present the results clearly,the highlighted rectangles in Fig.1 have been enlarged,and the results under clear-sky conditions corresponding to one of these zones are presented below.

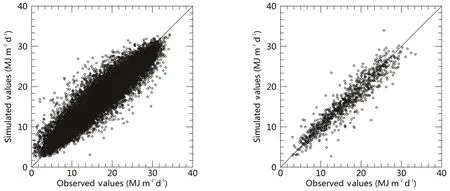
Fig.5.Comparison of modelled global solar radiation with observations at 98 stations from 1961 to 2000(left)and in 2003(right).

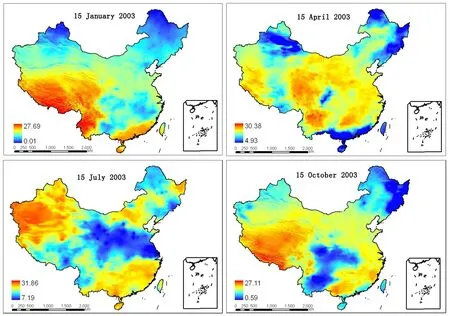
Fig.6.Spatial distribution of daily GRSS in China on 15 January,15 April,15 July and 15 October 2003(units:MJ m−2d−1).

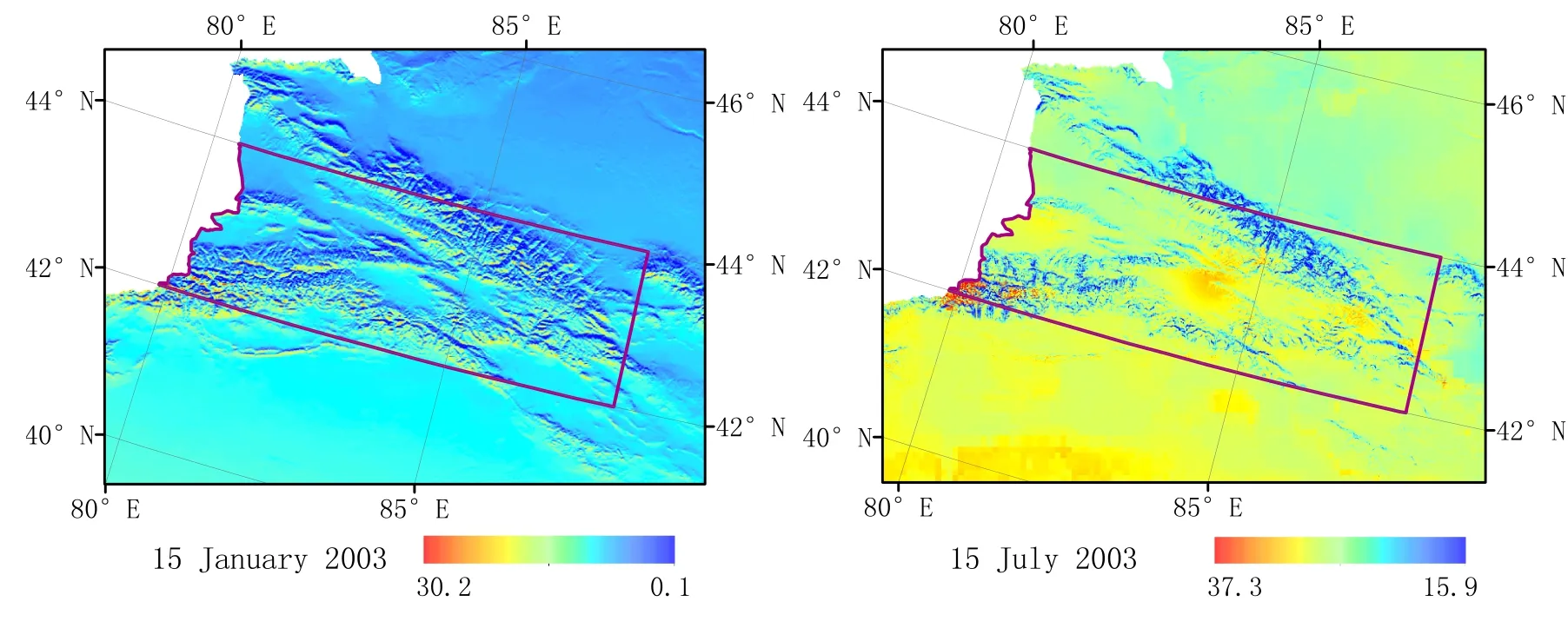
Fig.7.Partially enlarged details of clear-sky GRSS at Tianshan Mountains(longitude:79◦–88◦E and latitude:42◦–44◦N)(units:MJ m−2d−1).

Figure 7 shows the clear-sky GRSS at Tianshan Mountains on 15 January and 15 July 2003.The influence of topography on the GRSS is evident in these enlarged maps.“Warm”colorsappearoverthesouthernslopeand“cold”colors over the northern slope,meaning the GRSS is greater on former than the latter.

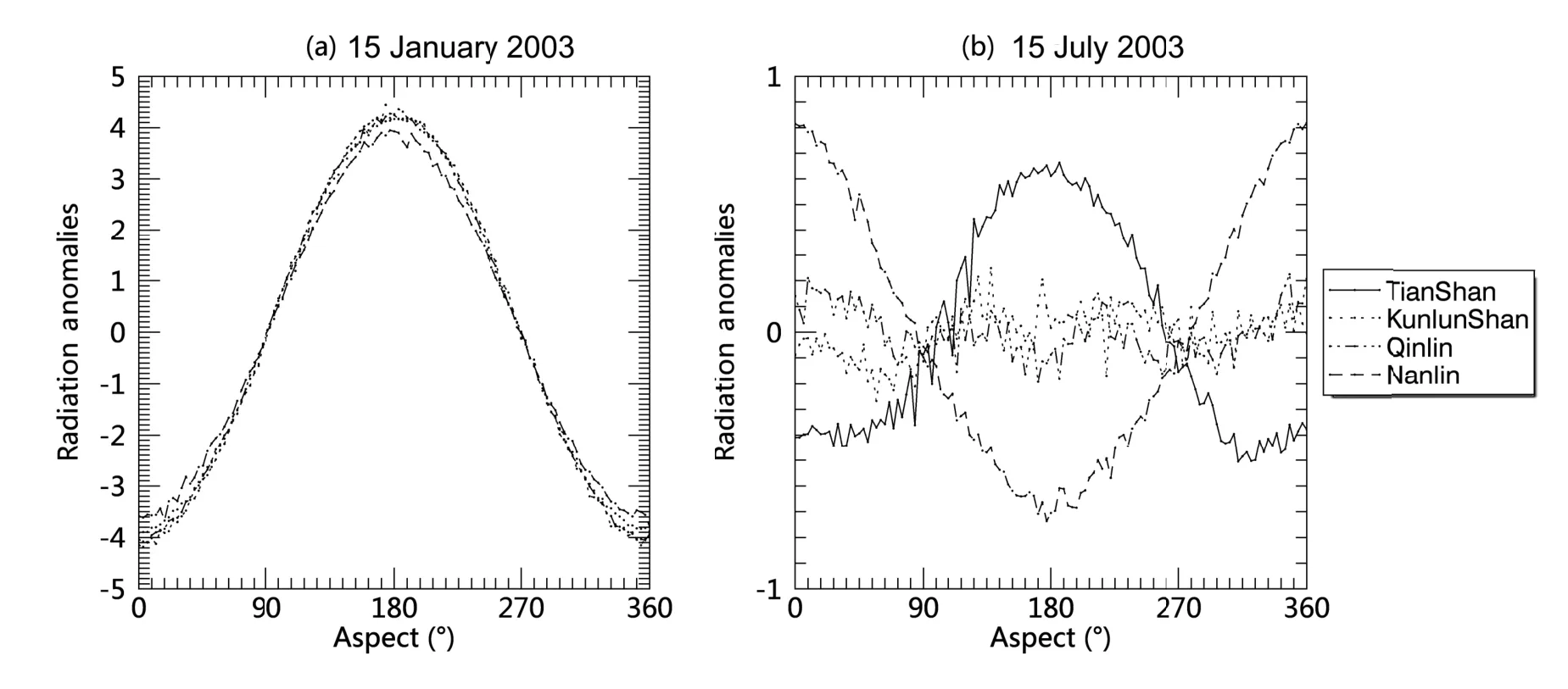
Fig.8.Variation of a clear-sky GRSS anomaly with azimuth angle for four mountainous areas on(a)15 January 2003 and(b)15 July 2003,at a slope of 10◦(0◦and 180◦represent north and south,respectively).

Fig.9.Variation of GRSS with altitude at four mountainous sites on 15 January and 15 July 2003.

To analyze the effects of azimuth and elevation on GRSS,the results from the four selected range zones for each azimuth angle and elevation are averaged and presented in Figs.8 and 9,respectively.Figure 8 shows the variation of GRSS anomalies about its azimuthal mean on 15 January and 15 July 2003,with azimuth at a slope of 10◦,for these four mountainous ranges.The effect of the azimuth in winter is larger than that in summer.In January,the radiation anomalies over the southern slope are greater than 0,so the south side surface receives more solar radiation than the north side.This is due to the fact that the sunshine duration over the southern slope is much longer than over the northern slope.In July,the changes in radiation with azimuth are small,mainly because the difference in sunshine duration between the southern and northern slopes is small.Another apparent feature is that,over the southern slope(180◦),the GRSS at Tianshan is larger than that at Nanling in July.The reverse is true over the northern slope(0◦).This is due to the effect of latitude and astronomical factors.The variation of GRSS with latitude without the influence of the atmosphere depends on declination,slope angle and azimuth angle.On 15 January and 15 July,with a slope angle of 10◦,GRSS increases with an increase in latitude over the southern slope,whereas it decreases with an increase in latitude over the northern slope.Furthermore,the rate of increase in July over the southern slope is larger than that in January.Therefore,the difference in GRSS between Tianshan and Nanling is greater in July than in January.

Figure 9 shows the change in GRSS with height for the four mountainous areas.The GRSS increases with altitude,and this is due to two factors.Thefirst is that the extinction of solar radiation is reduced because the atmosphere becomes thinner as altitude increases;and the second is that with an increase in elevation over the southern slope,the sunshine duration increases.

7.Distribution of clear-sky daily GRSS in China

In this section,we analyze the geographic distribution of clear-sky daily GRSS in China.Figure 10 shows the results on 15 January and 15 July 2003 for the northern and southern slopes at a slope angle of 10◦.In January,it can be seen that the GRSS tends to distribute zonally,with large values at low latitudes and small values at high latitudes.The values over the southern slopes are clearly greater than those over the northern slopes.The white areas in each panel represent the opposite slope,i.e.the southern slope in the left-hand panels and northern slope in the right-hand panels.In July,the GRSS distribution is rather uniform,except over the Ti-betan Plateau where the GRSS values are greater than those in other regions.

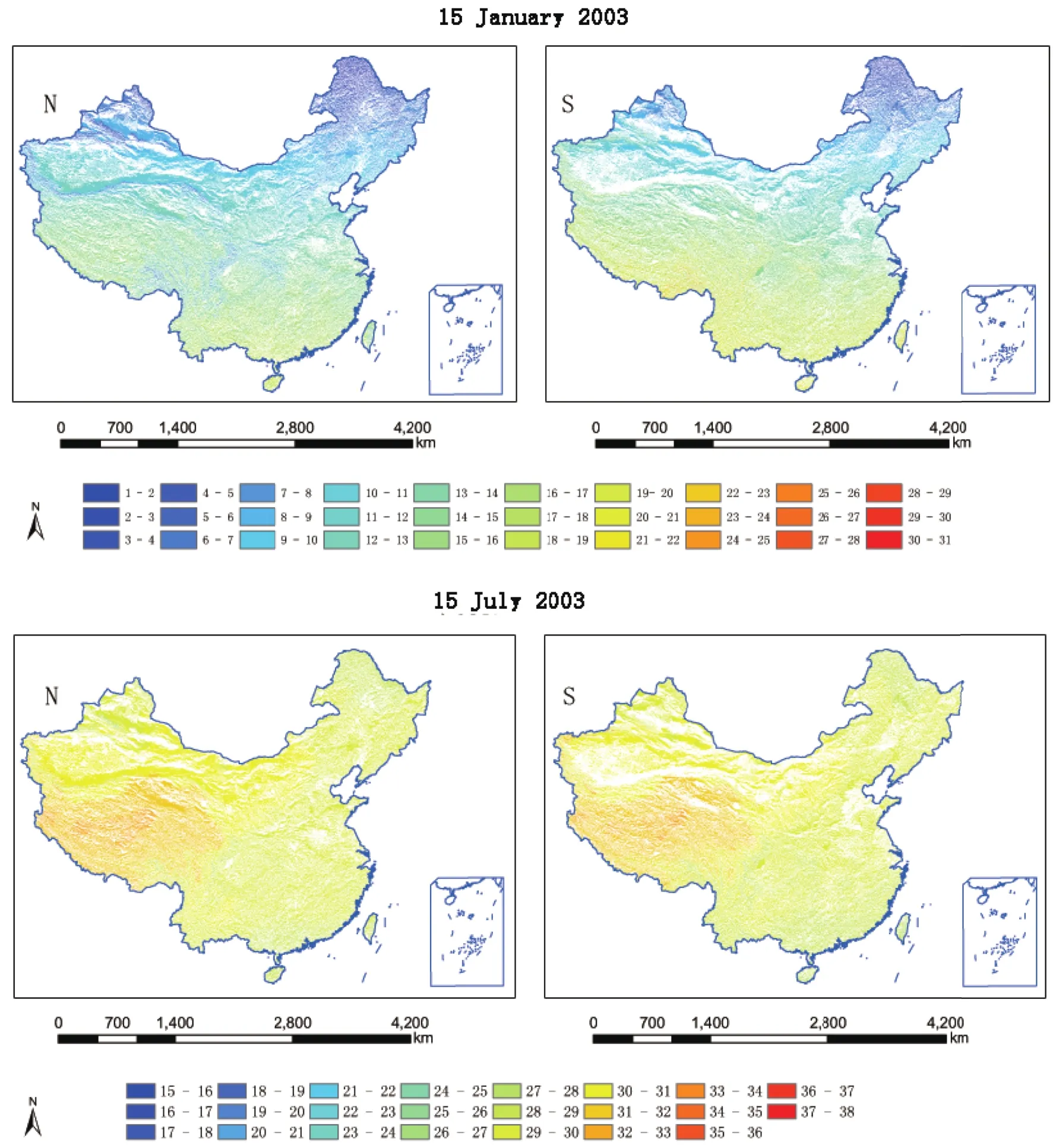
Fig.10.Distribution of clear-sky daily GRSS on 15 January 2003(top)and 15 July 2003(bottom)for northern(left)and southern(right)slopes at a slope angle of 10◦.

8.Conclusions

A new model to estimate daily global solar radiation over sloped topography in China is described in this paper.It is based on the Iqbal model C for estimating clear-sky radiation,the MODIS cloud fraction for considering the effects of cloud,and a DEM for implementing the effects of topography.The model is evaluated using observations at 98 radiation stations for both clear-sky and all-sky conditions.The results indicate that the model can be used to produce a reasonably accurate estimation of daily global solar radiation.

Based on the model calculations,the distribution characteristics of the GRSS associated with topographical factors are analyzed.The results can be summarized as follows:

The simulated GRSS distribution in all-sky conditions is very similar to that of the percentage of sunshine duration.Since the evaluation results for all-sky conditions confirm the accuracy of the method,it implies that the percentage of sunshine duration is still a good variable to represent the effect of cloud on the daily time scale.

Simulated results reflect well the effects of local topography(slope,aspect,degree of terrain shading)on solar radiation.The effect of azimuth in winter is larger than that in summer.The GRSS values are greater over southern slopes than over northern slopes.In summer,the GRSS over south-ern slopes increases with an increase in latitude.The reverse variation occurs over northern slopes.Similar changes also occur in winter,but the magnitude of the changes is much smaller and the effects may be insignificant.The change in GRSS with azimuth is greater in winter than in summer.GRSS also increases with an increase in altitude.

Finally,it is worth emphasizing that our model has the advantage that it only requires a few parameters(temperature,relative humidity,pressure,sunshine duration or total cloud fraction)as inputs,which are easy to obtain.It also has high spatial and temporal resolution,and therefore can be used to produce accurate high-resolation estimates of GRSS for smaller domains.This feature may be particularly useful for climate applications and agricultural planning for mountainous regions.

Acknowledgements.Prof.Rui SUN from Beijing Normal University is thanked for providing the surface albedo data.Dr.Zhian SUN and Dr.Michael NANGHTON from the Research&Development Branch,Australian Bureau of Meteorology,as well as the anonymous reviewers made many valuable comments and suggestions that led to improvements in the quality of this paper.

APPENDIX

A1.Direct irradiance for clean,wet air-Ib

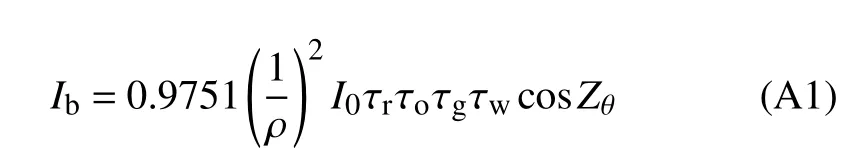
where(1/ρ)2is the sun–earth distance correction factor,I0is the solar constant(0.082 MJ m−2min−1),τris the transmittance of Rayleigh scattering,τois the transmittance of ozone,τgis the transmittance of uniformly mixed gases,τwis the transmittance of water vapor,and Zθis the zenith angle.

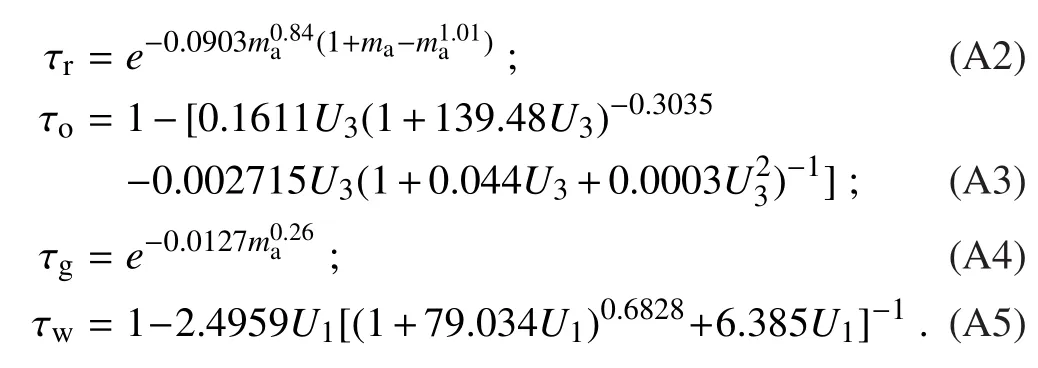
Here,ma=mr(p/1013.25)is the optical mass of air under actual conditions,p is the atmospheric pressure(hPa),and mris the optical mass for air under standard conditions,which can be determined using the following equation(Kasten and Young,1989):

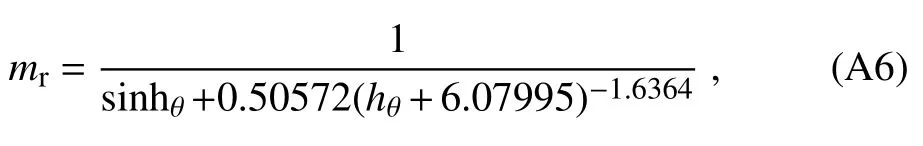
where hθis the solar altitude.

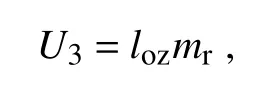
where U3is the ozone relative optical path length(cm)and lozis the vertical ozone layer thickness(cm),which can be determined using the methods of Van Heuklon(1979)and Manabe and Strickler(1964).

whereU1is the pressure-correctedrelativeoptical pathlength of precipitable water and w is the precipitable water,which can be determined by the following equation Leckner(1978):

where Hris the relative humidity and T is the temperature.

A2.Diffuse irradiance and Global irradiance Diffuse irradiance

This term is composed of two parts:the broadband diffuse radiation on the ground due to Rayleigh scattering(Dr),and the downward radiation due to multiple reflections between the ground and the atmosphere(Dm):

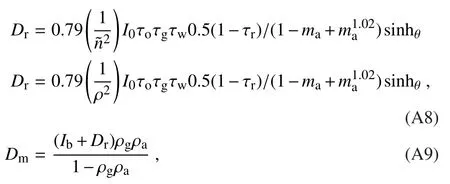
where ρgis the surface albedo and ρais the atmospheric albedo under clear-sky conditions.A constant value ρa(=0.0685)is assumed in this model:

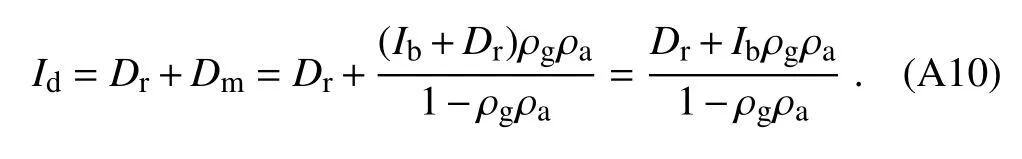
Global irradiance

Global irradiance is the sum of direct irradiance and diffuse irradiance:

A3.Daily global radiation overflat terrain under clear-sky

We obtain the daily global radiation under clear-sky conditions by

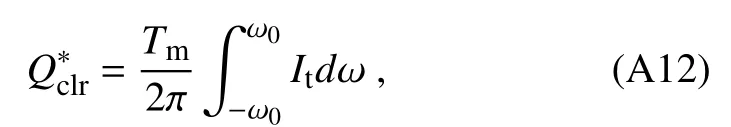
where ω0is the solar hour angle at sunrise and sunset,and Tmis the day length.

Because theformula of Itis too complicated,Eq.(A12)cannot be integrated analytically.It has to be obtained by numerical integration,which is conducted as follows:

(1)Given a time step length Tm(in minutes),the corresponding sun hour angle step length ω(in radians)is calculated by

∆ω is used as a time step length to divide the interval[−ω0,ω0]into n sub-intervals:

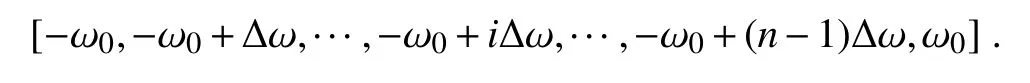
(2)The daily global radiation is determined by the summation of each interval:

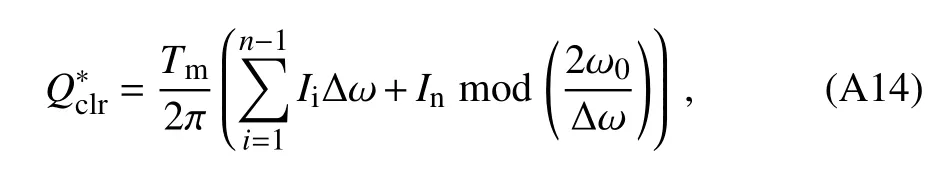
where Iiis the global radiation in each interval,Inis the global radiation at the last interval,and mod is the function used to obtain the remainder.

Bocquet,G.,1984:Method of study and cartography of the potential sunny periods in mountainous areas.Journal of Climatology,4,587–596,https://doi.org/10.1002/joc.3370040603.

Dozier,J.,and J.Frew,1990:Rapid calculation of terrain parameters for radiation modeling from digital elevation data.IEEE Transactions on Geoscience and Remote Sensing,28,963–969,https://doi.org/10.1109/36.58986.

He,H.L.,G.R.Yu,and D.Niu,2003:Method of global solar radiation calculation on complex territories.Resources Science,25,78–85,https://doi.org/10.3321/j.issn:1007-7588.2003.01.013.(in Chinese with English abstract)

He,Y.J.,X.F.Qiu,Y.Cao,and Y.Zeng,2014:Estimation of monthlyaveragesunshine duration overChinabased oncloud fraction from MODIS satellite data.Current Science,107,2013–2018.

Iqbal,M.,1983:An Introduction to Solar Radiation.Academic Press,Toronto,390 pp.

Kasten,F.,and A.T.Young,1989:Revised optical air mass tables and approximation formula.Applied Optics,28,4735–4738,https://doi.org/10.1364/AO.28.004735.

Leckner,B.,1978:The spectral distribution of solar radiation at the earth’s surface-elements of a model.Solar Energy,20,143–150,https://doi.org/10.1016/0038-092X(78)90187-1.

Li,J.,and X.Li,2007:Estimating solar radiation on slope using DEM.Acta Energiae Solaris Sinica,28,905–911,https://doi.org/10.3321/j.issn:0254-0096.2007.08.019.(in Chinese with English abstract)

Li,X.,G.D.Chen,X.Z.Chen,and L.Lu,1999:Modification of solar radiation model over rugged terrain.Chinese Science Bulletin,44,1345–1349,https://doi.org/10.1007/BF02885977.

Manabe,S.,and R.F.Strickler,1964:Thermal equilibrium of the atmosphere with a convective adjustment.J.Atmos.Sci.,21,361–385,https://doi.org/10.1175/1520-0469(1964)021<0361:TEOTAW>2.0.CO;2.

Manners,J.,S.B.Vosper,and N.Roberts,2012:Radiative transfer over resolved topographic features for high-resolution weather prediction.Quart.J.Roy.Meteor.Soc.,138,720–733,https://doi.org/10.1002/qj.956.

Platnick,S.,S.A.Ackerman,M.D.King,K.Meyer,W.P.Menzel,R.E.Holz,B.A.Baum,and P.Yang,2015:MODIS atmosphere L2 cloud product(06L2).NASA MODIS Adaptive Processing System,Goddard Space Flight Center.

Qiu,X.F.,Y.Zeng,and S.M.Liu,2005:Distributed modeling of extraterrestrial solar radiation over rugged terrain.Chinese Journal of Geophysics,48,1100–1107,https://doi.org/10.1002/cjg2.753.

Qiu,X.F.,Y.Zeng,Y.J.He,and C.M.Liu,2008:Distributed modeling of diffuse solar radiation over rugged terrain of the YellowRiverBasin.ChineseJournalof Geophysics,51,700–708,https://doi.org/10.1002/cjg2.1262.

Shi,G.P.,X.F.Qiu,Y.Zeng,and Y.P.Qiu,2013:Remote sensing integration model of sunshine percentage based on cloud cover images.Journal of Remote Sensing,17,1508–1517,https://doi.org/10.11834/jrs.20133032.(in Chinese with English abstract)

Tian,Y.Q.,R.J.Davies-Colley,P.Gong,and B.W.Thorrold,2001:Estimating solar radiation on slopes of arbitrary aspect.Agricultural and Forest Meteorology,109,67–74,https://doi.org/10.1016/S0168-1923(01)00245-3.

Valiente,J.A.,M.Nunez,E.Lopez-Baeza,and J.F.Moreno,1995:Narrow-band to broad-band conversion for Meteosatvisiible channel and broad-band albedo using both AVHRR-1 and-2 channels.Int.J.Remote Sens.,16(6),1147–1166,https://doi.org/10.1080/01431169508954468.

Van Heuklon,T.K.,1979:Estimating atmospheric ozone for solar radiation models.Solar Energy,22,63–68,https://doi.org/10.1016/0038-092X(79)90060-4.

Wang,K.C.,X.J.Zhou,and J.M.Liu,2004:The effects of complex terrain on the computed surface solar short-wave radiation.Chinese Journal of Atmospheric Sciences,28,625–633,https://doi.org/10.3878/j.issn.1006-9895.2004.04.14.(in Chinese with English abstract)

Weng,D.M.,1964:Discussion on climatological calculation method of solar radiation.Acta Meteorologica Sinica,34,304–315,https://doi.org/10.11676/qxxb1964.032.(in Chinese with English abstract)

Williams,L.D.,R.G.Barry,and J.T.Andrews,1972:Application of computed global radiation for areas of high relief.J.Appl.Meteor.,11,526–533,https://doi.org/10.1175/1520-0450(1972)011<0526:AOCGRF>2.0.CO;2.

Yeom,J.M.,Y.K.Seo,D.S.Kim,and K.S.Han,2016:Solar radiation received by slopes using COMS imagery,a physicallybasedradiationmodel,andGLOBE.Journalof Sensors,2016,4834579,https://doi.org/10.1155/2016/4834579.