顾及近景图像特征点误差各向异性的三维空间重构

梁 艳

(江苏海事职业技术学院，江苏 南京 211170)

随着人们对数字城市建设的关注程度越来越高，全面、真实、准确地获取地理空间数据并再现三维空间结构已经成为虚拟地理环境的核心研究问题之一[1]。在地理数据中，三维点云已经成为三维空间信息的重要数据源，在数字城市、虚拟现实、古建筑重建、公安侦探、工业制造等诸多领域中都发挥着重要的作用[2]。目前，三维点云的获取方式有多种，可采用激光扫描、雷达、数字摄影方式等[3]，其中，基于近景图像序列的三维点云采集方法，因其具有成本低、效率高、劳动强度低等特点，已成为一种吸引众多领域日益关注和采用的空间信息获取的有力工具[4]。

在三维点位置的计算过程中，描述像片位置和姿态的像片内外方位元素的精确解算是实现目标三维空间重构的必要前提[5]。因此，如何准确计算像片内外方位元素并进一步解算三维空间点位置是恢复三维空间结构的核心和关键。Heyden、Pollefeys、Snavely等利用较具代表性的SFM(Structure from Motion)方法实现了像片方位元素的计算[6，7]，该方法利用光束法平差，先构造误差方程，从图像EXIF信息中提取焦距、CCD宽度等参数作为像片方位元素的初始参数，迭代计算并同步得到像片的内外方位元素及三维空间点位置，该方法避免传统方法中将像片的方位元素和三维空间点位置分布解算的误差传播及过程繁琐问题，将计算过程简化[8,9，10]。

近景图像序列由于多采用大交角大重叠的摄影方式，会引起更大、更复杂的几何变形，用于重构三维空间的图像特征点邻域也存在较大的畸变[11]，导致特征点处的定位误差通常是各向异性，而且常常具有很强的方向性[12]。然而，当前SFM方法并未考虑图像特征点处的畸变程度及其引起的误差的分布方向问题，显然该方法所得到的解并不能很好地适应近景图像透视畸变较大引起的误差各向异性等实际应用情况。

针对近景图像特征点畸变较大问题，本文探讨一种顾及近景图像特征点误差分布各向异性的三维空间重构方法。

1 基于SFM方法的三维重构原理

1.1 运动恢复结构流程

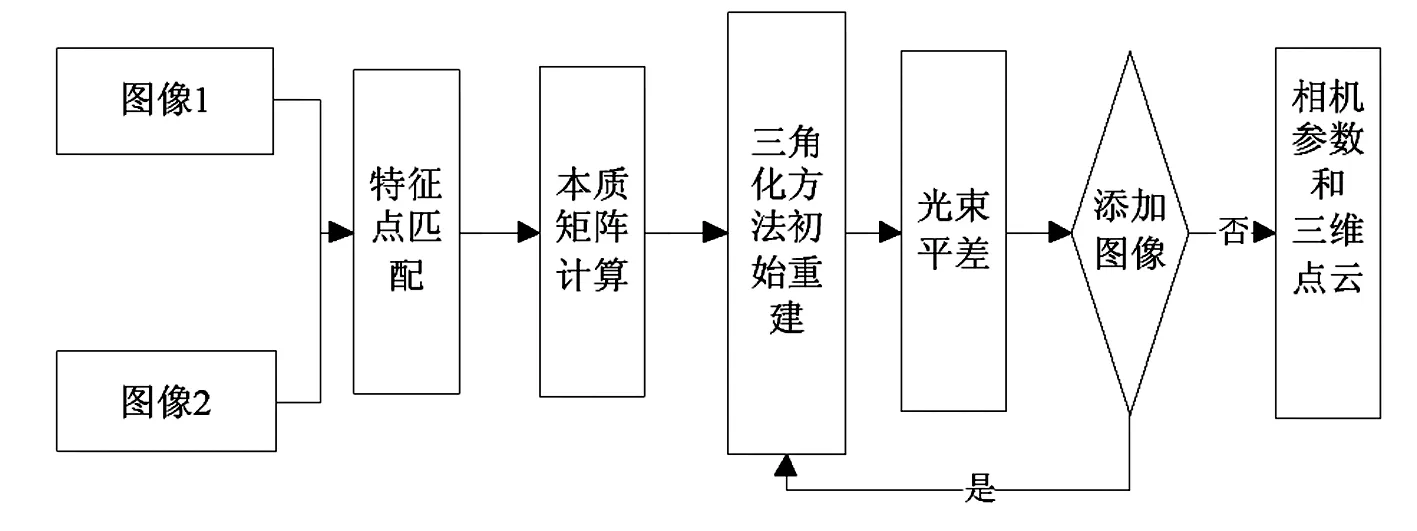
图1 运动恢复结构方法流程

在运动恢复结构方法中，光束平差贯穿于整个三维信息解算过程的始终，如图1所示，首先利用特征点提取及匹配得到表征特征之间对应关系的本质矩阵，利用三角化方法进行初始结构重建，得到两图像的初始内外方位元素及三维空间点位置，然后对初始值进行光束法平差优化；对每幅新添加的图像，求解新增图像的内外方位元素及未被解算的匹配特征点对，并进行光束法平差优化；在局部光束平差优化的基础上，最后做全局优化，得到所有图像的方位元素与三维点特征的最优解[13]。

1.2 光束平差优化模型

共线方程表示像点、摄影中心及空间点之间关系[14]，简单描述为：m=f(X,P)。其中，m为像点位置，X为相应的目标空间点位置，P为投影矩阵，分解后可得到像片的内外方位元素。

光束平差以共线方程作为基本的数学模型，将像点坐标作为观测值，通过最小化反投影误差构建误差方程[11]：

在误差方程中，Vi表示三维空间点Xi与图像中特征点的相对应关系，即表示Xi在哪些图像中可以被“看”到。

光束平差法采用非线性最小化算法来迭代解算误差方程，对当每一像点误差小于某一限差时，迭代计算结束。通过此计算过程中，三维点云结构和像片的内外方位元素得到优化。

2 近景图像特征点的误差各向异性

2.1 仿射变换

近距离拍摄的图像，一般存在较大的透视畸变或几何变形，对于在近距离、不同视点下获取的近景图像，对应的局部区域之间的关系可以利用仿射变换矩阵表征[11]。

同一图像中不同特征点邻域的灰度信息以及同名点邻域灰度模式在不同图像上均不相同。仿射变换下局部邻域属性相对稳定的特征点，即仿射不变特征点，仿射变换矩阵可以借助仿射不变特征局部区域的匹配进一步求解。

2.2 特征点分布各向异性

图2为3种不同程度的仿射变换，仿射不变特征点的局部区域采用椭圆来描述，表示两幅图像对应的椭圆内部整体灰度信息基本相同，不受仿射变换的影响，椭圆的长、短轴方向及长度分别表示该特征点所在位置即椭圆圆心处定位误差分布的不确定性的方向和大小。从图中可以看出，特征点只有在正交角点时，误差分布的不确定性在水平和垂直方向上大小相等且相对较小，当特征点为锐角或钝角角点时，误差分布的不确定性在水平和垂直两个方向上大小上并不相等[12]。

图2 特征点误差分布

传统光束平差模型中，误差方程的构建并未考虑误差分布的不确定性在水平和垂直两个方向上大小上并不相等时的情况，它仅以误差分布各向同性即情况(a)为假设前提，那么按照传统方法求解的相机参数及三维结构并不能与(b)和(c)相适应。

为进一步提高三维结构计算的精度，结合误差分布特点，解算三维结构信息时应考虑特征点的畸变程度，构建符合近景图像本身实际情况的新的光束平差优化模型。

3 顾及误差各向异性的三维空间重构

本文利用图像之间的仿射变换原理，将误差的各向异性产生的影响和作用融入到光束平差优化模型中，并构造相应的误差方程，使得即使在特征点误差分布的不确定性是各向异性时，最小化误差方程所得到的解也是最优解。

由于特征点仿射不变区域的不同，对解的约束作用及贡献也应该是不同的。如何体现各个特征点误差分布的各向异性对三维结构解的作用是解算的关键，根据文献[15]的原理，利用特征点的协方差矩阵构造仿射变换矩阵，通过该仿射变换矩阵将图像上原始二维特征点和计算的三维点在图像上的重投影点变换到统一的仿射不变区域空间中，通过此变换使得特征点的误差分布由各向异性分布映射到各向同性的空间中，如图3所示。

图3 误差分布映射过程

用特征点的二阶矩矩阵Q可以计算误差椭圆表示的局部各向异性结构的形状，将Q做奇异值分解：

Q=U∑UT

Q-1=U∑-1UT

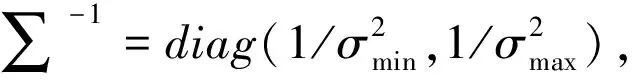
利用变换后的点坐标数据可以构造出体现误差分布各向异性的、更具统计意义的反投影误差，定义如下：

可以看出，对各个特征点的反投影误差利用仿射变换矩阵进行了加权处理，将仿射变换矩阵的系数分配到误差方程的相应系数上后，新的误差方程重新定义如下[10]：

当所有二维特征点及反投影点经过加权处理后，误差的各向异性得以体现，每个特征点的误差不确定性对误差方程作出不同的贡献，即特征点的不确定性越大，对误差方程的贡献就要越小，特征点的不确定性越小，对误差方程的贡献就要越大。

利用上述方法构造的新误差方程，采用非线性算法来最小化加权反投影误差的平方和，最终可实现三维点云结构和相机参数的优化。

4 实验结果与分析

4.1 实验设计

为了验证本文方法的有效性，以从不同视角真实拍摄的不同大小、可变焦距的南京师范大学图像序列以及加利福尼亚大学公开的瓦勒堡建筑图像序列进行实验，图4显示了图像序列中的部分图像。

图4 图像序列

对以上图像序列，分别利用本文考虑特征点误差各向异性的三维空间重构方法与传统方法进行实验。为进行对比分析，评价精度的度量方式采用所有重构空间点在图像平面上的平均反投影误差εr表示(单位：像素)[16]，由下式给出：

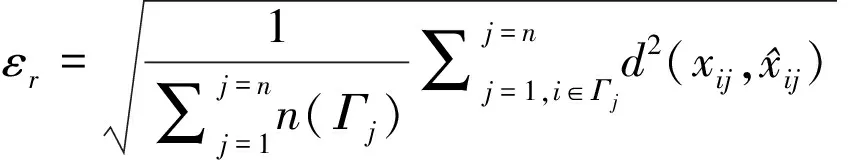
4.2 实验结果

图5显示了利用本文方法计算的三维空间点位置。

图5 本文方法恢复的三维空间稀疏点云

传统光束平差方法与本文方法比较结果如表1所示。

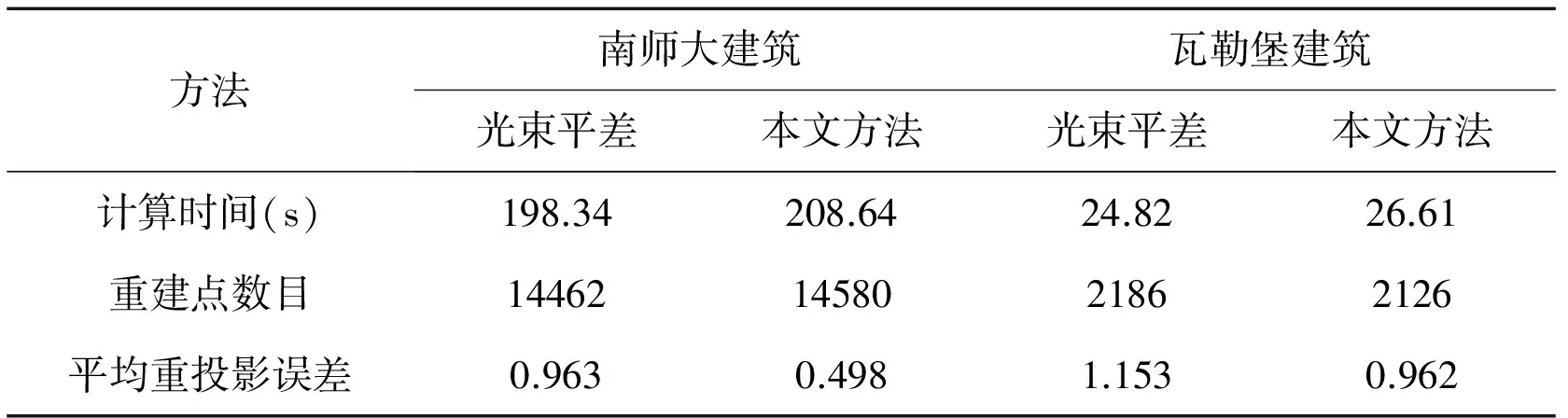
表1 传统光束平差与本文方法解算结构对比

4.3 实验分析

从实验结果看出，本文方法由于增加了特征点误差各向异性的转换及相关计算，计算时间比传统光束法平差方法略长，但对整个过程影响不大。在同一阈值控制范围内，两种方法重构的点云数量相当；从计算精度分析，本文方法的计算精度提高，其原因主要是传统方法并没有考虑特征点误差的各向异性分布问题，本文方法的平均反投影误差基本控制在一个像素左右，明显低于传统方法。

值得注意的是，本文方法可以有效解算出三维空间点坐标，但仅依靠SFM方法中特征点提取及匹配解算出的点云较稀疏，要想重构真实三维模型，还需要进一步借助图像的稠密匹配或其他方法辅助完成。

5 结语

在运动恢复结构的技术框架下，本文探讨了一种考虑近景图像特征畸变的三维空间重构的方法，在分析了特征点误差不确定性分布特点的基础上，利用特征点协方差矩阵构造仿射矩阵对特征点坐标进行变换，并对误差方程进行不确定性系数加权，构造新的光束法平差优化模型，使其适应于不同程度的近景图像特征畸变情况，通过迭代计算得出三维空间点坐标的最优解。最后通过实验验证，与未考虑特征点误差各向异性的传统方法相比，本文方法计算精度有了明显提高。

[1] 王波.影像特征线辅助下的三维激光点云建筑物建模[D].南京师范大学，2013.

[2] 宋宏权，刘学军，闾国年，等.地理参考下未标定图像序列的三维点云精度分析[J].测绘通报，2012,(7)：14-16.

[3] 陈红权，郭威.三维激光扫描技术在桥梁形变监测中的应用[J].现代测绘，2016，39(1)：36-39.

[4] 盛业华, 张卡, 叶春, 等.基于灰度投影的数字近景摄影立体影像匹配[J].光学学报, 2005, 25(12): 1623-1628.

[5] 王佩军，徐亚明.摄影测量学[M].武汉大学出版社，2010.

[6] FAUGERAS O D.What can be seen in three dimensions with an uncalibrated stereo image?[C].Springer Berlin Heidelberg on Computer Vision-ECCV’92, 1992,563-578.

[7] SNAVELY N, SEITZ S M, SZELISKIi R.Photo tourism: exploring photo collections in 3D[J].ACM transactions on graphics (TOG), 2006, 25(3): 835-846.

[8] TRIGGS B, MCLAUCHLAN P, HARTLEY R I.Bundle adjustment-a modern synthesis[C].Springer Berlin Heidelberg on Proceedings of the International workshop on Vison Algorithms, 2000: 298-372.

[9] TRIGGS W, MCLAUCHLAN P F, HARTLEY R I, et al.Bundle adjustment for structure from motion[J].Vision Algorthms:Theory and Practice.Springer Verlag, 2000.

[10] 詹总谦,张祖勋,张剑清.基于稀疏矩阵技术的光束平差快速算法设计[J].测绘通报,2006, 12:5-8.

[11] 梁艳,盛业华,杨林，等.大交角近景影像的仿射不变特征匹配方法研究[J].测绘科学，2013，38(3)，98-100.

[12] 苗锡奎，朱枫，郝颖明，等.基于特征点不确定性加权误差的位姿估计新方法[J].光电子.激光，2012，23(7):1348-1355.

[13] 胡建才，刘先勇.基于因子分解和光束法平差的摄像机自标定[J].光电工程，2011,38(3):63-66.

[14] 王成亮.基于近景图像序列的建筑物三维模型重建研究[D].中南大学，2009.

[15] STEELE R M, JAYNES C.Feature uncertainty arising from covariant image noise[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005,1: 1063-1070.

[16] 甄艳.序列视频稠密点云恢复关键技术研究[D].南京师范大学，2013.