轨道安全监测中传感器优化配置研究

2018-01-26刘超

铁道标准设计 2018年3期

刘超

(中铁第一勘察设计院集团有限公司,西安 710043)

随着城市建设加快，地铁、市域铁路作为城市交通大动脉，扮演着越来越重要的角色。然而，客运量增加、列车往返碾压和复杂运营条件的不间断作用，使轨道结构不可避免地出现疲劳损耗和局部破损。这些隐患不会立即破坏整体系统，但对整个结构的安全已构成潜在威胁，隐患不断累积会导致局部破损愈演愈烈，轻则影响线路状态劣化乘车体验，重则造成脱轨，车毁人亡[1]。目前对于轨道系统的监测一般采用夜间天窗点人工上道巡检和周期性车载检测[2]，无法实时掌控轨道状态，所以结构安全监测意义重大，也是未来轨道结构安全评估的重点环节。

对于轨道监测系统，传感器布置的越多，得到的监测数据就越详细，从而更有利于分析轨道结构的服役状态。但实际情况中，综合考虑经济性、线路运营安全性等因素，钢轨监测测点无法达到较高密度，监测时传感器间距远大于期望值，所以在进行传感器布置时，如何选择测点位置、安装间距，如何保证监测的准确性、经济性一直是困扰和制约轨道交通行业结构长期安全监测技术发展的难题。

国内很多学者对轨道结构的监测技术进行了研究，但主要都集中于高速铁路[3-5]；除此之外，轨道结构监测中传感器监测位置的选择和监测方案的评价方法还没有形成体系[6-10]。因此，如何将有限的传感器配置在最优位置，通过Ω区域内布置的n个传感器达到技术和经济的最优组合，发展科学、经济和合理的轨道结构安全监测技术是当前的研究重点[11]。

1 优化准则

目前用于传感器测点方案优化的常用方法有：模态动能法(MKE)、有效独立法(EI)、遗传算法(GA)；常用的优化准则有传递误差最小准则、插值拟合准则和模态应变能准则等[12]。轨道系统是长条带状结构，在车辆、温度、基础变形等荷载的组合作用下受到剪力、温度力、附加力等力的作用，无法用一个表达式来进行全面描述，因此可以采取插值拟合误差最小准则针对不同类型监测指标来配置传感器。

传感器监测数据是以一种离散点的形式来呈现的数据结果，将这些离散点连起来会形成一条由多线段组成的连续折线。当测点足够多时，多测点组成的测点折线和钢轨受力曲线便可达到高拟合状态，这样的测试结果真实可信，监测效果也可达到最好状态。

为了分析传感器的位置、数量及拟合方法的精度，可利用结构分析软件(如ANSYS或其他结构计算软件)计算出额定荷载作用下结构的实际效应值，再通过调整传感器布置位置得到输出值拟合效应曲线，最后根据误差最小准则，在满足经济性前提下得到传感器布置方案[14-15]。

2 数学模型

采用插值误差最小准则配置传感器的数学模型为：设目标值由直接测量的钢轨参数x1，x2，…，xn决定,δ1，δ2，…，δn分别为其误差，Δy代表由δ1,δ2，…，δn引起的误差，则有

y+Δy=f(x1+δ1,x2+δ2,…,xn+δn)

(1)

将(1)式按泰勒级数展开，并略去高阶无穷小，得

(2)

那么最大误差为

由上述算式可知，传感器最优方案的选择，不仅仅是数目n的选择，还包括给定区域上的位置选择[12]。

选定一种传感器的布置方式，即当区域和数量n给定时，存在一个Δymax，按照误差最小准则，传感器布置的最优目标为

min(Ω,n)=(Δymax)

(3)

3 测点方案优化体系

3.1 测点选择

轨道结构的受力是影响其强度和稳定性的主要因素，也是无缝线路检算的重要指标。钢轨应力的监测数据可以直接反映出结构的受力情况，从而判断出安全服役状态[13]。而在所有轨道结构中，桥上渡线道岔承受复杂的运行荷载和环境作用，具有最特殊的力学特性。以12号渡线道岔为例对测点优化进行研究，并建立精细化空间耦合模型。12号渡线道岔及建立的ANSYS模型如图1所示。

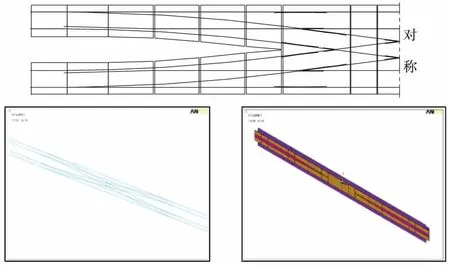
图1 12号渡线道岔及空间模型

根据道岔敏感区域的初步分析结果可知，道岔钢轨的最大纵向力出现在基本轨上，因此选择桥上渡线道岔基本轨纵向力为研究对象进行测点布置和优化研究。由模型分析得到的直基本轨纵向力如图2所示。

图2 离散测点纵向力

在基本轨上布置传感器，即通过布点使传感器得到的纵向力来描述道岔受力曲线，监测纵向力的同时得到钢轨的受力状态。在选择传感器位置时利用曲线斜率的变化量(二阶倒数)作为评价数据间相关性的指标。图2中相邻两点QiQi+1{(xi，yi)，(xi+1，yi+1)}的斜率为ki，随后相邻数据长度两点Qi+1Qi+2{(xi+1，yi+1)，(xi+2，yi+2)}的斜率为ki+1，两个斜率之差的绝对值|Δk|可用来描述点Qi+1对于曲线的贡献值。贡献值越大，认为它对描述曲线线型具有更明显的作用。

在布设测点时即可选择曲线贡献值所对应较高的测点。如图3所示，k1，k2两点的贡献值最大，当钢轨纵向力如图中所示曲线时，测点只用布置端点、k1、k2四个即可，4个测点数据所连曲线与原曲线拟合度最高，误差最小，传感器布置目标达到最优。

图3 曲线贡献值

通过Matlab将钢轨坐标和对应纵向力数据输入，可自动计算出对应钢轨坐标的曲线贡献值，部分钢轨单元贡献值如表1所示，绘制三维图表如图4所示。其中X轴表示钢轨位置坐标，Y轴表示对应单元的纵向力，Z轴为曲线贡献值。从图4中可知，曲线拐角处Z轴数据明显变高，说明曲线在此处斜率的变化量明显增大，是曲线高贡献值点。在曲线比较圆滑的地段Z轴高度趋近于零，曲线斜率变化较为缓慢，纵向力变化较为频繁地段Z轴高度呈现锯齿形波动变化，说明此处纵向力需要进行连续监测，同时也对敏感区域、敏感点寻找方法进行了验证。在进行测点布置时，按照敏感区域范围内钢轨单元个数，每次选择1%的数组进行绘图。12号桥上渡线道岔直基本轨包含347个钢轨单元，每次增加4个测量单元。选择测量单元坐标时按照贡献值由大到小依次选取。选取测点位置后再与起点、端点坐标数组依次连接构成传感器监测布设曲线。分步次排列的测点曲线如图5所示。

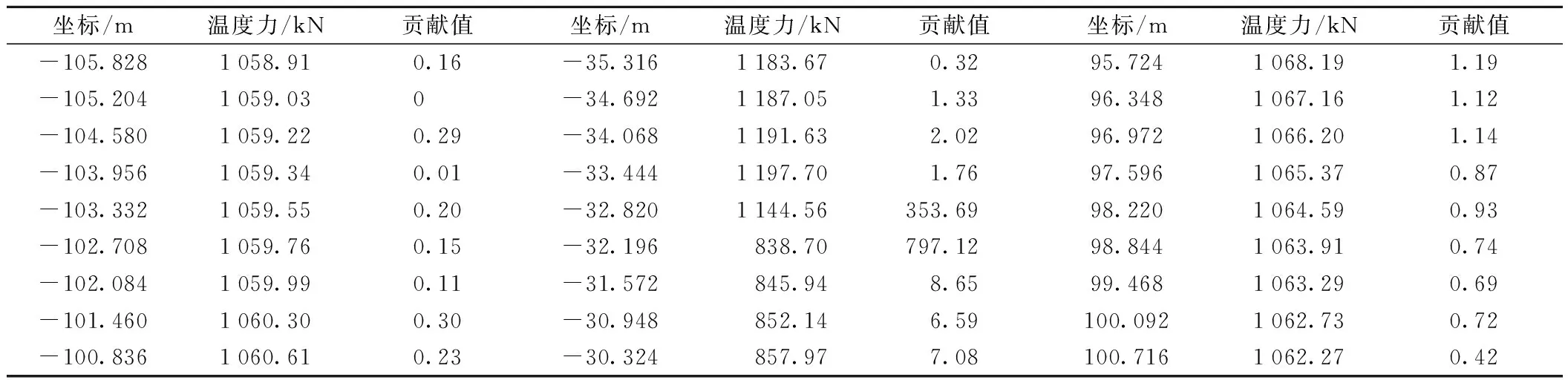
表1 钢轨纵向力测量单元贡献值(部分)

图4 钢轨单元和对应纵向力和曲线贡献值

从图5可知，在第4次选择位置后绘制的测点曲线已经能够极好地描述钢轨纵向力的线型。第3次选择位置后绘制的测点曲线可基本满足长期监测需求，第1、2次选择位置后绘制的测点曲线不能保证监测的准确性。

3.2 方案选择

按照误差最小准则，由传感器测得的钢轨纵向力与刚度、应变量的关系式：f(x)=EIε(x)，可得到测点优化布置的目标函数

(4)

式中，EI为刚度；ε为传感器测得的应变量；f(x)为钢轨纵向力；(Ω,n)为最优传感器布置方案。

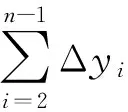
继续进行6次测点选取，求得误差比率后做散点图并进行线性拟合，结果如图6(a)所示。拟合曲线Adj. R-Square=0.987 75，表明具有极高精确度。

当所有钢轨单元都被布置传感器时，误差比率趋近于零，此时的误差比率散点图和拟合曲线如图6(b)所示，其拟合曲线Adj. R-Square=0.987 75，拟合曲线公式相同。

图5 不同步次绘制的测点曲线

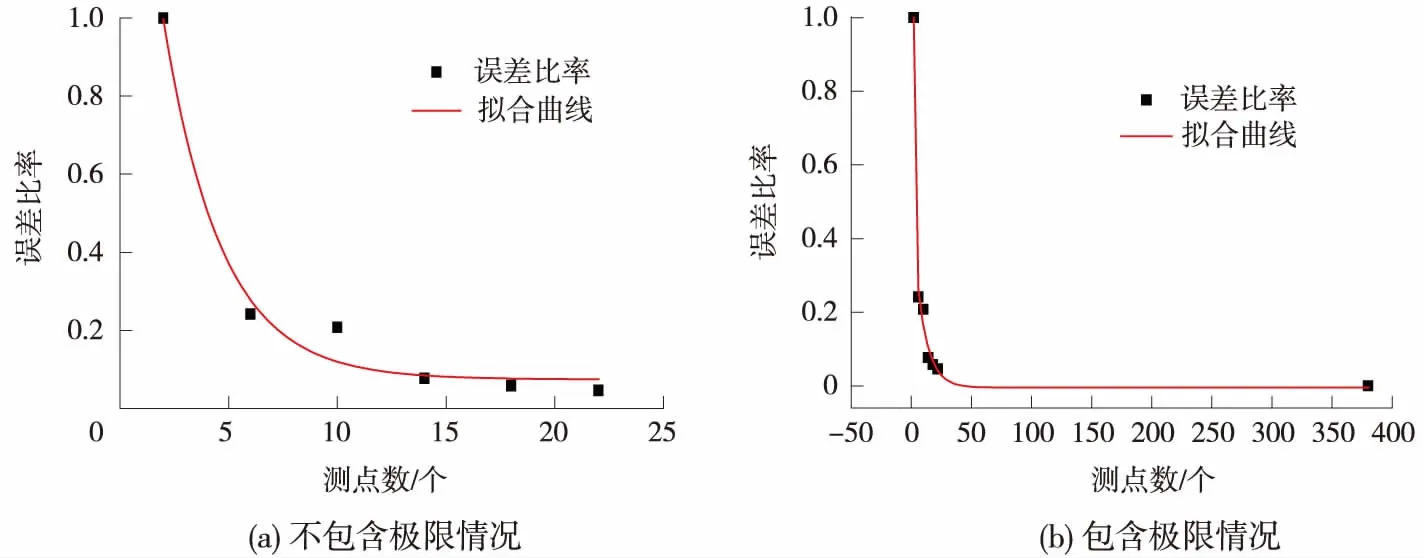
图6 误差比率散点

通过两次绘制的散点图和拟合曲线可以发现，随着测点个数的增加，误差比率以指数形式递减，即增加传感器个数后带来的测点准确性收益逐步减小。由图6(a)可知，第3次的误差比率已经达到较好状态，此数值在图6(b)中处于拐点底部。考虑安全富余量，选取0.08为误差比率限值(略小于第3次对应数值)，此时认为测点方案既满足了准确性，又保证了经济性。

以误差比率限值来看，第4次增加测点时形成的布置方案满足了安全评价标准。从图7可以看出，在部分区段内由于数值波动较大，设置的传感器个数较多，但纵向力数值相差不大。从经济性的角度出发，可考虑减少这些区域的传感器。图8为修改后的方案，新的方案删减了部分密集区域的传感器，此时误差比率为0.08，满足监测要求。

图7 修改前监测方案

图8和表2所示即为桥上渡线道岔直基本轨纵向力监测传感器布设方案。道岔结构其余部分敏感指标的传感器测点布置方案确定方式与钢轨纵向力指标相同，首先通过模型分析确定不同结构单元的受力数值，在此基础上通过贡献值的思路确定监测单元，最后通过基于误差最小准则原理优化监测方案，将误差控制在合理范围内，并保证经济合理性。