弧长比例对曲线斜拉桥力学性能影响分析
2018-01-26单德山汪子涵张二华
单德山,汪子涵,张二华
(西南交通大学土木工程学院,成都 610031)
斜拉桥是一种古老而又年轻的缆索承重系统,随着交通运输业的蓬勃发展,斜拉桥的建设得到了快速发展,其结构形式日新月异,跨越能力不断增大,大跨度斜拉桥桥梁结构已成为公路和铁路交通设施的重要组成部分[1-3]。较之普通梁式桥,斜拉桥跨越能力更强,而相比于悬索桥,其刚度更大,抗风能力更强[4]。随着桥梁建设技术与设计理念的不断发展,作为斜拉桥分支之一的曲线斜拉桥势必得以快速发展,其不仅可以很好地适应山区地形限制和路线线形要求,而且可以满足美观要求[5]。
曲线斜拉桥主梁曲率使得斜拉桥体系受力及空间结构变得更为复杂,兼具曲线梁桥和斜拉桥的受力性质[6]。结构几何关系方面:主梁由于处于缓和曲线与圆曲线上,其桥塔、拉索、主梁以及锚固点的坐标具有空间性;结构受力方面:在拉索沿曲线圆心方向存在径向的水平分力以及弯曲主梁重力作用下,主塔与主梁均处于复杂的空间受力状态,结构构件均承受空间的弯矩、剪力与扭矩的作用,而且面内弯矩、面外弯矩与扭矩相互耦合[7],本文简称为“弯-扭耦合”作用。而圆心角设计参数直接影响着主梁“弯-扭耦合”作用大小,是影响曲线斜拉桥结构体系受力状态的关键因素。
圆心角设计参数可分为两类:第一类为保持圆弧长度不变,改变主梁曲率半径;第二类为保持曲率半径不变,改变主梁圆弧长度。目前,国内学者对第二类圆心角设计参数(本文称为“弧长比例”参数)研究较少,主要针对第一类圆心角设计参数展开研究工作。
刘凯[8]基于有限元软件分别建立了曲线半径相同的单索面和双索面斜拉桥模型,通过改变曲率半径,研究了曲率半径变化对单、双索面斜拉桥结构静力、动力特性的影响,并通过对比分析,研究不同曲率半径下单、双索面体系对斜拉桥整体力学行为的影响;杨凯[9]以某曲线混凝土箱梁斜拉桥为实例,研究了不同曲率对主梁受力性能的影响:曲率半径的变化对竖向弯矩与轴力影响较小,对主梁的弯矩与扭矩影响很大;齐宏学[10]基于有限元软件建立了不同曲率半径的曲线混凝土箱梁斜拉桥模型,对计算结果进行对比分析得出:曲率半径变化对主梁弯矩、扭矩及主塔塔底弯矩影响较大,且随曲率半径增大而增大。以上研究均基于弧长不变,曲率半径变化进行的,而本文由于背景桥梁的特殊性(部分曲线斜拉桥,详见图1),针对第二类圆心角设计参数展开研究工作。
目前,有关大型复杂桥梁的结构分析多采用空间有限单元法进行计算,该法工作计算量小,能够借助现有有限元软件较为准确的模拟实际结构,并且对结构施工过程进行仿真分析,从而得到成桥状态,并通过大量实践得到验证,适于桥梁结构设计[11]。本文以不同弧长比例对曲线斜拉桥受力状态的影响为研究目标,通过Midas/Civil 2015有限元软件建立不同弧长比例的有限元模型,对计算结果进行详细的分析,掌握参数变化时斜拉桥结构受力性能变化的趋势,以确定更合理的结构形式[12,13],同时对同类型的桥梁设计提出相应建议。
1 工程背景及计算模型
以刚果布拉柴维尔滨河大道混凝土曲线斜拉桥为依托,进行建模分析。该桥全长545 m,为跨径布置49 m+81 m+285 m+81 m+49 m的双塔五跨双索面曲线形斜拉桥,结构采用半漂浮体系,即塔墩固结梁底放置纵向固定支座,此既能满足结构正常使用要求,又能提高结构地震下的安全性[14]。主梁布设双向四车道,曲线梁起始点为跨中,曲率半径为550 m。主梁为预应力混凝土Π形截面,主梁中心梁高2.3 m,桥宽22.0 m,顶面设置双向2.5%横坡。斜拉索采用扇形式布置,标准索距为9.0、6.0 m。索塔采用钻石造型,塔柱为钢筋混凝土构件,P2桥塔塔高122.2 m,P3塔高119.7 m。斜拉索编号及全桥概况如图1所示。

图1 全桥概况(单位:cm)
采用桥梁专用分析软件Midas/Civil 2015建立该桥梁的空间梁板混合模型,弧长比例为0.50的Midas/Civil有限元模型如图2所示。其中,主梁截面采用空间梁板单元组合进行模拟(即采用梁+板单元进行模拟,主梁顶板采用板单元模拟,两个梁肋采用梁单元模拟),该模拟完全按照主梁的实际组成来模拟,可以较为真实地反应结构的实际关系和质量分布[15],如图3所示;桥塔和桥墩采用梁单元模拟;支座采用弹性连接模拟;斜拉索采用索单元模拟。

图2 Midas模型示意
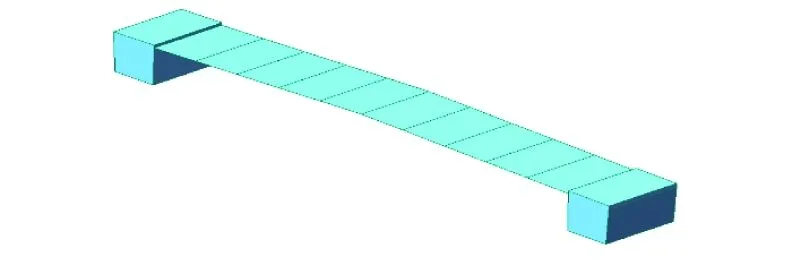
图3 Midas模型主梁断面
主梁纵向预应力钢束分为悬臂钢束、边跨现浇段钢束和合龙钢束3种,预应力钢束直径为15.20 mm,钢束设计锚下张拉控制应力为0.75fpk=1395 MPa,标准梁段预应力钢束布置见图4所示。在建模过程中,梁肋中的预应力作用按设计布置预应力钢束,而桥面板中的预应力作用采用等效荷载法[16]计算的等效集中力进行模拟,当梁中心线为曲线时,预应力等效如图5所示,由∑M=0,可得q=Fx/R,其中R为曲线曲率半径。

图4 梁段预应力钢束布置(单位:cm)
2 计算结果及分析
为了研究弧长比例变化对桥梁结构受力性能的影响,在背景桥梁的基础上,通过改变弧长比例,分别建立弧长比例为0.00、0.44、0.50、0.64、0.76、0.89、1.00的有限元模型,各工况见表1,主要分析弧长比例变化对曲线斜拉桥成桥阶段受力性能的影响。
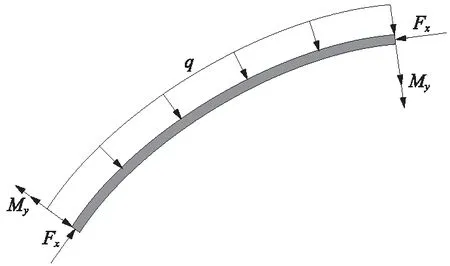
图5 曲线段板单元预应力等效图示

表1 弧长比例工况
2.1 主梁正应力结果分析
曲线斜拉桥由于索力作用和弯曲主梁重力的影响,主梁处于复杂的空间受力状态,弧长比例的改变直接影响着主梁空间受力状态,从而影响主梁各截面的应力分布,选取设计关心的截面正应力作为研究对象。成桥阶段主梁各截面极值正应力对比如图6所示。
由图6可知,在成桥阶段,当弧长比例由0.00变化到1.00时,主梁各截面极值正应力随弧长比例在不同区间变化呈现不同变化趋势,为更好分析这种变化趋势,选取两边跨2分点(CLS7截面、CRS7截面)、跨中附近(CLM15截面、CRM15截面)共4个主梁截面作为主要分析截面。主要分析截面极值正应力均以直线斜拉桥(弧长比例为0.00)极值正应力作为基准值,用差值和差值百分比表示弧长比例变化对主梁极值正应力的影响规律。成桥阶段不同弧长比例参考分析截面极值正应力差值见表2,极值正应力差值变化见图7。
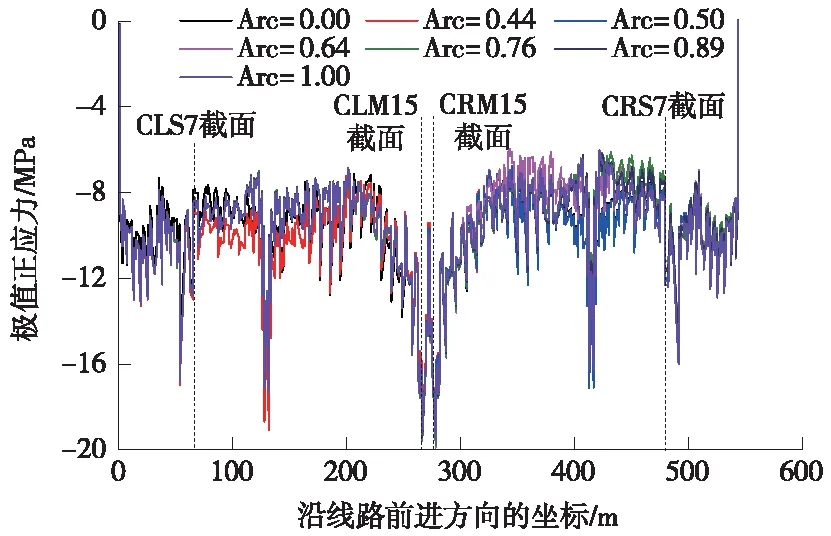
图6 成桥阶段主梁极值正应力对比

表2 参考分析截面极值正应力差值
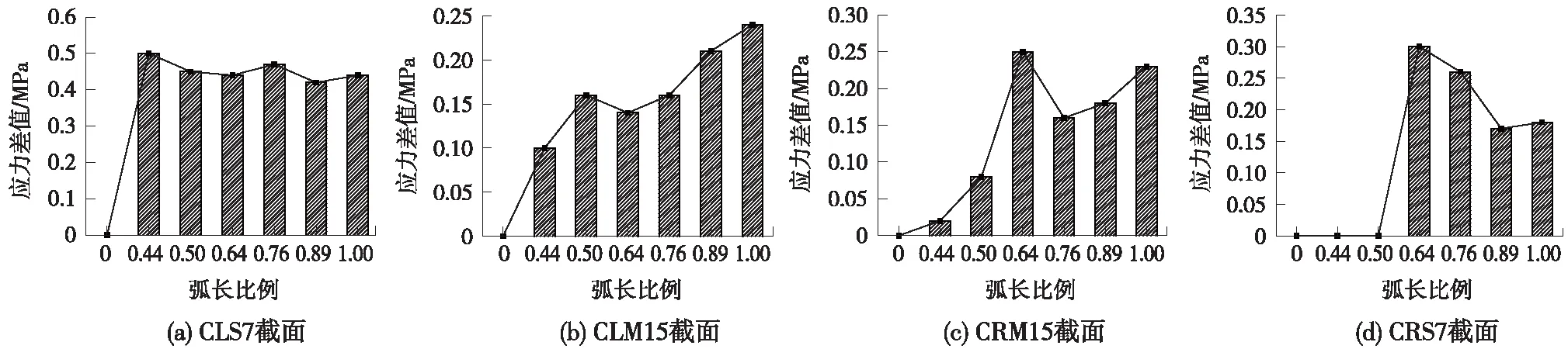
图7 参考分析截面极值正应力差值变化
由表2可知,弧长比例为0.44时,CLS7截面极值正应力相对直线斜拉桥对应截面变化最大,压应力增大0.50 MPa,增加4.05%,其相对变化量较小,表明主梁截面压应力极值受弧长比例影响较小。由图7可知,弧长比例为(0,1]时,主梁极值正应力均呈现一定程度的增加;弧长比例为(0,0.5]时,大部分截面极值正应力变化平缓,随着弧长比例增加,极值正应力逐渐增大,最大增加0.50 MPa;弧长比例为(0.5,0.76]时,CRM15截面和CRS7截面主梁极值正应力变化趋势较明显,有明显的突起,CLS7截面和CLM15截面主梁极值正应力也在逐渐增加,因此不建议以该范围弧长比例设计斜拉桥;弧长比例(0.76,1]为时,主梁正应力极值变化较为平缓,弧长比例对主梁正应力极值的影响逐渐减小。
2.2 主梁内力影响分析
(1)弧长比例对主梁弯矩的影响
曲线梁桥由于“弯-扭耦合”作用,主梁弯矩较直线桥大。而斜拉桥拉索可视为对主梁的弹性支承,其能减小主梁弯矩和扭矩,因此曲线斜拉桥主梁弯矩和扭矩随弧长比例的变化规律是主梁内力研究的重点。成桥阶段主梁弯矩对比图如图8所示。跨中至P5墩主梁主要参考分析截面相对于直线斜拉桥(弧长比例为0)的弯矩差值变化见图9。
由图8可知,当弧长比例变化为(0,1]时,跨中至P0墩主梁截面弯矩变化平缓,CLS12截面弯矩由33 939.5 kN·m增加到34 098.3 kN·m,增大0.5%,P1墩截面弯矩由12 707.0 kN·m增加到12 778.9 kN·m,增大0.6%,CLS4截面弯矩由5 968.3 kN·m增加到6 542.2 kN·m,增加574.0 kN·m,P2桥塔截面弯矩由8 382.1减小到8 138.7 kN·m,减小243.4 kN·m,跨中截面弯矩由11 163.0 kN·m增加到11 663.8 kN·m,增加了4.5%。由此可见,弧长比例变化对跨中至P0墩截面弯矩影响较小。
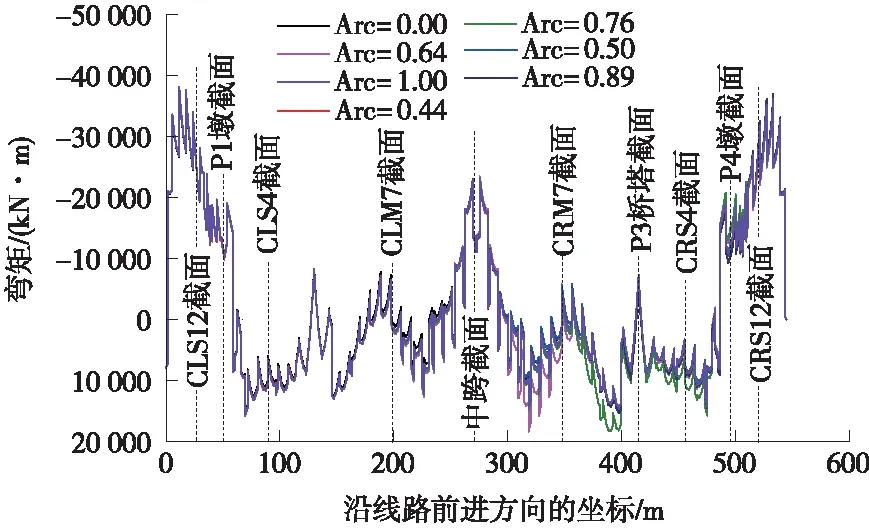
图8 成桥阶段主梁弯矩对比

图9 参考分析截面主梁弯矩差值变化图
由图9可知,当弧长比例为(0,0.5]时,跨中至P5墩主梁主要参考分析截面相对于直线斜拉桥(弧长比例为0)的弯矩差值不超过100 kN·m,变化率不超过1%,弧长比例为(0.89,1]时,主梁弯矩变化平缓,P3塔截面弯矩变化最大,增大1 316.4 kN·m;当弧长比例为(0.5,0.89]时,跨中至P4墩主梁截面弯矩变化明显,CRM7截面弯矩变化最大,增大3 430.7 kN·m。
综上所述,跨中至P0墩主梁截面纵向弯矩可按直线斜拉桥进行计算,当弧长比例在(0,0.5]时,全桥主梁纵向弯矩可按直线桥进行计算,当弧长比例为(0.5,0.89]∪(0.89,1]时,应按曲线斜拉桥对截面纵向弯矩进行计算,但跨中至P4墩主梁截面弯矩在弧长比例为(0.5,0.89]时变化明显,而在(0.89,1]时,变化平缓。
(2)弧长比例对主梁扭矩的影响
成桥阶段主梁扭矩对比图如图10所示,主要参考分析截面相对于直线斜拉桥(弧长比例为0)的扭矩差值变化如图11所示。

图10 成桥阶段主梁扭矩对比
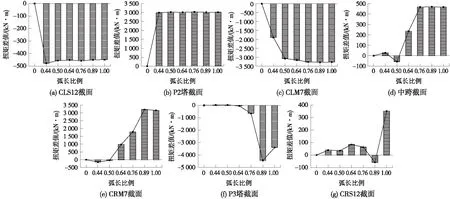
图11 参考分析截面主梁扭矩差值变化
由图10可知,当弧长比例为0时,主梁截面扭矩趋于0,当弧长比例大于0时,各截面扭矩增大,且各截面扭矩随弧长比例的增大而增大,表明随着弧长比例增大,曲线斜拉桥弯桥效应增强,主梁“弯-扭耦合”效应增强,扭矩不断增大。
由图11可知,当弧长比例为(0,0.5]时,跨中至P0墩主梁截面扭矩增长幅度较大,CLS12截面扭矩绝对值增长最少,增大455.04 kN·m,而CLM7截面扭矩绝对值增长最多,增大3 069.82 kN·m,与之相对,跨中至P5墩主梁截面扭矩增长幅度较小,CRM7截面扭矩绝对值增长最多,增大148.06 kN·m;当弧长比例为(0.5,1]时,跨中至P0墩主梁截面扭矩增长幅度较小,CLM7截面扭矩绝对值增长最多,增大211.34 kN·m,而跨中至P5墩主梁截面扭矩增大幅度较大,CRS12号截面扭矩绝对值增长最少,增大315.21 kN·m,P3桥塔截面扭矩绝对值增长最多,增大3 421.8 kN·m。
综上所述:当弧长比例为(0,0.5]时,弧长比例变化对跨中至P0墩截面扭矩影响较大,扭矩绝对值随弧长比例增大而增大,而对跨中至P5墩截面扭矩影响可忽略不计,该部分截面可按直线斜拉桥进行扭矩计算;当弧长比例(0.5,1]时,弧长比例变化对跨中至P0墩主梁截面扭矩影响可忽略不计,而对跨中至P5墩主梁截面扭矩影响较大,扭矩绝对值随弧长比例增大而增大。
2.3 支座反力影响分析
支座不仅是主梁承力、传力的重要部分,关系着整个结构的稳定、安全,同时其对改善主梁内力情况也有明显作用。曲线斜拉桥主梁在“弯-扭耦合”作用和索力的共同作用下,内外侧支座反力将受到不同程度的影响,支座受力情况变得复杂。随弧长比例变化,成桥阶段各支座反力变化见图12所示,全桥支座布置见图1。

图12 成桥阶段支座反力变化
由图12可知,当弧长比例大于0时,P0内侧支座反力由1 852.18 kN减小到1 395.14 kN,减小24.7%,减小明显且支座反力较小,此时P0处应采用大截面的横梁配重,以避免出现上拔力;当弧长比例大于0.89时,P5内侧支座反力由1 893.56 kN减小到1 511.42 kN,减小20.2%,减小明显且支座反力较小,此时P5处应采用大截面的横梁配重,以避免出现上拔力;当弧长比例为(0,0.5]时,P0、P1、P2内外侧支座反力变化明显且内外侧支座反力差值增大,P0内外侧支座反力差值变化最大,绝对值增大789.81 kN,而P3、P4、P5内外侧支座反力基本保持不变;当弧长比例(0.5,1]时,P0、P1、P2内外侧支座反力基本保持不变,而P3、P4、P5内外侧支座反力变化明显且内外侧支座反力总体呈现增大趋势。
综上所述,当弧长比例在(0,0.5]变化时,P0、P1、P2支座反力变化明显,需按曲线桥进行计算设计,而此时P3、P4、P5支座反力可按直线桥进行计算;当弧长比例在(0.5,1]变化时,P0、P1、P2支座反力基本保持不变,而此时P3、P4、P5支座反力变化明显。P0支座处应采用大截面的横梁配重,当弧长比例较大时,P5支座也应采用大截面的横梁配重,以避免出现上拔力。
2.4 主梁位移影响分析
基于梁+板单元模型特点,以内外侧梁肋竖向位移表征主梁竖向位移。成桥阶段主梁内外侧梁肋竖向位移对比图如图13、图14所示,主要参考分析截面内外侧梁肋竖向位移变化见图15。

图13 梁肋内侧竖向位移对比

图14 梁肋外侧竖向位移对比
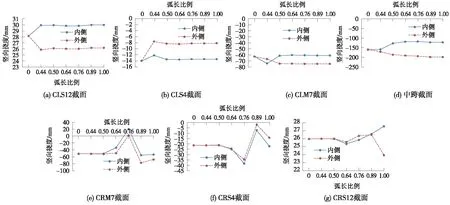
图15 成桥阶段梁肋竖向位移变化
由图13可知、图14可知,靠近中跨主梁竖向位移较大,而边跨主梁竖向位移相当对较小。随弧长比例变化,主梁内外侧梁肋竖向位移在中跨截面及P3桥塔截面附近有明显变化。
主梁内外侧梁肋竖向位移差值一定程度上反映了主梁扭矩的变化。由图15所示,随弧长比例增加,中跨主梁内外侧梁肋竖向位移差值持续增大。当弧长比例为(0,0.5]时,跨中至P0墩主梁内外侧梁肋竖向位移差值逐渐增大,中跨截面增幅最大,为59.05 mm,而跨中至P5墩主梁内外侧梁肋竖向位移差值基本保持不变;当弧长比例为(0.5,1]时,跨中至P0墩主梁内外侧梁肋竖向差值较大但趋于稳定,其中中跨主梁内外侧梁肋竖向位移差值最大,为76.02 mm。这与弧长比例对主梁扭矩的影响分析一致,进一步验证了弧长比例对主梁扭矩的影响规律。
综上所述,当弧长比例为(0.5,1]时,中跨主梁内外侧梁肋竖向位移差值较大,设计时应对主跨跨中主梁刚度进行加强,如对横隔板加密或增加横隔板厚度等。
3 结论与建议
通过建立不同弧长比例曲线斜拉桥有限元模型,对主梁应力、内力、位移以及支座反力等数据进行对比分析,可以得出以下结论:
(1)弧长比例在(0,0.5]时,大部分截面正应力极值变化平缓,随着弧长比例增加,正应力极值逐渐增大;弧长比例在(0.5,0.76]时,主梁正应力极值变化趋势较明显,不建议以该范围弧长比例设计斜拉桥;弧长比例在(0.76,1]时,主梁正应力极值变化较为平缓,弧长比例对主梁正应力极值的影响进一步减小。
(2)随弧长比例变化,跨中至P0墩主梁弯矩基本保持不变;弧长比例在[0,0.5]∪(0.89,1]时,全桥主梁弯矩基本保持不变,可按直线斜拉桥进行计算;弧长比例在(0.5,0.89]时,跨中至P4墩主梁截面弯矩变化明显,随弧长比例增加,弯矩绝对值增大。
(3)弧长比例在(0,0.5]时,弧长比例变化对跨中至P0墩主梁截面扭矩影响较大,扭矩绝对值随弧长比例增大而增大,而对跨中至P5墩主梁截面扭矩影响可忽略不计;弧长比例在(0.5,1]时,弧长比例变化对跨中至P0墩主梁截面扭矩影响可忽略不计,而对跨中至P5墩主梁截面扭矩影响较大,扭矩绝对值随弧长比例增大而增大。
(4)弧长比例在(0,0.5]变化时,P0、P1、P2支座反力变化明显且随弧长比例增加内外侧支座反力差值增大,而此时P3、P4、P5支座反力无变化;当弧长比例在(0.5,1]变化时,P0、P1、P2支座反力基本保持不变,而此时P3、P4、P5支座反力有明显变化。
(5)弧长比例在(0,1)时,弧长比例变化对两边跨内外侧梁肋竖向位移影响较小;弧长比例在[0.5,1]时,弧长比例变化对主跨跨中内外侧梁肋竖向位移影响较大且随着弧长比例增加,主跨跨中内外侧梁肋竖向位移差值增大。
曲线斜拉桥弧长比例选取建议:
(1)弧长比例在(0.5,0.89]时,跨中至P4墩主梁截面纵向弯矩较直线斜拉桥更大,对这部分截面应进行相应加强。
(2)弧长比例在(0,0.5]时,P0、P1、P2以及跨中附近主梁截面扭矩较直线斜拉桥更大,对这部分截面应进行相应加强;当弧长比例在(0.5,1]时,应对P0、P1、P2、跨中、P3、P4、P5附近主梁截面进行相应加强。
(3)弧长比例大于等于0.5时,应对主跨跨中位置梁段刚度进行加强,如加密横隔板布置或增加横隔板厚度等。
(4)P0支座处应采用大截面的横梁配重,当弧长比例较大时,P5支座也应采用大截面的横梁配重,以避免出现上拔力。
[1] 王伯惠.斜拉桥结构发展和中国经验·上册[M].北京:人民交通出版社,2003.
[2] 严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996.
[3] 林元培.斜拉桥[M].北京:人民交通出版社,2004.
[4] Leonhardt F, Zellner W. Cable-Stayed Bridges[J]. Iabse Survey Aipc Review Ivbh Berichte, 1980, 80(3):131-137.
[5] 李正仁,刘祖国.曲线斜拉桥的应用与展望[J].钢结构,2003,18(6):43-45.
[6] 朱琴忠,王立新,高波,等.曲线梁部分斜拉桥空间性能分析研究[J].城市道桥与防洪,2013(7):291-294.
[7] 万晓明.独塔单索面曲线斜拉桥力学性能研究[D].大连:大连理工大学,2009.
[8] 刘凯.曲线部分斜拉桥的几个设计参数研究[D].西安:长安大学,2013.
[9] 杨凯.PC箱梁曲线斜拉桥的静力性能研究[D].成都:西南交通大学,2015.
[10] 齐宏学.曲线部分斜拉—连续刚构桥力学行为研究[D].西安:长安大学,2009.
[11] 滕军,那琪,郭时安,等.高墩连续曲线梁桥以直代曲判别条件的确定[J].工程抗震与加固改造,2009,31(2):16-20.
[12] Wang P H, Yang C G. Parametric studies on cable-stayed bridges[J]. Computers & Structures, 1996, 60(2):243-260.
[13] Hegab H I A. Parametric Investigation of Cable-Stayed Bridges[J]. Journal of Structural Engineering, 1988, 114(8):1917-1928.
[14] 周友权.铁路新型钢-混组合独塔部分斜拉桥设计研究[J].铁道标准设计,2017,61(3):82-87.
[15] 尹晓明,朱益民,赵研峰.斜拉桥动力模型分析[J].铁道标准设计,2003(10):38-39.
[16] 赵勇,黄鼎业,李云贵,等.预应力混凝土板的等效荷载计算[J].建筑科学,2002,18(4):8-11.
