高速铁路无砟轨道路基填料动力试验荷载分析
2018-01-26王启云欧阳恒张丙强陈军浩赵卫华
王启云,欧阳恒,张丙强,陈军浩,赵卫华
(1.福建工程学院土木工程学院,福州 350108; 2.地下工程福建省高校重点实验室,福州 350108)
无砟轨道结构在高速铁路建设工程中得到越来越广泛的应用。在长期反复的高速列车荷载作用下,路基应保持土骨架的稳定而不产生轨道系统无法承受的附加变形[1],路基结构的长期稳定性是保证无砟轨道系统耐久性的前提条件。在对路基进行长期动力稳定性分析时,常常需要对路基填料进行动三轴试验或共振柱试验[2],或利用液压伺服加载系统[3]进行试验。在试验过程中,合理地模拟列车荷载对土体的作用是获得准确参数的基础。目前,由于室内动力试验研究侧重点不一,或出于试验条件的限制,其动力模拟和试验设计各不相同[4]。在进行室内试验时,一般分别要求给定相应的动应力幅值、频率以及加载波形等参数。表1是近年来文献中对铁路路基填料进行室内动力试验时采用参数。可以看出,对高速铁路路基填料开展室内试验时,采用的仪器多为动三轴试验系统,加载波形多为正弦函数,频率主要在1~5 Hz。实际上,加载波形和频率对土体累积变形、临界动应力比、动力参数的影响非常大[4]。路基中动应力随时间的变化是很复杂的,它与车速、轴重、深度、轨道不平顺等因素有关[5]。目前针对高速铁路无砟轨道路基土体开展室内试验时,施加的动荷载没有考虑列车速度、路基深度等因素的影响,试验结果未能正确地反映土体实际工程性状。国内外学者针对高速铁路无砟轨道路基承受的动荷载作用从现场测试[6]、数值计算[7]等方面进行了大量研究,但关于路基各结构层承受动荷载作用频率的还鲜有文献详细分析。因此,有必要针对高速铁路路基的动应力特性进行深入研究,从而给出简化的路基动荷载试验参数。

表1 铁路路基填料动力试验参数
本文基于ANSYS有限元平台,采用APDL语言建立CRTSⅡ型板式无砟轨道-路基系统三维有限元动力分析数值模型,模拟8辆编组的CRH380A型动车组的运行过程,计算分析路基结构的动应力及其频谱特性,结合文献中实测数据,探讨列车速度、轴重、轨道不平顺、路基深度等因素对动应力的影响。根据动应力时程曲线及其频响特征,采用全压周期的正弦函数建立路基不同深度处填料动力试验荷载表达式,为路基填料的动力试验提供输入参数,同时也可为无砟轨道路基结构设计分析提供荷载依据。
1 数值分析模型
1.1 数值模型及计算参数
参考无砟轨道单线路堤标准断面,建立CRTSⅡ型板式无砟轨道路基三维有限元模型。模型长度为26 m,计算深度为路基面以下9.7 m。由于主要的研究对象为路基结构,将钢轨简化为弹性点支承的连续梁,轨距为1.435 m,扣件间距取0.65 m。钢轨下扣件及胶垫等效为线性弹性元件,采用COMBIN14弹簧-阻尼单元,轨道与路基各结构层均采用SOLID45实体单元。轨道结构采用线弹性本构模型,计算参数见表2;路基结构层采用黏弹性本构模型,计算参数见表3。

表2 轨道系统计算参数

表3 路基计算参数
对有限元模型平行于线路方向的两个路基侧面和路基的底面施加三维一致黏弹性边界单元[13],同时约束垂直于线路方向的两个边界面沿线路走向的位移。建立的CRTSⅡ型板式无砟轨道-路基系统三维有限元模型如图1所示。

图1 CRTSⅡ型板式无砟轨道路基有限元模型
1.2 列车荷载模拟
本文研究的主要对象是路基,因此不考虑车辆与轨道的耦合,将高速列车荷载作为外部激励输入。由于涉及到机车的动力性能、线路平顺、路基刚度等[14]多种复杂的因素,作用于钢轨的列车动力荷载是一个非常棘手的问题。实际上,列车是由一系列长度大致相同的车厢组成,整体来看其轮载沿线路方向存在明显的周期性特征[14]。为此,假定列车为无限长度,将轮载视为4组单个集中荷载的组合,每组轮载均为周期性移动荷载,其周期为车辆的长度L,见图2。
考虑第①组轮载,假设列车运行速度为v,在t时刻该轮载位于Z1=vt处,则该轮载函数可表示为[14]
P1(t,Z)=P0δ(Z-vt)+F(t)δ(Z-vt)
(1)
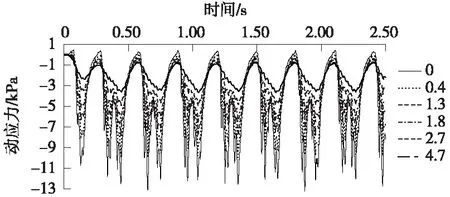
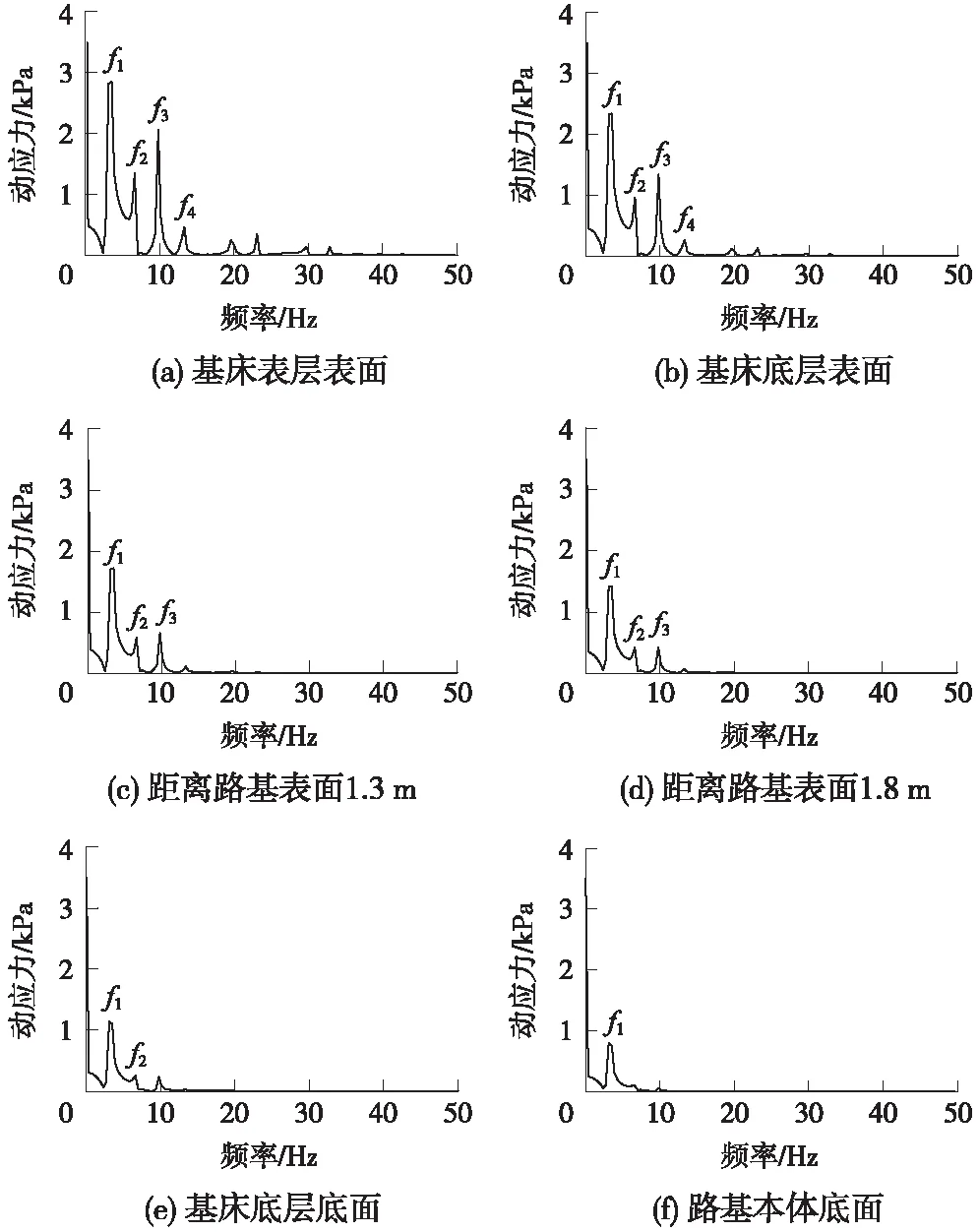
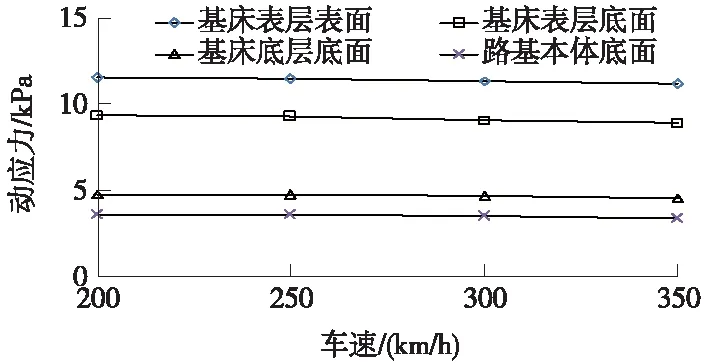
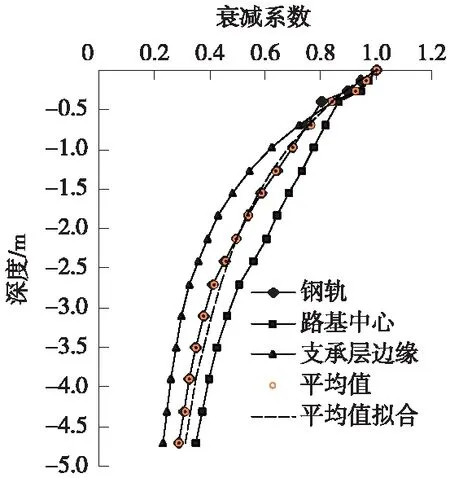
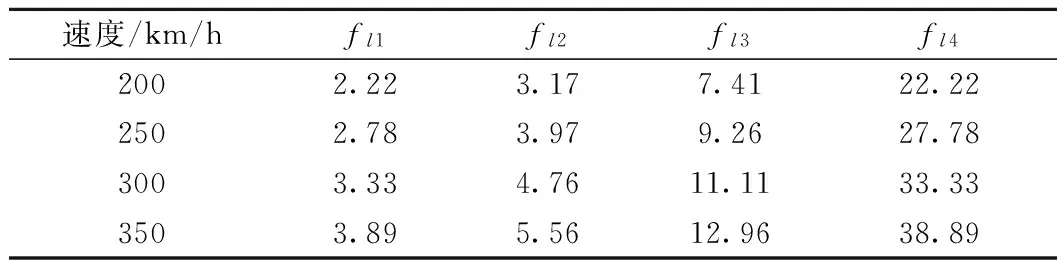
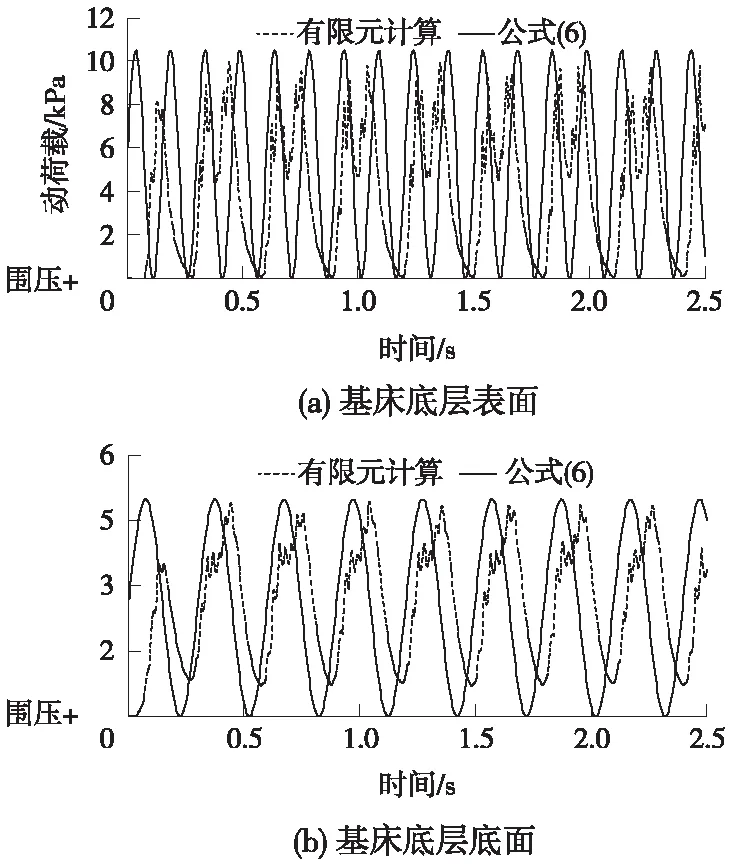
式中,vt-L/2 图2 列车荷载的分离与组合示意 附加荷载F(t)可用能反映不平顺、附加动荷和轨面波形磨耗效应的激励力来模拟,可表示为[14] F(t)=P1sinω1t+P2sinω2t+P3sinω3t (2) 分别针对不考虑和考虑轨道不平顺等因素两种工况,计算得到列车速度为300 km/h时钢轨处路基不同深度处的竖向动应力时程曲线如图3、图4所示。 图3 不考虑附加荷载路基竖向动应力时程 图4 考虑附加荷载路基竖向动应力时程 由图3可知,路基动应力时程具有显著周期性。路基表面以下0~0.4 m,动应力时程曲线包含16个峰值,与列车的16个转向架相对应,说明列车对基床表层土体的加卸荷过程由同一转向架的两对轮载共同完成;路基表面2.7 m以下,动应力时程曲线包含9个峰值,除时程曲线两端,每一个峰值对应荷载为相邻车厢的两个相邻转向架的轮载,说明列车对基床底层以下路基土体的加卸荷过程由相邻转向架的4对轮载共同完成。路基表面以下0.4~2.7 m深度范围内,动应力时程曲线包含16个峰值,但相邻车厢的转向架通过时,第1个转向架对应的峰值逐步衰减直至消失。从图4可以看出,在考虑轨道不平顺等因素时,基床表层的动应力时程曲线包含32个峰值,而基床底层底面与路基本体底面的动应力时程曲线峰值现象与图3基本一致,表明在每个车辆轮载经过时动应力存在峰值现象,路基承受荷载的作用明显比匀速恒载作用下更为剧烈。 对图3和图4动应力时程曲线进行快速傅里叶变换,获得相应的频谱曲线,如图5、图6所示。 从图5、图6可以看出,路基承受荷载的作用频率沿路基深度逐渐衰减,基床表层承受的荷载作用频率存在4个明显峰值f1、f2、f3、f4,其中f1、f2、f3对应峰值特征尤为显著,基床底层和路基本体承受的荷载作用频率分别存在3个峰值、1~2个峰值,其中f1对应峰值特征尤为显著。比对图5、图6可知,在不考虑和考虑轨道不平顺等因素两种工况条件下,路基各结构层承受荷载的4个峰值频率一致,说明轨道不平顺没有改变路基承受荷载作用的主频。 在考虑轨道不平顺等因素的列车荷载作用下,路基各结构层的动应力幅值σd1与匀速恒载作用下路基各结构层的动应力幅值σd2见表4,定义路基动应力轨道不平顺影响系数φs=σd1/σd2。取时速为5 km的列车速度为准静态标定速度。动力系数φd为路基动应力幅值与准静态条件下路基动应力幅值之比,即φ=σd1/σ0。 图5 不考虑附加荷载路基动应力典型频谱曲线 图6 考虑附加荷载路基动应力典型频谱曲线 位置σd1/kPaσd2/kPaσ0/kPaϕsϕd基床表层表面13.4511.3511.161.191.21基床底层表面9.969.219.081.081.10基床底层底面4.964.674.661.061.06路基本体底面3.653.473.461.051.05 可以看出,在本文计算条件下,由轨道不平顺因素引起轮轨力增大,导致路基动应力为匀速恒载作用下的1.19~1.05倍,且从路基面往下轨道不平顺影响系数逐渐减小,随着深度增加,动应力与准静态应力逐步接近,说明轨道不平顺等因素对路基动应力的影响主要集中在基床表层与底层。从表4还可以看出,动应力轨道不平顺影响系数与动力系数基本相同,说明轨道不平顺是引起路基动应力增大的主要原因。胡一峰等[5]基于实测结果,建议无砟轨道路基动应力动力系数取1.0~1.3,詹永祥等[15]给出了遂渝线无砟轨道板桩结构路基结构的实测动力系数在1.05~1.2,刘钢等[16]列出了武广高铁实测路基面平均动应力对应的综合动力影响系数在0.98~1.37,平均值为1.2。本文计算得到的路基动应力轨道不平顺影响系数和动力系数与前述文献的数值较为接近,表明本文数值模型与计算结果是合理的。综合本文计算结果和相关文献实测数据,建议路基动应力轨道不平顺影响系数φs取1.0~1.3,路基表面的φs取1.1~1.3。 在匀速恒载作用下,路基表面动应力幅值与列车速度的关系曲线如图7所示。 图7 动应力与车速的关系 由图7可知,列车在时速200~350 km运行时,路基动应力随着速度的增加而略有减小,且变化幅度小于10%,这种规律与遂渝线无砟轨道板桩结构路基动应力[15]变化规律一致,这是由于列车速度超过临界速度。总体而言,列车速度对路基动应力幅值影响不大。 在不考虑轨道不平顺等因素的列车荷载作用下,不同速度时路基表面动应力幅值与列车轴重的关系曲线如图8所示。 图8 动应力与轴重的关系 可以看出,随着列车轴重增加,路基动应力几乎成线性增大。对路基面动应力与轴重的关系曲线回归分析,结果表明,列车轴重每增加10 kN,无砟轨道路基面动应力增加0.81 kPa。如考虑轨道不平顺影响系数,列车轴重每增加10 kN,无砟轨道路基面动应力增加0.97 kPa,数值与据京津、武广、京沪先导段实测数据[17]统计数值0.87~1.18 kPa接近。 动应力衰减系数与深度关系曲线如图9所示。可以看出,基床表层范围内,不同位置的动应力衰减率基本一致,基床表层以下由路基中心向外,动应力衰减率逐渐增大。动应力在基床表层底面处平均衰减系数为0.838,在基床底层底面处平均衰减系数为0.413。武广、京津、京沪高铁无砟轨道路基现场测试[16-18]表明:基床表层底面动应力衰减系数在0.66~0.92,基床底层底面处动应力衰减系数在0.23~0.40。本文计算得到的动应力衰减系数与现场实测结果偏差在10%以内,可认为本文数值模拟得到的动应力衰减系数与深度关系曲线是合理的。路基动应力平均衰减系数φ(z)与深度z的关系可表示为 (3) 图9 动应力衰减系数与深度关系 为获得路基承受列车荷载的作用频率,对路基动应力时程曲线进行快速傅里叶变化,得到路基承受荷载的作用频率,如表5所示。 从表5可以看出,列车速度越大,路基承受荷载的作用频率越大,且幅值频率基本满足f2=2f1、f3=3f1、f4=4f1的关系。 表5 路基承受荷载的作用频率 Hz 就路基的长期动力稳定性而言,一般情况低频部分起控制作用,因此在对路基填料进行动力试验时,应将低频率作为控制频率[12]。列车轮载通过无砟轨道传递至路基,使路基结构受到荷载的作用,列车荷载的作用频率f可表示为[12] f=v/l (4) 式中,v为列车速度;l为扰动波长。 CRH380A型动车组轴距存在l1=L=25 m、l2=17.5 m、l3=7.5 m、l4=2.5 m四组,由式(4)计算得到对应荷载频率fl1、fl2、fl3、fl4,如表6所示。 表6 列车荷载作用频率 Hz 对比表5和表6,可以发现扰动波长为车辆长度L对应的频率fl1与f1基本一致,路基承受荷载的4个主要频率可表述为f1=fL、f2=2fL、f3=3fL、f4=4fL。列车荷载最大作用频率远大于路基承受荷载的作用频率,说明无砟轨道具有良好的扩散作用,使转向架车轴对应的频率特性不明显,且大幅度降低了路基承受荷载的作用频率。 高速列车作用下,路基承受荷载的幅值和频率是室内试验主要的模拟对象。通过前述分析,路基各结构层的动应力幅值σmax可采用以下函数来描述 σmax=0.81P0φsφ(z) (5) 式中,P0为列车轴重,kN;φs为路基表面动应力轨道不平顺影响系数,φs建议取1.1~1.3;φ(z)为动应力沿深度衰减系数。 现有研究表明,采用拉压等幅循环应力模拟高速铁路荷载作用将引起很大误差[4],且从动应力时程曲线可以看出,在列车荷载经过时路基土体始终处于受压状态,因此针对能输出正弦函数荷载的试验设备,对不同深度的填料进行试验时,施加的动荷载可采用全压周期的正弦函数表示 (6) 式中,w为加载频率;t为加载时间。 依据路基各结构层所受荷载加载过程及其频谱特征,在对基床表层填料开展动力试验时,最大加载频率取车厢长度对应频率v/L的3倍,即w=3v/L;对基床底层填料开展动力试验时,最大加载频率取车厢长度对应频率v/L的2倍,即w=2v/L;对路基本体填料开展动力试验时,最大加载频率取车厢长度对应频率v/L,即w=v/L。 以列车轴重P=14 kN、运行速度v=300 km/h为例,利用式(6)计算得到基床底层表面与底面处填料进行动力试验时动荷载输入时程,如图10所示。 图10 路基填料动力试验曲线 从图10可以看出,采用式(6)得到的填料动力试验荷载与有限元计算得到动应力幅值、曲线形态均能较好地吻合,表明本文给出的动力试验参数是合理的。 (1)基床表层土体的加卸荷过程由同一转向架的两对轮载共同完成,随着深度的增加,路基土体的加卸荷过程由同一转向架的2对轮载共同完成逐步转至由相邻转向架的4对轮载共同完成。 (2)当列车速度在200~350 km/h范围内增加时,路基动应力变化不明显,但路基承受荷载的作用频率呈线性增大。列车轴重每增加10 kN,路面的动应力增加0.97 kPa。路基动应力随深度增加而迅速衰减,并与准静态下应力逐步接近。 (3)轨道不平顺等因素引起路基动应力幅值明显增加,其影响系数可取1.0~1.3,但轨道不平顺没有改变路基承受荷载的主频。无砟轨道路基承受的荷载存在4个峰值频率,分别为列车车厢长度对应频率v/L的1~4的整数倍。 (4)依据路基承受动应力的时程曲线及其频率特征,采用全压正弦函数建立路基填料动力试验荷载表达式。对基床表层、基床底层、路基本体的填料进行动力试验时,加载频率分别取车厢长度对应频率v/L的3、2、1倍。 需要说明的是,本文给出的路基填料动力试验函数未考虑轨道结构型式、路基结构型式及其刚度等因素的影响,因此需要积累更多的实测数据,通过计算、统计分析,得到更为准确的动力加载参数。 [1] 刘晓红.高速铁路无砟轨道红黏土路基动力稳定性的研究[D].长沙:中南大学,2011. [2] 刘晓红,杨果林,方薇.武广高铁无砟轨道路堑基床长期动力稳定性评价[J].中南大学学报(自然科学版),2011,42(5):1393-1398. [3] 冷伍明,刘文劼,周文权.振动荷载作用下重载铁路路基粗颗粒土填料临界动应力试验研究[J].振动与冲击,2015,34(16):25-30. [4] 黄博,丁浩,陈云敏.高速列车荷载作用的动三轴试验模拟[J].岩土工程学报,2011,33(2):195-202. [5] 胡一峰,李怒放.高速铁路无砟轨道路基设计原理[M].北京:中国铁道出版社,2010. [6] 孔祥辉,张思峰,蒋关鲁,董志泓.土质路基板式无砟轨道基床动力特性研究[J].铁道标准设计,2014,58(6):10-14. [7] 王启云,张家生,孟飞.不均匀沉降对无砟轨道路基动力特性的影响[J].铁道标准设计,2014,58(10):17-21. [8] 杨广庆,管振祥.高速铁路路基改良填料的试验研究[J].岩土工程学报,2001,23(6):682-685. [9] 胡安华,蒋关鲁,魏永幸,王智猛.200 km/h客货共线铁路红层泥岩基床填料动力特性研究[J].铁道学报,2010,32(6):120-123. [10] 宫全美,罗喆,袁建议.提速铁路基床长期累积沉降及等效循环荷载试验研究[J].铁道学报,2009,31(2):88-93. [11] 邓国栋,张家生,王启云,等.高速铁路粗粒土填料动力参数试验研究[J].铁道科学与工程学报,2014,11(2):76-83. [12] 郭建湖.高速铁路碎石类A、B组填料的动力特性研究[J].土工基础,2012,26(5):116-120. [13] 刘晶波,谷音,杜义欣.一致黏弹性人工边界及黏弹性边界单元[J].岩土工程学报,2006,28(9):1070-1075. [14] 梁波,罗红,孙常新.高速铁路振动荷载模拟研究[J].铁道学报,2006,28(4):89-94. [15] 詹永祥,蒋关鲁,胡安华,等.遂渝线无砟轨道桩板结构路基动力响应现场试验研究[J].岩土力学,2009,30(3):832-835. [16] 刘钢,罗强,张良,等.列车荷载作用下无砟轨道路基动应力特性分析[J].铁道学报,2013,35(9):86-93. [17] 叶阳升.高速铁路路基动力响应特性[J].铁道建筑,2015(10):7-12. [18] 郭志广,魏丽敏,何群,等.武广高速铁路无砟轨道路基动力响应试验研究[J].振动与冲击,2013,32(14):148-152.
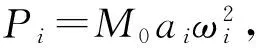
2 路基动应力影响因素分析
2.1 轨道不平顺



2.2 列车速度
2.3 列车轴重

2.4 路基深度
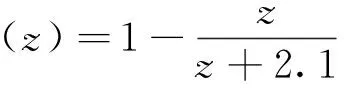
3 路基承受的荷载作用频率

4 路基填料动力试验参数
5 结论
