R1234yf/R134a二元混合工质的热物理性质
2018-01-25孙维栋
孙维栋,张 鹏,张 昌
(武汉纺织大学,湖北武汉 430200)
1 前言
虽然目前R134a能够很好地替代之前的R12并被广泛用于汽车空调,但欧洲在2006年通过的F-Gas法案规定,2017年出厂的新车不得使用GWP大于150的制冷剂[1]。GWP值近1430的R134a将会被逐步淘汰。R1234yf在毒性、燃烧性及安全性方面的表现与 R134a 相当[2,3],其 GWP只有4。R1234yf与R134a的热力性质相当[4],有可能在不改变设备的前提下替代R134a。但是,R1234yf与润滑油的互溶性和与系统中所有材料的相容性研究较为滞后。为了在原有系统稳定工作的前提下降低制冷剂的GWP值,改用R1234yf/R134a混合制冷剂是一种可行的方法。国内外学者对R1234yf/R134a混合物做了大量的研究工作。Akasaka R等测量了R1234yf/R134a的临界参数,并用Helmholtz能量方程建立了热力学模型[5]。Kamiak T等对R1234yf/R134a的气液相平衡特性进行了实验研究[6~8]。Chen Q等测量了R1234yf/R134a在气相区的PVTx性质[9]。Bi SS等测量了R1234yf/R134a的表面张力和液体运动黏度[10]。Kedzierski M等对共沸物R513A(R1234yf/R134a 56/44wt%)在微肋管中的流动沸腾换热性能进行了研究[11]。Schultz K 及 Kasai K 等分别对R513A和D4Y(R1234yf/R134a 60/40wt%)在螺杆式冷水机组中的循环性能进行了研究[12,13]。Lee Y等研究了不同工况,不同组分配比时R1234yf/R134a在热泵实验台中的运行性能,且其指出当R134a的质量分数高于10%时混合物的可燃性会消失[14]。但是,目前关于R1234yf/R134a混合物焓、熵等热力性质方面的文献报导较少。本文用PR方程结合vdW和HV混合法则建立R1234yf/R134a二元混合工质的热物性模型,分析发现2种方式均可以较好地描述R1234yf/R134a的VLE特性,对混合物气相区的PVTx性质也具有较高的计算精度。之后根据余函数法推导出混合物的焓、熵等热力性质,为R1234yf/R134a直接替代的工程研究提供计算模型。
2 状态方程和混合法则
2.1 状态方程
对于R1234yf/R134a混合物,本文采用的PR状态方程表达式为[15]:
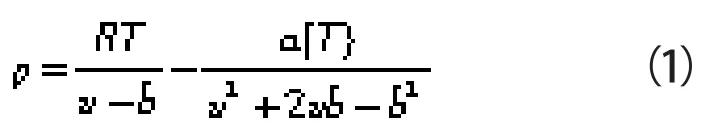
其中
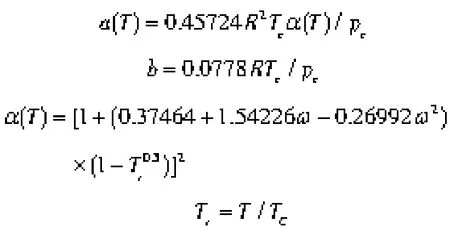
式中 p——压力
R—— 通用气体常数,J /(mol·K),R=8.314 J/(mol·K)
v——摩尔体积
T——温度
a——引力项
b——协体积项
pc——临界压力
Tc——临界温度
ω——偏心因子
方程所需2种工质的临界参数及偏心因子见表1。

表1 R1234yf和R134a的部分物性参数[16]
2.2 混合法则
状态方程用于混合物计算时需结合相应的混
合法则,vdW(van der Waals)混合法则是被广泛

式中 am——混合物的引力项
bm——混合物的协体积相
aii——i组分的引力项
bii——i组分的协体积相kij——二元交互系数
HV混合法则形式如下[17]:

式中 C——常数,对于PR方程,C=0.623225
本文中τii=0,αii=0,αij=0.3;Aij和 Aji是拟合参数。
3 混合物热物理性质计算结果及分析
3.1 VLE关联结果的精确度
本文通过使63个VLE试验点数据上的目标函数值最小[6],得到vdW混合法则的交互系数kij和HV混合法则的拟合参数Aij,Aji。目标函数为:

式中 N——VLE试验点的总数
pexp,i——泡点压力试验值
pcal,i——泡点压力计算值
yexp,i——R1234yf气相摩尔分数试验值
ycal,i——R1234yf气相摩尔分数计算值
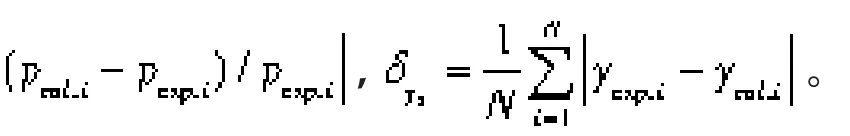

表2 PR+vdW和PR+HV对混合物VLE数据的关联结果
表2还列出PR方程结合vdW、HV混合法则分别对各组试验数据及总试验数据进行关联得出的结果。对总试验数据进行关联时,δp分别为0.361%、0.50%,δy2分别为2.350×10-3、2.457×10-3,2种方式的计算精度均较高。图1是不同温度下混合物泡、露点压力与摩尔组分的关系曲线,其中,vdW混合法则的kij为0.019,HV混合法则的Aij,Aji随温度变化取相应值。

图1 不同温度下泡、露点压力随摩尔组分的变化
3.2 气液相平衡特性分析
本文采用由PR方程结合vdW混合法则建立的热物性模型计算R1234yf/R134a的热物理性质。图1显示该混合物泡、露点压力差较小,为近共沸混合物且同温度下泡点压力存在最大值。泡、露点压力的变化幅度较小,这主要是因为同温度下R1234yf的饱和压力与R134a相近。为清晰表达气液相平衡状态,将图1中对应温度、液相摩尔组分下R1234yf气相组分与液相中组分的绝对差值描述为图2。由图2可知,该混合物存在共沸点。随着温度的升高,共沸点逐渐向左平移,R1234yf在两相中的组分差值逐渐减小,曲线逐渐变得平缓。这是因为随着温度的升高,或压力增加,混合物的物性会发生变化。温度升高时液体分子间的作用力变小、表面张力、液相黏度及密度变小,而气体分子间的作用力变大、气相黏度及密度变大,使得两相组分差别减小。

图2 不同温度下气、液相组分差值随液相摩尔组分的变化
不同压力下泡、露点温度随摩尔组分的变化如图3所示。

图3 不同压力下泡、露点温度随摩尔组分的变化
由图3可知,同压力下混合物的泡、露点温度差较小,且存在比纯工质组成的饱和温度都低的泡、露点温度。泡、露点温度差较小也是因为同压力下R1234yf的饱和温度与R134a相近。为清晰表达混合物的温度滑移特性,将图3中对应压力、摩尔组分下混合物泡、露点温度差的情况描述为图4。由图4可知,随着压力的增加,温度滑移与摩尔组分的关系曲线逐渐变得平缓,温度滑移均值逐渐变小,共沸点逐渐向左平移。当混合物的压力大于400 kPa,R1234yf的摩尔分数为0.45~0.60时,温度滑移均小于0.05 K。当R1234yf的摩尔分数为0.533(与R513A的组成几乎一致)时,温度滑移最大约为0.01 K。在压力为200kPa,R1234yf的摩尔分数为0.178时,温度滑移最大仅为0.28 K。

图4 不同压力下温度滑移随摩尔组分的变化
3.3 气相区PVTx性质计算结果的精确性
为了比较模型在气相区的精确性,将计算结果与文献[9]中的试验数据进行了比较,如图5,6所示。气相区压力、密度的相对偏差分别在1.74%、2.60%以内,平均绝对偏差分别为0.834%、1.050%,模型对于气相区PVTx性质同样具有较高的计算精度。

图5 气相区压力的相对偏差

图6 气相区密度的相对偏差
4 R1234yf/R134a的热力性质
4.1 混合物焓、熵的计算
对于混合物的焓和熵,本文采用余函数法[19]计算。余自由能和余自由熵可由PR方程根据热力学关系式推导得出,其表达式分别如下:

式中 v0—— 与实际气体同温同压下理想气体的比容,v0=RT/p
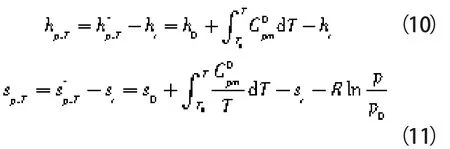
式中 h0——计算基准参考点的焓值
s0——计算基准参考点的熵值
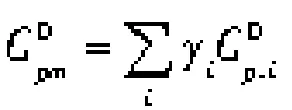

4.2 热力性质计算结果对比
通过已建立的热物性模型结合式(7)~(13)即可计算出混合物的热力性质。研究表明,R134a的质量分数为10%~11%即摩尔分数为0.11~0.12时,混合物的可燃性会消失且GWP小于150[14]。因此,本文把摩尔组分比为0.89/0.11、温度为253.15~328.15 K时R1234yf/R134a的相平衡状态及部分热力性能数据列于表3,作为计算结果的举例展现。

表3 R1234yf/R134a(0.89/0.11)相平衡时液相、气相的部分热力性质
为比较热力性质计算结果,以1MPa时露点(温度为 318.15 K)作基准点,焓为 0 kJ/kg,熵为 0 kJ/(kg·K),将R1234yf的摩尔分数为0.457时混合物过热性质的计算值与用文献[9]中维里方程计算出的结果进行了比较,得出气体焓、熵的最大差值分别为3.287 kJ/kg、0.0096 kJ/(kg·K),如图7所示。将R1234yf的摩尔分数为0.532时,253.15~333.15K范围内混合物的相平衡状态计算值与文献[22]中的数据进行了比较,得出相平衡状态液体和气体焓、熵值的相对偏差分别为-0.92%~0.08%、-0.17%~0.08%、-0.61%~0.06%、-0.18%~0.06%,如图8所示。计算结果表明,偏差在1.0%以下,可供工程计算使用[23~27]。
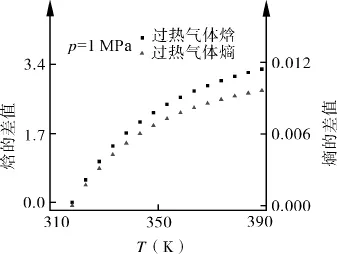
图7 过热状态焓、熵值与用文献[9]中方程计算得出结果的比较

图8 相平衡状态焓、熵值与文献[22]中数据的比较
5 结论
(1)用PR方程结合vdW和HV 2种混合法则均可很好地描述R1234yf/R134a的VLE特性,本文中PR方程结合vdW混合法则的整体计算精度略高,压力的平均绝对偏差为0.361%。
(2)R1234yf/R134a具有明显的近共沸特性,存在共沸点,且R1234yf的摩尔分数为0.533时,混合物在压力为400~1700kPa的温度滑移最大约0.01K;当压力为200 kPa,摩尔组分比为0.178/0.822时,温度滑移达到最大为0.28 K。
(3)模型对于混合物热力性质计算结果的精确度满足工程分析的需求,可用于替代分析和系统性能计算。
[1] 陈江平,施骏业,赵宇.国内外汽车空调系统发展动向[J].化工学报,2008,59(S2):9-13.
[2] 朱明善,史琳.制冷工质燃烧(分解)及生成有毒气体的探讨[J].制冷学报,2011,32(3):1-5.
[3] 曹霞.HFO-1234yf——新一代汽车空调制冷剂[J].制冷与空调,2008,8(6):55-61.
[4] 孙维栋,张鹏,张昌.R1234yf汽车空调制冷剂的理论循环性能分析[J].制冷与空调,2016,16(10):33-37.
[5] Akasaka R,Higashi Y,Yamada Y,et al.Thermodynamic properties of 1,1,1,2-tetrafluoroethane (R-134a) + 2,3,3,3-tetrafluoropropene (R-1234yf) mixtures:Measurements of the critical parameters and a mixture model based on the multi-fluid approximation[J].International Journal of Refrigeration,2015,58:146-153.
[6] Kamiaka T,Dang C,Hihara E.Vapor-liquid equili-brium measurements for binary mixtures of R1234yf with R32,R125,and R134a[J].International Journal of Refrigeration,2013,56(3):965-971.
[7] 陈日帅,祁影霞,吴东.混合制冷剂R1234yf/R134aPVTx性质的实验研究[J].制冷学报,2016,37(1):18-25.
[8] 张佳妮,祁影霞.近共沸制冷剂R134a/R1234yf的PVTx性质的实验研究[J].制冷技术,2016,36(2):34-39.
[9] Chen Q,Qi H M,Zhang S Q,et al.An experimental study of PVTx properties in the gas phase for binary mixtures of HFO-1234yf and HFC-134a[J].Fluid Phase Equilibria,2015,385:25-28.
[10] Bi S S,Cui J W,Zhao G J,et al.Surface tension and liquid viscosity measurement for binary mixtures of R134a with R1234yf and R1234ze(E)[J].Fluid Phase Equilibria,2016,414:60-64.
[11] Kedzierski M A,Park K J.Horizontal convective boiling of R134a,R1234yf/R134a,and R1234ze(E) within a micro-fin tube[J].Journal of Enhanced Heat Transfer,2013,20(4):333-346.
[12] Schultz K,Kujak S.System drop-in tests of R134a alternative refrigerants(ARM-42a,N-13a,N-13b,R-1234ze(E),and OpteonTMXP10) in a 230-RT water-cooled water chiller[R].AHRI Low-GWP AREP Report NO.7,2013.
[13] Kasai K,Johnson P.System drop-in test of R134a alternative fluids R-1234ze(E) and D4Y in a 200 RT air-cooled screw chiller[R].AHRI Low-GWP AREP Report NO.25,2013.
[14] Lee Y,Kang D G,Jung D.Performance of virtually non-flammable azeotropic HFO1234yf/HFC134a mixture for HFC134a applications[J].International Journal of Refrigeration,2013,36(4):1203-1207.
[15] Peng D Y,Robinson D B.A new two-constant equation of state[J].Industrial & Engineering Chemistry Fundamentals,1976,15(1):59-64.
[16] Lemmon E W,Huber M L,Mclinden M O.NIST standard reference database 23:reference fluid thermodynamic and transport properties-REFPROP9.0[R].2010.
[17] Huron M J,Vidal J.New mixing rules in simple equations of state for representing vapourliquid equilibria of strongly non-ideal mixtures[J].Fluid Phase Equilibria,1979,3(4):255-271.
[18] Renon H,Prausnitz J M.Local compositions in thermodynamic excess functions for liquid mixtures[J].AIChE Journal,1968,14(1):135-144.
[19] 童钧耕,吴孟余,王平阳.高等工程热力学[M].北京:科学出版社,2006:99-105.
[20] Brown J S,Zilio C,Cavallini A.Critical review of the latest thermodynamic and transport property data and models,and equations of state for R-1234yf[C]//2010 International Refrigeration and Air Conditioning Conference.Purdue University,2010.
[21] Mclinden M O,Gallagher J S,Weber L A,et al.Measurement and formulation of the thermodynamic properties of refrigerants 134a and 123[J].ASHRAE Transactions,1989,95.II.
[22] AP1700物质物性计算查询平台[EB/OL].http://www.ap1700.com/.
[23] 周响,王学生,张崇.压缩机冷却器内气液不互溶两相流热力计算[J].流体机械,2015,43(2):37-40.
[24] 李斌,於秋霞,熊姝涛,等.CNG-2型气瓶用玻璃纤维增强材料耐腐蚀性能分析[J].压力容器,2015,43(1):1-7.
[25] 张姗姗,颜文旭,公群.高压脉冲电场处理室多物理场仿真研究[J].包装与食品机械,2016,34(3):38-41.
[26] 金世杰,费良军,傅渝亮.土壤水分再分布特性研究进展[J].排灌机械工程学报,2016,34(3):73-
