基于简化描述符的仿射不变图像匹配算法

李记鹏，尹颜朋

（四川大学计算机学院，成都 610065）

0 引言

图像匹配是计算机视觉的一个重要分支，广泛应用于三维重建、目标识别、图像检索等领域。基于特征的匹配方法由于计算量少、速度快得到了研究者的青睐，近年来大量的局部特征检测子涌现出来，这些检测子都具有平移不变性，Harris检测子[11]对于旋转也具有不变性，Harris-Laplace,Hessian-Laplace以及高斯差分区域检测子具有尺度不变性[12-15]，其他一些区域检测子如 Harris-affine,Hessian-affine,MSER（Maximally Sta⁃ble Extremal Region）对于图像的仿射变换具有一定的适应性[16,13,5]。Lowe提出的特征检测方法将SIFT（Scale Invariant Feature Transform）检测子与SIFT描述符相结合，具有尺度、平移、旋转不变性，对光照、几何变换有一定的适应性。相关文献表明相对于其他描述符而言，SIFT描述符性能更加稳定[17]，因此被广泛应用于图像匹配，然而SIFT特征描述符维度过高，匹配图像的时间开销很大而且不具备仿射不变性。YanKe等提出PCA（Principal Components Analysis）-SIFT[2]方法有效的降低了描述符的维度，提高了图像匹配的速度，但是该方法的降维操作时间复杂度过高。ZhipingZhou等提出的 MDS（Multidimensional Scaling）-SIFT[3]方法在一定程度上克服了该问题，同时引入局部纹理特征约束提高了匹配的精度。XinminZhou[4]提出一种方法使用圆形区域替代正方形区域，然后计算每个子区域梯度方向分布，该方法极大的简化了描述符生成的过程，提高了匹配速度。上述方法虽然提高了图像匹配的效率，但是都不具备仿射不变性。J.Matas[5]等提出一种适用于宽基线图像匹配的方法，提取图像的MSER特征进行图像匹配，WenchaoHu等将MSER特征与SIFT特征相结合提出一种对于仿射形变具有较好鲁棒性的匹配算法[6]，但是这些方法依然不具有完全仿射不变的特性。J.M.Morel等将摄像机的成像过程近似为仿射变换，通过模拟摄像机位置变化产生的仿射形变提出一种完全仿射不变的图像匹配算法即ASIFT（Affine-SIFT）[7]，然而该算法时间开销太大。

本文将简化描述符与ASIFT的模拟方法相结合提出一种完全仿射不变的匹配算法，实验证明该方法对于仿射形变较大的图像具有较好的鲁棒性，匹配速度明显优于ASIFT。

1 基于简化描述符的仿射不变匹配算法

1.1 基于圆形邻域的简化描述符

SIFT生成描述符时，为了保证旋转不变性在统计梯度方向之前需要将整个采样区域旋转至主方向，由于SIFT采样区域为方形区域旋转前后无法完全重叠，尤其是角落区域的像素点旋转后大部分均不在重叠区域如图1（a）所示，因此采用相同尺寸的方形区域生成描述符肯定会产生很大的误差。在实践中相关算法为了克服该误差往往采用更大的方形区域生成描述符，这种做法不可避免的带来了了冗余的像素旋转操作，增加了运行时间。圆形区域则不相同，对于旋转操作具有更好的不变性，旋转前后覆盖的像素完全一致如图 1（b）所示。

图1 方形区域和圆形区域比较

因此本文提出一种在圆形邻域内使用扇形区域生成描述符的方法，具体过程如下：

（1）使用SIFT方法在尺度空间中寻找图像的关键点，同时确定主方向。

（2）在相应的尺度空间中以关键点为中心产生一个圆形区域，计算像素梯度，将圆形区域旋转至主方向，对梯度做高斯加权。

（3）将圆形区域分为2×2个扇形子区域，在每个扇形区域内统计8个方向的梯度直方图如图2（b）所示。

（4）将4个扇形的梯度直方图合并得到32维的描述符然后进行归一化处理，以降低光照变化对描述符的影响。

SIFT生成描述符时以关键点为中心生成一个方形邻域，然后将其分为16个子区域，在每个在区域内统计8个方向的梯度直方图如图2（a）所示，最终生成128维描述符。尽管本文方法也需要统计梯度直方图，但是只需要在4个扇形区域上统计，统计次数比SIFT少了12次，另外本文算法的描述符维度降低了64维，在进行描述符相似度的计算时，使用该描述符可以大大降低计算量，提高匹配效率。

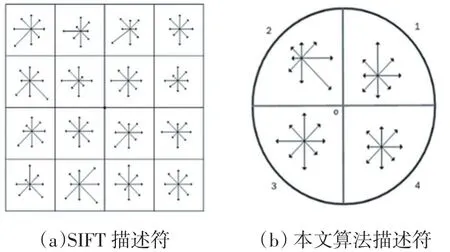
图2 描述符对比

1.2 仿射不变匹配算法

降维后的描述符与SIFT描述符一样具有尺度，旋转不变性并且对于光照、强度变化有一定的适应性，而且匹配速度有一定提高，然而仍然不具有仿射不变性。本文受ASIFT模拟思想的启发，通过模拟摄像机位置变化产生的形变克服这一缺陷，提出一种完全仿射不变的匹配算法。

在仿射相机模型中，摄像机成像过程被简化为一个仿射变换，该仿射变换存在唯一的SVD分解：

其中λ>0 λ>0,λt是A的行列式，Ri表示旋转，与相应的对角矩阵表示倾斜因子。该分解的几何解释如图3所示，u表示扁平的物体平面，右上方的平行四边形表示摄像机平面，θ，ϕ分别是摄像机的纬度经度，用来表示摄像机的位置，ψ表示摄像机平面的旋转，λ表示放缩倍数，其中θ与公式1中的t t一一对应，t=1/cosθ表示图像的绝对倾斜。

假设u1=u(A(x,y))u1=u(A(x,y)),u2=u(B(x,y))u2=u(B(x,y))表示摄像机在不同视角下得到的两幅图像，其中A,B表示成像过程中的仿射变换，使用公式1可以定义u1到u2的变换如下：

其中τ与两幅图像的绝对倾斜、经度差有关，表示图像之间的相对倾斜，该定义的详细信息请参阅文献[7]。J.M.Morel在该理论的基础上对每一幅图像做仿射变换模拟摄像机位置变化产生的仿射形变提出一种完全仿射不变的匹配算法即ASIFT。本文将简化描述符与ASIFT模拟机制相结合在保证仿射不变的前提下，提高匹配效率，算法具体过程如下：

图3 SVD分解的几何解释

（1）对每一幅图像进行仿射变换模拟由于摄像机位置变化产生的仿射形变。图像的仿射形变主要取决于经纬度的变化，因此在对原始图像做仿射变换时只对摄像机的经纬度进行模拟，为了模拟出尽可能多的形变图像，在对经纬度采样时按照如下规则进行：

a.对纬度采样时保证与之相关的倾斜因子t按照1,a，a2，…，an的规律变化，其中

b.对经度采样时ϕ按照0,b/t，…，kb/t的规律变化，其中b=72∘，k是kb/t<=180∘的最大整数解。

（2）对每一幅模拟图像使用SIFT方法检测特征点，确定主方向，最后使用圆形区域生成简化的32维描述符。

（3）对左右图像的任意一对模拟图像使用最近距离次近距离比算法建立匹配关系如图4所示。最近距离次近距离比算法匹配图像时，计算左图中每个描述符与右图中所有描述符的欧氏距离，如果最近距离和次近距离的比值小于给定的阈值，则两个描述符对应的点匹配成功。最终的匹配结果是所有模拟图像对匹配结果的并集，由于模拟图像模拟了摄像机位置变化产生的各种仿射形变，因此该匹配结果对于图像的仿射变换具有较好的适应性，文献[7]在理论上证明了该方法的仿射不变性。

（4）使用对极几何的约束消除错误匹配，RANSAC（Random Sample Consensus）[8]是剔除错配点常用的方法，然而该方法对于初始匹配点集的依赖性较大，如果初始匹配点集中错误匹配点过多，将无法正确的剔除错配点，ORSA（Optimized RANSAC）[9]是基于 RANSAC改进而来的方法，该方法有效的克服了RANSAC对于初始匹配点集过分依赖的缺陷，本文使用该方法消除错匹配得到最终的匹配结果。

图4 仿射不变匹配算法

2 实验结果与分析

研究人员在ASIFT源代码的基础上对本文算法进行编程实现，为了评价匹配性能，采用Morel图像集[7]对本文算法进行测试，并与ASIFT的匹配性能进行对比。Morel图像集分为绝对倾斜测试集和相对倾斜测试集两部分，绝对倾斜测试集包括一幅油画在放缩倍数为1和10的情况下拍摄的两组图像，以及一本杂志在放缩倍数为4的情况下拍摄的一组图像，相对倾斜测试集包含一本杂志在绝对倾斜为2和4的情况下摄像机经度从零度到九十度逐渐增大拍摄得到的两组图像。

2.1 绝对倾斜实验分析

本文使用放缩倍数为1的图像集进行绝对倾斜实验，将本文方法与ASIFT在匹配点数、匹配速度两个方面对比，实验结果如表1所示，表中各列从左至右一次表示绝对倾斜值得大小，ASIFT匹配点数，本文算法匹配点数，ASIFT匹配速度，本文算法匹配速度，其中匹配速度计算公式如下：

表1 绝对倾斜实验结果

本文算法得到的匹配点数量相对于ASIFT有所减少，平均下降了10%左右。在基于图像局部特征描述符的匹配算法中，选择的描述符对关键点的区分能力越高，关键点的独有特征被描述的越充分最后得到的匹配点的数量就会越多，然而这种描述符的生成过程往往非常复杂，在匹配时的计算量较大。本文为了提高匹配速度，在SIFT描述符的基础上进行简化操作，最后使用32维描述符执行匹配任务，由于降维后的描述符对于关键点的区分能力相对于SIFT描述符有所下降，所以最终匹配点的数量有所减少，但是平均仍然保持在ASIFT 90%左右，最好的情况可以达到96%，从后续的实验结果中可以看到在相对倾斜较大的情况下甚至超过了ASIFT。在使用最近次近距离算法建立匹配关系时，使用本文简化后的描述符代替SIFT描述符计算欧氏距离，每一对描述符的计算次数可以减少64次，所以本文算法执行匹配任务时大大降低了计算量，实验数据表明本文算法的匹配速度平均约为ASIFT的1.5倍。

表2 相对倾斜实验结果

2.2 相对倾斜实验分析

表2记录了相对倾斜图像集上的实验结果，各列含义与表1基本相同，不过此时第一列表示相对倾斜的变化。由表中数据可知，本文算法在绝对倾斜等于2的相对倾斜图像集上得到的匹配点数相对于ASIFT有所减少，匹配速度明显提高与绝对倾斜的实验结果规律一致，但是当绝对倾斜增大至4时，随着图像之间相对倾斜的逐渐增大，本文算法得到的匹配点数超过了ASIFT,尤其是当相对倾斜大于10的时候，该规律非常明显，而且此时的匹配速度平均是ASIFT的6倍左右。随着图像仿射形变的增大，图像上可以检测到的关键点的数量会逐渐减少，而且描述符之间的相似度也会越来越大因此发生错误匹配的概率也会随之增加，另外本文算法使用的简化描述符对不同关键点的区别能力不如SIFT描述符，所以当图像之间的仿射形变较大时本文算法得到的错配点可能会更多。如图7所示，本文算法得到的匹配点数虽然多于ASIFT,但是也引入了更多的错误匹配点。

图5 相对倾斜为14.3的图像对的匹配结果

3 结语

本文针对SIFT描述符维度过高、不具备仿射不变性的缺陷，将简化描述符算法与ASIFT模拟机制相结合提出一种完全仿射不变的图像匹配算法，实验数据表明该算法对于仿射形变较大的图像依然可以稳定工作，而且本文算法的匹配速度明显快于ASIFT。本文算法使用的简化描述符对于图像中关键点的区别能力不如SIFT描述符，在初次匹配结果中引入了更多的重复匹配，增加了去除重复匹配的时间开销，不利于匹配速度的优化，有时甚至导致匹配速度低于ASIFT,相对倾斜为7.7的实验结果便属于此类情况。为了解决该问题，下一步考虑结合核密度估计理论建立图像之间的匹配关系。

[1]David G Lowe,Distinctive Image Features from Scale-Invariant Keypoints,IEEE International Journal of Computer,vol 60,pp.91-110,2004.

[2]Ke Y,Sukthankar R.PCA-SIFT:A More Distinctive Representation for Local Image Descriptors.Proceedings of the 2004 IEEE Computer Society Conference on IEEE,vol.2,2004,pp.506-513.

[3]Z.Zhou,S.Cheng and Z.Li.MDS-SIFT:An Improved SIFT Matching Algorithm Based on MDS Dimensionality Reduction.2016 3rd International Conference on Systems and Informatics（ICSAI）,Shanghai,2016,pp：896-900.

[4]X.Zhou,K.Wang and J.Fu.A Method of SIFT Simplifying and Matching Algorithm Improvement.2016 International Conference on Industrial Informatics-Computing Technology,Intelligent Technology,Industrial Information Integration（ICIICII）,Wuhan,2016,pp.73-77.

[5]Matas J,Chum O,Urban M,et al.Robust Wide-Baseline Stereo from Maximally Stable Extremal Regions[J].Image and Vision Computing,2004,22（10）:761-767.

[6]W.Hu,W.Zhou and J.Guan.A Modified M-SIFT Algorithm for Matching Images with Different Viewing Angle.2016 IEEE International Conference on Signal and Image Processing（ICSIP）,Beijing,2016：247-250.

[7]Morel J M,Yu G.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009,2（2）:438-469.

[8]Fischler M A,Bolles R C.Random Sample Consensus:a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].Communications of the ACM,1981,24（6）:381-395.

[9]Moisan L,Stival B.A Probabilistic Criterion to Detect Rigid Point Matches Between Two Images and Estimate the Fundamental Matrix[J].International Journal of Computer Vision,2004,57（3）:201-218.

[10]Lindeberg T.Scale-Space Theory:A Basic Tool for Analyzing Structures at Different Scales[J].Journal of Applied Statistics,1994,21（1-2）:225-270.

[11]C.Harris and M.Stephens.A Combined Corner and Edge Detector,in Proceedings of the Fourth Alvey Vision Conference,Vol.15,1988：147-151.

[12]K.Mikolajczyk and C.Schmid,Indexing Based on Scale Invariant Interest Points,in Proceedings of the 8th International Conference on Computer Vision（ICCV）,2001：525-531.

[13]K.Mikolajczyk and C.Schmid,Scale and Affine Invariant Interest Point Detectors,Int.J.Comput.Vis.,60（2004）：63-86.

[14]D.Lowe,Distinctive Image Features from Scale-Invariant Key Points,Int.J.Comput.Vis.,60（2004）：91-110.

[15]L.F evrier,A Wide-Baseline Matching Library for Zeno,Internship Report.http://www.di.ens.fr/～fevrier/papers/2007-Internsip ReportILM.pdf（2007）.

[16]K.Mikolajczyk and C.Schmid.An Affine Invariant Interest Point Detector,in Proceedings of the Seventh European Conference on Computer Vision（ECCV）,Springer-Verlag,London,2002：128-142.

[17]K.Mikolajczyk and C.Schmid.A Performance Evaluation of Local Descriptors,in Proceedings of the International Conference on Computer Vision and Pattern Recognition,Vol.2,2003,pp.257–2.