基于KNN和MSR的局部放电模式识别研究
2018-01-24陈敬德孙源文罗林根盛戈皞
陈敬德 李 峰 孙源文 罗林根 盛戈皞
电力设备绝缘故障占电力设备故障的50%以上,电力设备绝缘劣化会产生局部放电现象,而局部放电又会进一步加剧绝缘劣化的程度[1-2],局部放电的模式识别对及时发现绝缘损坏程度和制定有针对性的检修方案有重大意义。局部放电模式识别的研究困难重重,局部放电信号比较微弱,又混叠有场强干扰信号,提取局部放电的特征量非常困难,虽然国内外研究人员在局放模式识别领域作了大量的探索,但当前的局部放电模式识别技术仍难以满足工程实用的要求。
局部放电模式识别包括放电模式的构造、放电特征量的提取以及分类识别。其中放电类型特征量的提取是局部放电模式识别的关键,目前提取信号特征的方法主要有时域分析法和参数统计法。时域分析法的研究对象是局部放电信号的时域波形信号,直接从放电信号的时域波形中提取类型特征,但局部放电信号在传播过程中衰减严重且采集到的时域信号混含噪声信号,提取到的特征量难以对相应的放电类型进行准确表征,所以该方法的可重复性较差。统计分析法是认可度相对较高的局部放电特征提取方法,它的特点是利用统计参数记录局部放电信号的特征,比时域分析法的抗干扰性强。
目前,提取局部放电信号特征参数的方法主要有PRPD谱图法、波形特征参数法、小波分析理论法、放电统计参数法以及分形理论法。PRPD图谱法是目前比较受重视的局部放电模式识别方法,该方法以放电量q和放电相位φ 与放电次数n之间的关系 Hn(q,φ)作三维图谱来描述不同的局放类型的特征。文献[3]采用三维谱图提取放电指纹特征,并用人工神经网络作为局放类型识别算法。文献[4]提出了基于PRPD谱图,采用统计算子偏斜度、陡峭度和不对称度等作为识别的特征参量,该方法是当前使用较为广泛的局部放电特征提取办法。然而放电量q在很大程度上受电压值、试品电容大小、耦合电容大小等很多因素的影响,故基于PRPD图谱的局放模式识别方法可重复性较差。另一方面,很多情况下测量局部放电信号时没有同步获取相位信息,且直流系统的局部放电并无相位,PRPD谱图法在直流设备局部放电和无相位信息的放电序列中是不适用的。放电统计参数法将局部放电现象看作一个随机过程,该方法对局部放电的放电量、放电脉冲幅值以及放电相位等进行统计学分析,研究其是否符合某种特定的统计分布。近年来的研究表明,局部放电的脉冲幅值的分布可以用 weibull分布来表达,且不同的放电类型,其weibull分布参数不同,以此作为局部放电类型识别的特征量。文献[5-7]研究了weibull分布在放电信号类型识别领域的应用,文献[5]的研究表明,单故障的放电脉冲的高度可以用两参数的 weibull来表征,且吻合度较高,基于weibull分布参数的局部放电识别取得了不错的效果,然而该算法对多故障放电信号识别性能较差,且抗干扰性不强。
近年来,随着大数据技术的发展,随机矩阵理论因其具备处理大量数据的能力而引起了学者们的注意。随机矩阵的主要特征是以随机变量为元素,随机矩阵谱分布理论主要研究在特定条件下随机矩阵的特征根的分布情况[8-10]。随机矩阵理论的提出源于物理学研究,随后在无线通信、基因统计、网络安全、图像处理、核物理、金融网络、统计学等领域得到很好的应用[11-16]。已有学者将高维随机矩阵用于输变电设备关键性能的评估和状态监测数据的异常检测,见文献[17]和文献[18]。本文则尝试将大维随机矩阵理论用于局放模式识别中,提出了一种针对局部放电时域信号的基于高维随机矩阵谱分布的局部放电模式识别技术,文中设计了4种局部放电实验模型:悬浮电极放电、气隙放电、高压沿面放电、电晕放电。利用放电模型产生的局放信号来构造高维随机矩阵,运用时间序列在随机矩阵下的谱分布理论,将每种放电信号所构成矩阵的特征根分布特性作为知识库,提出了基于K-近邻(KNN)算法的局部放电模式识别方法。实验结果表明,基于随机矩阵理论的局放模式识别方法具有较高的可行性及研究价值。
1 随机矩阵圆环率理论
对矩阵的乘积Z 其中Xi是N×n独立同分布的非厄米特随机方阵 X˜i的奇异值等价矩阵,则Z的经验谱密度将收敛于[19-20]:
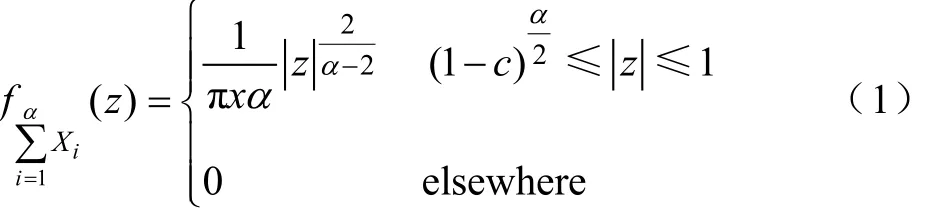
当 N , n→∞和 c=N/n≤ 1时,在复平面表示下,特征根将处于内圆半径为 ( 1 - c )α/2外圆半径为1的圆环内。
2 放电模式特征量的选取
2.1 PD信号的高维随机矩阵构造
针对 PD信号构建高维随机矩阵,可以利用单位时间间隔Δt的数据向量来生成矩阵X,其表达式如式(2)所示,数据生成方式如图1所示。
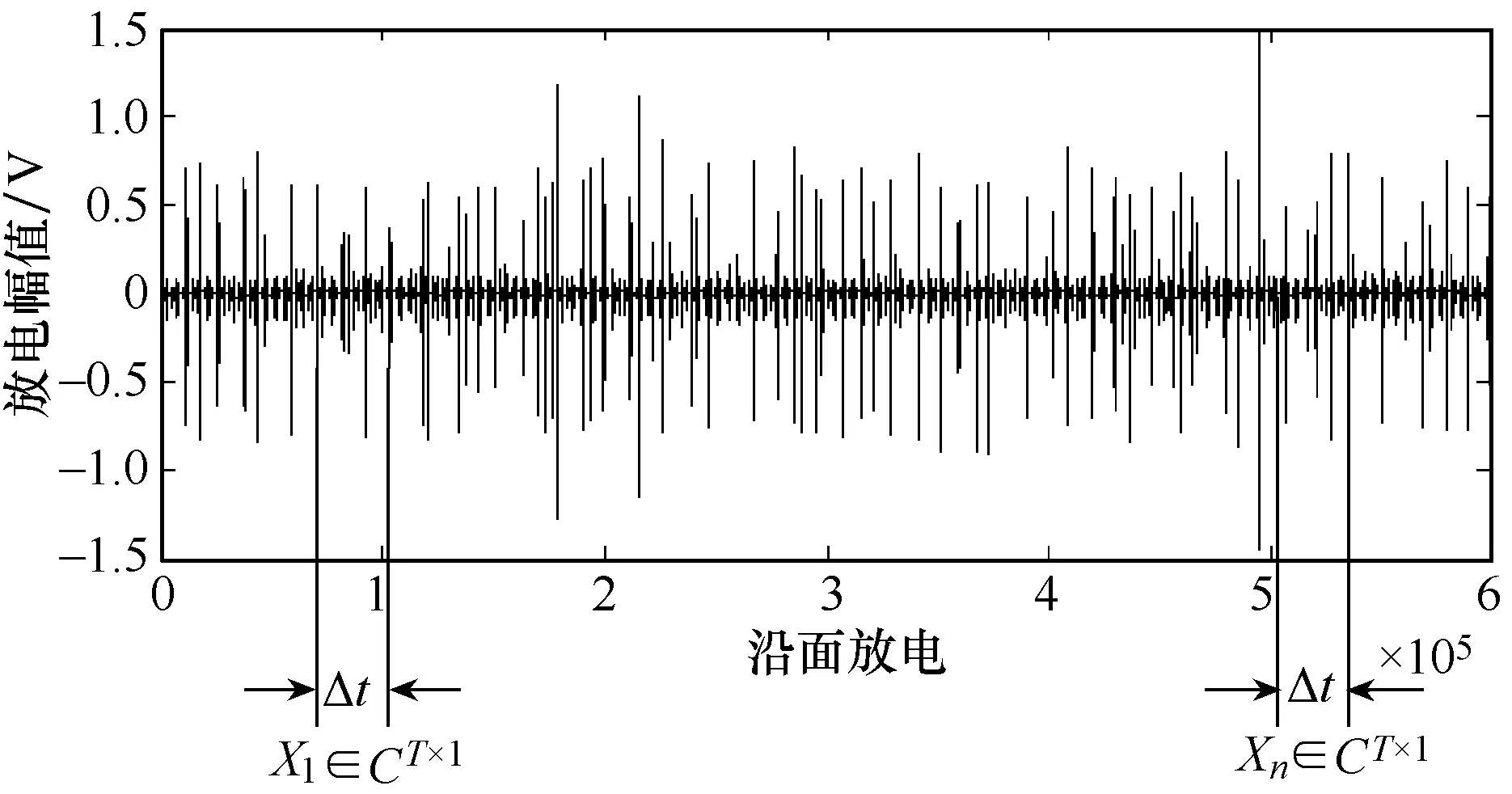
图1 PD信号的高维随机矩阵构造

X是 TN× 随机矩阵,可以通过改变采样频率和采样时长来调整矩阵X的行列数比值,以保证矩阵X满足随机矩阵理论分析的要求。
局部放电波形与绝缘缺陷类型紧密相关,本文设计了4种典型的局部放电模型,如图2所示。
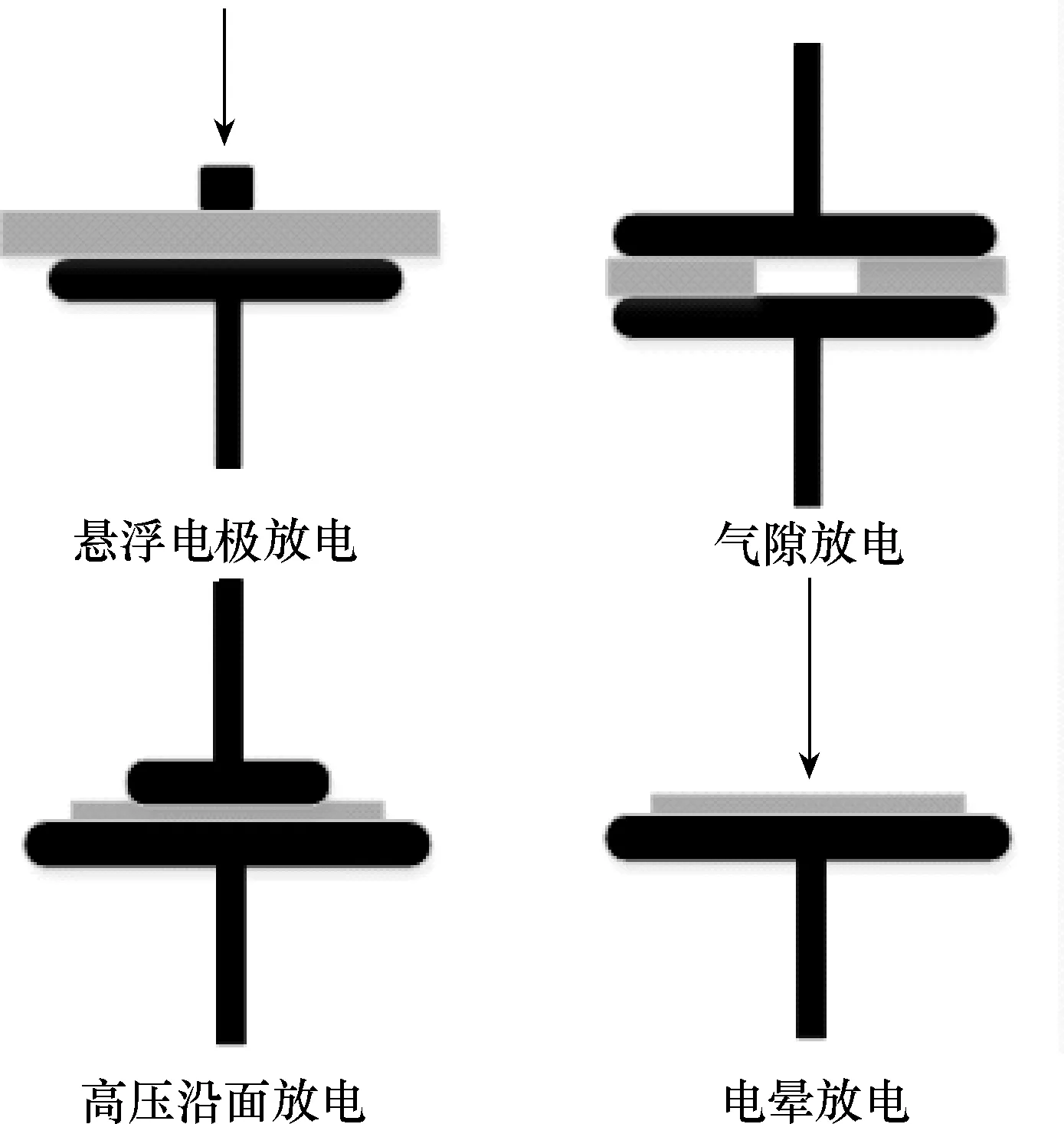
图2 几种典型的放电模型结构
2.2 局放模式识别的特征量选取
从前面的理论分析知,由 PD信号产生的时间序列,构造满足一定要求的高维矩阵,理论上已证明其特征根呈环状分布。本文拟将这个特性选作局部放电模式识别的特征量。利用放电模型产生4种局放信号,并采集相应的特高频信号各10组,本实验利用放电信号的多脉冲波形进行谱分析,利用示波器的顺序采集模式可以得到放电信号的多脉冲波形,所谓多脉冲波形即为采集多个脉冲且只对放电脉冲附近若干点进行采集,示波器的设置为(500mV/div,200ns,1G/S,顺序采集模式,300段脉冲),在此设置下,每个脉冲采集了 2000×10-9s×1G/s=2000个点,一个完整的多脉冲波形共采集了300×2000=600000个点,按式(2)构造每种局部放电特高频信号的600×1000维随机矩阵X。
图3给出了一组4类放电信号所生产高维矩阵Z的特征根谱分布情况,从图中可看出其特征根很明显呈现圆环分布的特点,且每个圆环的内径大小不同,环内的谱分布疏密也有自身的特点,故可选取四类放电波形的谱分布圆环的平均谱半径(mean spectral radius, MSR)为放电类型识别的特征量[21]:
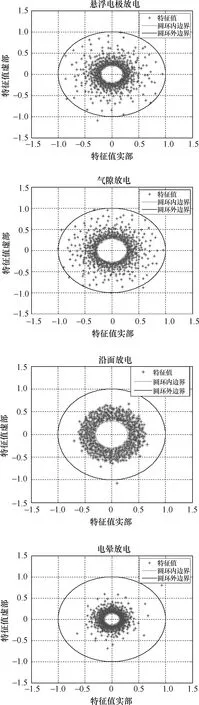
图3 四类放电信号波形的谱分布圆环

3 基于KNN和MSR的识别方法
电缆终端的安装工艺不当可能会引起绝缘油受潮。K近邻算法是一种简单的机器学习算法[22],即给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类。K值的选择,距离度量和分类决策规则是该算法的3个基本要素。距离度量在本实验中选择欧氏距离,即对于任意两类信号的10个波形的圆环谱分布,其MSR的欧式距离为 d (κ1iMSR, κ2iMSR):

本实验中的分类决策规则为对于新输入波形的MSR,在60个波形(每类局放信号各十个波形)的谱分布知识库中挑出与其最近的K个MSR,然后看这K个MSR多数属于哪一类,则把新输入的波形归为该类局放信号。本实验结果表明,当K取3时,识别效果最好。
4 实验验证
4.1 验证该方法的可行性
分别采集每类放电波形50个,构造相应的高维随机矩阵进行谱分析,并将提取的特征量输入训练好的K-近邻识别算法进行识别,对各种放电波形的识别率见表1。
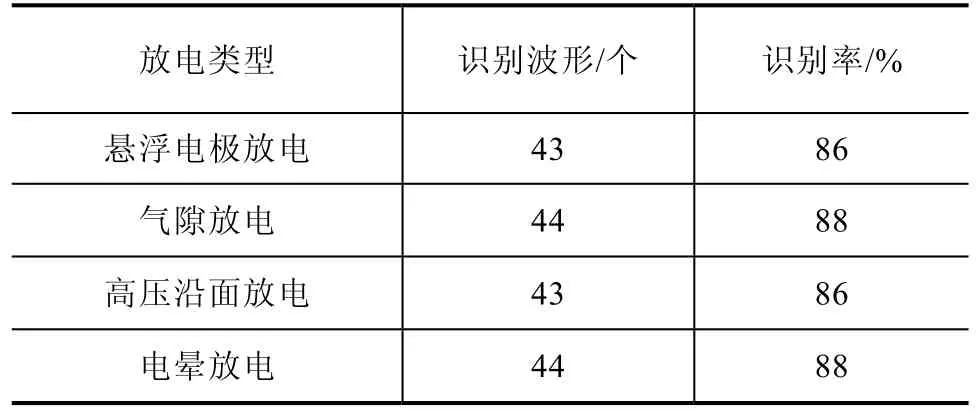
表1 基于KNN和MSR的局部放电模式识别方法对4类放电波形的识别结果
由实验结果可知,基于KNN和MSR的局部放电模式识别方法对4种放电信号的识别率较高,均在85%以上。实验结果证明了基于高维随机矩阵谱分布的局部放电模式识别方法的有效性。
4.2 实验结果分析
实验过程中发现,在采集同一类放电信号时,示波器触发时刻的不同,采集到的放电信号的幅值序列也有明显的不同,如图4所示的9个电晕放电波形。但基于随机矩阵谱分析方法仍发现这类信号波形的特征值分布具有明显的聚类特点。这说明基于随机矩阵谱分布的局放模式识别方法具有很好的稳定性,抗干扰性较强。
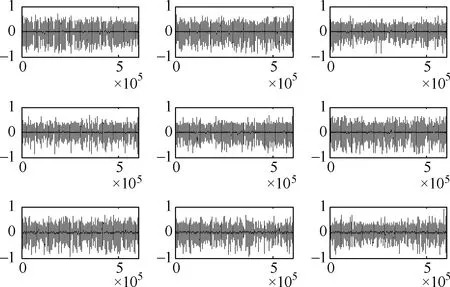
图4 电晕放电多脉冲波形
5 结论
以 PD信号时间序列构造的高维随机矩阵的特征根分布特性作为 PD模式识别的特征量,相较于传统的以脉冲波形或脉冲峰峰值为特征量的识别方法,因其采集的数据量较大(具有一定的大数据特性)和分析机理不同,受波形时间序列的干扰影响较小,算法简单且稳定性高,具有工程实用性和研究价值。后序将研究不同背景噪声下,同一种类型的放电信号所构造矩阵的谱分布规律,进而构建更加完备的知识库,将有助于增加本文方法的鲁棒性和普适性。
[1] 侯慧娟. 基于电磁波天线阵列的变电站局部放电信号处理及定位方法[D]. 上海: 上海交通大学,2014.
[2] 侯慧娟, 盛戈皞, 苗培青, 等. 基于超高频电磁波的变电站局部放电空间定位[J]. 高电压技术, 2012,38(6): 1334-1340.
[3] 姜磊, 朱德恒, 李福祺, 等. 根据三维谱图识别变压器绝缘典型模型放电的研究[J]. 电机与控制学报,1999(4): 215-218.
[4] Gulski E, Kreuger F H. Computer-aided Recognition of Discharge Sources[J]. IEEE Transactions on Electrical Insulation, 1992, 27(1): 82-92.
[5] Contin A, Montanari G C, Ferraro C. PD source recognition by Weibull processing of pulse height distributions[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(1): 48-58.
[6] 胡文堂, 高胜友, 余绍峰, 等. 统计参数在变压器局部放电模式识别中的应用[J]. 高电压技术, 2009,35(2): 277-281.
[7] 唐炬, 王静, 李剑, 等. 统计参数用于局部放电模式识别的研究[J]. 高电压技术, 2002, 28(8): 4-6, 37.
[8] Wigner E P. Characteristic vectors of bordered matrices with infinite dimensions i[M]//The Collected Works of Eugene Paul Wigner. Springer Berlin Heidelberg, 1993: 524-540.
[9] Wigner E P. On the distribution of the Roots of certain symmetric matrices[J]. Annals of Mathematics, 1958,67(2): 325-327.
[10] Adamczak R. On the Marchenko-Pastur and circular laws for some classes of random matrices with dependent entries[J]. Electronic Journal of Probability,2011, 16(16): 1068-1095.
[11] org.cambridge.ebooks.online.book.Author@badf.Random Matrix Methods for Wireless Communications[Z].
[12] 王磊, 郑宝玉, 崔景伍. 随机矩阵理论与无线通信[J]. 南京邮电大学学报(自然科学版), 2010, 30(3):90-96.
[13] 韩华, 吴翎燕, 宋宁宁. 基于随机矩阵的金融网络模型[J]. 物理学报, 2014(13): 1.
[14] 刘佳, 金德鹏, 张文铸, 等. 基于随机矩阵理论的链路流量监测[J]. 清华大学学报:自然科学版, 2010(1):117-120.
[15] Bai Zhidong, Jiang Dandan, Yao Jianfeng, et al.Corrections to LRT on Large-dimensional Covariance Matrix by RMT[J]. Annals of Statistics, 2009, 37(6B):3822-3840.
[16] 陈健. 基于随机矩阵理论的层次聚类方法在基因网络研究中的应用[D]. 湘潭: 湘潭大学, 2009.
[17] 严英杰, 盛戈皞, 王辉, 等. 基于高维随机矩阵大数据分析模型的输变电设备关键性能评估方法[J]. 中国电机工程学报, 2016(2): 435-445.
[18] 魏大千, 王波, 刘涤尘, 等. 高维随机矩阵描述下的量测大数据建模与异常数据检测方法[J]. 中国电机工程学报, 2015(S1): 59-66.
[19] Tao T. Topics in random matrix theory[M]. New York:American Mathematical Society, 2012.
[20] Guionnet A, Krishnapur M, Zeitouni O. The single ring theorem[J]. Annals of Mathematics, 2011, 174(2):1189-1217.
[21] Xu Xinyi, He Xing, Ai Qian, et al. A correlation analysis method for power systems based on random matrix theory[J]. IEEE Transactions on Smart Grid,2017, 8(4): 1811-1820.
[22] 杨丽华, 戴齐, 郭艳军. KNN文本分类算法研究[J].微计算机信息, 2006, 22(21): 269-270, 185.
